Non-digital computing: neuromorphic applications and mathematical theory
An old quest taking a fresh turn
The world-transforming powers of Turing / digital computing need no explanation. Yet, alternative paradigms of “computing” have been proposed in waves and cycles since the beginnings of the computing era, some short-lived, others more enduring. The graphics below gives an impression of the diversity in names, ideas, communities (and PR wizards, too).

Some niches and quantum computing excepted, academic impact and industrial involvement has been ephemeral.
This has started to change. Two major motivations to re-inspect and re-invest in non-digital computing are that
- physical ceilings for CMOS based digital microchip technologies are coming into sight (“End of Moore’s Law”),
- the ever-growing energy hunger of digital infrastructure is becoming insupportable.
Specifically, considerable and considerably fast growing efforts are now being spent on innovative “neuromorphic” (wide sense) approaches. The international conference Cognitive Computing: Merging Concepts with Hardware funded by the Volkswagen Foundation and co-organized by Jaeger in 2018 gives a good overview of the interdisciplinary span of non-digital computing research.
Optical and neuromorphic reservoir computing at MINDS
Due to its leading role in reservoir computing, MINDS has naturally been pulled first into optical, then additionally into neuromorphic hardware manifestations of reservoir computing, and finally, into nonstandard hardware research in general. Besides EU project reviewing and holding tutorials, we co-organized
- the workshop Technology and Architectures Development for Brain Inspired Integrated Circuits (at ESSCIRC - ESSDERC 2016),
- the conference Dynamical Systems and Brain Inspired Computing (ULB Brussels, June 2017),
- the workshop Dynamical Systems and Brain-inspired Information Processing (October 2017, Univ. Konstanz, Germany)
- the conference Cognitive Computing: Merging Concepts with Hardware, a flagship event of the Volkswagen Foundation (Dec 2018).
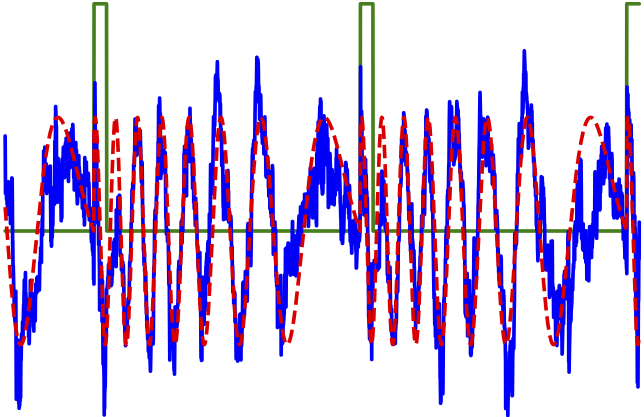
In our own research, we have been busy and will be busy realizing spiking recurrent neural computing on analog microprocessors of the DYNAP family, within the EU H2020 project NeurRAM3 (completed, 2016-2019) and the ongoing EU H2020 project MemScales. The challenges lie in the combination of extremely low numerical precision, stochastic dynamics, device mismatch and unobservability of core physical system parameters. Image: Shaping and stabilizing the dynamics of a spiking recurrent neural network, in a not quite trivial multi-timescale task. Solved challenge: adaptable synaptic weights only had 1.6 bit precision. Green: input signal, red: target output, blue: network output signal.
Publication on using non-digital neuromorphic hardware: X. He, T. Liu, F. Hadaeghi, H. Jaeger (2019): Reservoir Transfer on Analog Neuromorphic Hardware. Int. IEEE EMBS Conf. on Neural Engineering (NER '19) (pdf )
Mathematical foundations of non-digital computing
For a computer scientist, the answer to the question, “what is computing”, is given with magnificent authority by the formal model of Turing computability.
But, Turing computability hardly looks like the right model for understanding brains or other unconventional physical materials and media. Modelers must pick their tools from a scattered range of options, including
- dynamical systems theory (with dozens of subfields),
- stochastic processes (with dozens of subfields),
- statistical physics (with dozens of subfields),
- analytical and algebraic geometry and topology (with dozens of subfields).
A coherent mathematical foundation for non-digital computing, which could step into the supremely unifying role that Turing computability has served for digital computing, is missing. In a tutorial talk delivered at the Beyond von-Neumann Computing: Computing meets Nanophysics Leopoldina Symposium (2017), Herbert Jaeger explores the history of “computing” concepts and works out challenges for future formalizations (slides).
Research at MINDS has always been inclined towards mathematical theory. Our main contributions to mathematical formalizations of information processing systems (wide sense) are
- observable operator models and conceptors, two mathematical modeling paradigms which clarify fundamental properties of stochastic and high-dimensional nonlinear dynamics, respectively; and have immediate bearing on the design of novel learning algorithms;
- a unification of existing concepts of attractors in input-driven dynamical systems, relevant for “computing” because attractor concepts are often invoked as a link to explain discrete symbols in continuous dynamics (G. Manjunath, H. Jaeger (2014): The Dynamics of Random Difference Equations is Remodeled by Closed Relations. SIAM Journal on Mathematical Analysis 46(1), 459-483 (pdf);
- and finally (and currently, foremostly) we collaborate with materials scientists, mathematicians, theoretical computer scientists and researchers from the wider unconventional computing fields to lay the foundations for a generalized theory of computing (H. Jaeger (2021): Toward a Generalized Theory Comprising Digital, Neuromorphic, and Unconventional Computing. Neuromorphic Computing and Engineering 1(1) open access)
