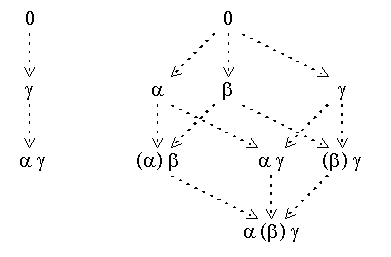
Title Abstract Contents 1 2 3 4 5 Acknowlegments References Footnotes
In this section, some example argumentation theories are discussed. They are used to compare the admissible set and the argumentation stage approach. We make use of diagrams, which show all admissible sets and argumentation stages of a theory. It turns out that the diagrams of the stages of a theory can be interpreted as diagrams of the process of argumentation. As a result, they are called argumentation diagrams.[8]
The argumentation theory ({alfa, beta, gamma}, {(beta, alfa), (gamma, beta)}) is an example of a counterattack: one argument, alfa, is challenged by another, beta, which is itself challenged by a third argument, gamma.
Figure 2 shows on the left side a diagram of the admissible sets of the theory, and on the right side a diagram of the argumentation stages. Each node corresponds to an admissible set or an argumentation stage. The arrows represent inclusion (for admissible sets) or inclusion of range (for stages). An admissible set is denoted by listing its elements; a stage is denoted by listing the arguments in its range and putting its defeated arguments in brackets. (The 0 indicates the empty list of arguments.)
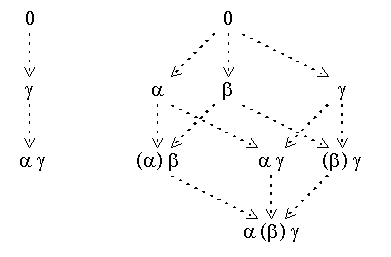
Figure 2: Counterattack and reinstatement
The canonical stages of the admissible sets {}, {gamma} and {alfa, gamma} are ({}, {}), ({gamma}, {beta}) and ({alfa, gamma}, {beta}), respectively. For this theory, the unique preferred stage ({alfa, gamma}, {beta}) coincides with the (complete) stage extension.
Whereas the diagram on the left has no clear intuitive interpretation (except for set theoretical inclusion of admissible sets), the diagram of the argumentation stages on the right can be interpreted as a diagram of the process of argumentation, in the sense that each path in the diagram corresponds to a line of argumentation, in which the arguments of the theory are taken into account in a particular order.
In that interpretation, each arrow indicates that a new argument is taken into account. Arrows with the same direction correspond to the same argument that is taken into account. For instance, the arrows between the stages ({}, {}) and ({beta}, {}) and between ({alfa, gamma}, {}) and ({alfa, gamma}, {beta}) both indicate that the argument beta is taken into account. Different paths through the diagram from the initial stage ({}, {}) to the final stage ({alfa, gamma}, {beta}) correspond to different orders in which the arguments are taken into account.
Of course the status of arguments can change. This theory has a line of argumentation in which alfa is reinstated: In the line of argumentation ({alfa}, {}), ({beta}, {alfa}), ({alfa, gamma}, {beta}), in which first alfa, then beta, and finally gamma is taken into account, the argument alfa is first undefeated, then defeated, and finally undefeated again.
The argumentation theory ({alfa, beta}, {(beta, alfa), (alfa, beta)}) is an example of mutual attack: the arguments alfa and beta challenge each other. As a result, the theory has multiple extensions. The stage extensions of the theory are ({alfa}, {beta}) and ({beta}, {alfa}). Figure 3 shows the corresponding diagrams of admissible sets and argumentation stages. Multiple extensions with equal range are separated by a comma.
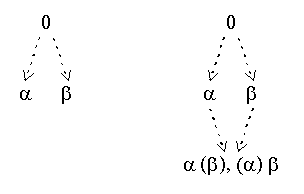
Figure 3: Mutual attack and multiple extensions
The argumentation theory ({alfa, beta, gamma}, {(beta, alfa), (alfa, beta), (gamma, alfa)}) has an additional argument gamma, that challenges the argument alfa. As a result, the theory has multiple stages, ({alfa}, {beta}) and ({beta}, {alfa}). The theory shows that a theory with multiple stages does not always have multiple stage extensions. Its unique stage extension is ({beta, gamma}, {alfa}). As a result, the notion of multiple stages is a proper generalization of the notion of multiple extensions. Figure 4 shows the corresponding diagrams of admissible sets and argumentation stages of the argumentation theory.
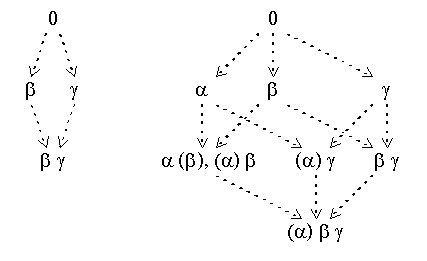
Figure 4: Multiple stages, but no multiple extensions
Clearly, multiple non-extension stages have no counterpart in the admissible set approach.
The argumentation theory ({alfa1, alfa2, alfa3}, {(alfa1, alfa2), (alfa2, alfa3), (alfa3, alfa1)}) contains a loop of attacks: the argument alfa1 challenges the argument alfa2, which challenges alfa3, which on its turn challenges alfa1. This theory gives an example of admissible stage extensions (and preferred stages) that are not stage extensions. The unique admissible stage extension of this theory is ({}, {}). The stage extensions are ({alfa1}, {alfa2}), ({alfa2}, {alfa3}) and ({alfa3}, {alfa1}). The theory has no complete stage extension (or, equivalently, stable extension). In Figure 5, this is indicated by the three question marks ???.
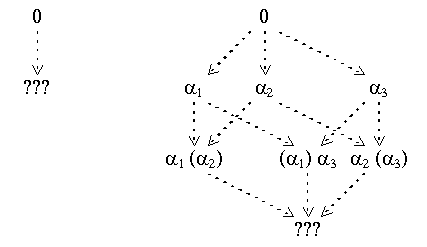
Figure 5: Loop of attacks and non-admissible stage extensions
The diagram of the argumentation stages shows that any two of the arguments of the theory can be taken into account, but that it is impossible to take all three of them into account.
The example generalizes to loops of attacks of any odd number of arguments. It is essential that the number of arguments in the loop is odd. An even number results in two extensions of equal range.
The ornate title of this section refers to the argumentation theory ({alfa, beta, gamma1, gamma2, gamma3}, {(alfa, beta), (beta, alfa), (gamma1, gamma2), (gamma2, gamma3), (gamma3, gamma1), (alfa, gamma1)}). It consists of the mutually attacking arguments alfa and beta, one of which, alfa, breaks the loop of attacks of the arguments gamma1, gamma2 and gamma3. This theory shows that preferred stages are not always admissible stage extensions. It has two preferred stages: ({beta}, {alfa}) and ({alfa, gamma2}, {beta, gamma1, gamma3}). The range of the first is smaller than that of the second. Only the second is an admissible stage extension, that is even complete. Figure 6 shows on the left all admissible sets of the theory, and on the right only the canonical admissible stages (and their twins, i.e., stages with equal range).
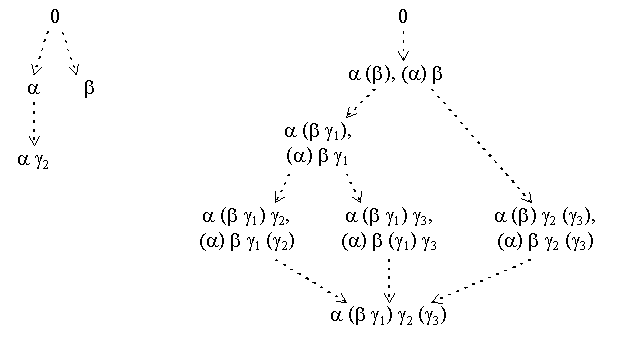
Figure 6: Mutual attack skewly breaking a loop of attacks [9]
In a sense, an admissible stage extension is better than a preferred stage with smaller range, since more arguments are taken into account. It is therefore 'better informed'.
The argumentation theory ({alfai | i = 0, 1, 2, ...}, {(alfai, alfaj) | i > j}) has no stage extension. The stages ({alfai}, {alfaj | i > j}), for i = 0, 1, 2, ..., are the only canonical stages of the theory. Their ranges exhaust the arguments of the theory, but the stages are mutually not compatible. Compatibility is defined as follows: Stages Stage1 = (UndefeatedArgs1, DefeatedArgs1) and Stage2 = (UndefeatedArgs2, DefeatedArgs2) are compatible if UndefeatedArgs1 contains no elements of Challenged(UndefeatedArgs2) and UndefeatedArgs2 contains no elements of Challenged(UndefeatedArgs1).[10] It can be shown that a theory has a stage extension if and only if there is a sequence of compatible stages that exhaust all arguments of the theory.
The theory has one admissible set, its preferred extension {}. Figure 7 shows the admissible sets and the canonical stages.
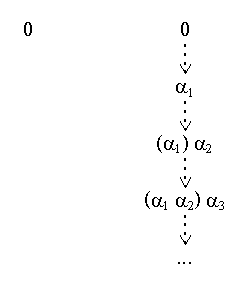
Figure 7: No exhausting sequence of compatible stages
Even though the theory has no stage extension, its canonical stages provide more information than its admissible sets.
Title Abstract Contents 1 2 3 4 5 Acknowlegments References Footnotes