Title Abstract Contents 1 2 3 4 5 Acknowlegments References Footnotes
In this section, we investigate the connections between the admissible set and the argumentation stage approach. The following notation is used.
Challenging(Args) = {Arg | There is a defeater (Arg, Arg') with Arg' in Args}
Challenged(Args) = {Arg | There is a defeater (Arg', Arg) with Arg' in Args}
The following lemma reformulates some of the definitions in terms of these sets.
(1) An argument Arg is acceptable with respect to a set of arguments Args if and only if Challenging({Arg}) is a subset of Challenged(Args).
(2) For any set of arguments Args the following are equivalent:
(i) Args is conflict-free.
(ii) Args contains no element of Challenged(Args).
(iii) Args contains no element of Challenging(Args).
(3) A set of arguments Args is admissible if and only if it is conflict-free and Challenging(Args) is a subset of Challenged(Args).
(4) A defeat status assignment (UndefeatedArgs, DefeatedArgs) is an argumentation stage if and only if UndefeatedArgs contains no elements of Challenged(UndefeatedArgs) and DefeatedArgs is a subset of Challenged(UndefeatedArgs).
Admissible sets of arguments are closely related to the sets of undefeated arguments of an argumentation stage. However, not all such sets are admissible. For instance, ({alfa}, {}) is a stage of the argumentation theory ({alfa, beta}, {(beta, alfa)}), while {alfa} is not admissible. The following result characterizes when the undefeated arguments of a stage form an admissible set and which stages have the same admissible set as set of undefeated arguments.
(1) For any argumentation stage (UndefeatedArgs, DefeatedArgs) the following holds:
UndefeatedArgs is admissible if and only if Challenging(Args) is a subset of DefeatedArgs.
(2) For any admissible set AdmissibleArgs the following holds:
(AdmissibleArgs, DefeatedArgs) is an argumentation stage if and only if DefeatedArgs is a subset of Challenged(AdmissibleArgs).
Proof: (1) First notice that the set of undefeated arguments of an argumentation stage is conflict-free. Then the result follows from the lemma. (2) Follows from the lemma.
A consequence of the second part of the theorem is that any admissible set occurs as the set of undefeated arguments of an argumentation stage. In particular, if AdmissibleArgs is an admissible set of arguments, then (AdmissibleArgs, {}) and (AdmissibleArgs, Challenged(AdmissibleArgs)) are argumentation stages.
The following theorem characterizes admissible sets of arguments in terms of stages.
A set of arguments Args is admissible if and only if (Args, Challenging(Args) v Challenged(Args)) is an argumentation stage.
Proof: First notice that from the second part of the lemma it follows that a set of arguments Args is conflict-free if and only if (Args, Challenging(Args) v Challenged(Args)) is a defeat status assignment. The 'only if'-part follows from the third part of the lemma and the second part of theorem 1. The 'if'-part follows from the first part of theorem 1.
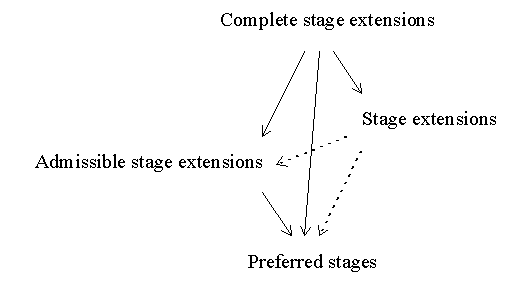
A stage with an admissible set of undefeated arguments is an admissible stage. Stages of the form (Args, Challenged(Args)) are canonical stages, since they have maximal range among the stages with a particular set of undefeated arguments. So, if Args is admissible, (Args, Challenging(Args) v Challenged(Args)) is a canonical stage. An admissible stage with maximal range (which is always canonical) is an admissible stage extension.
Admissible stage extensions do not correspond to stage extensions, since stage extensions are not necessarily admissible stages. For instance, the theory ({alfa1, alfa2, alfa3}, {(alfa1, alfa2), (alfa2, alfa3), (alfa3, alfa1)}) has the stage ({}, {}) as unique admissible stage extension, and the non-admissible stage extensions ({alfa1}, {alfa2}), ({alfa2}, {alfa3}) and ({alfa3}, {alfa1}) as stage extensions (see section 4.3). This example shows that neither all admissible stage extensions are stage extensions, nor vice versa. In a sense, however, admissible stage extensions are 'smaller' than stage extensions, since the range of any admissible stage extension is smaller than (or equal to) the range of any stage extension.
One might expect that admissible stage extensions correspond to Dung's preferred extensions. This is however not true, since there can be canonical stages with a preferred extension as set of undefeated arguments that are not admissible stage extensions. For instance, the theory ({alfa, beta, gamma1, gamma2, gamma3}, {(alfa, beta), (beta, alfa), (gamma1, gamma2), (gamma2, gamma3), (gamma3, gamma1), (alfa, gamma1)}) has the (canonical) admissible stages ({beta}, {alfa}) and ({alfa, gamma2}, {beta, gamma1, gamma3}). The range of the first is a proper subset of the second, while both {beta} and {alfa, gamma2} are preferred extensions (see section 4.4).
The following corollary characterizes Dung's preferred extensions in terms of stages.
A set of arguments Args is a preferred extension if and only if (Args, Challenging(Args) v Challenged(Args)) is an admissible stage with maximal set of undefeated arguments.
Proof: Follows immediately from theorem 2 and the observation that Challenging and Challenged are monotonic operators.
Canonical stages with a preferred extension as set of undefeated arguments, as in corollary 1, are preferred stages. Admissible stage extensions are preferred stages, but not vice versa, as we have seen.
Dung's stable extensions and our complete stage extensions coincide, however, as the following corollary shows.
A set of arguments Args is a stable extension if and only if (Args, Challenging(Args) v Challenged(Args)) is a complete stage extension.
The relations between the discussed types of stages are summarized in Figure 1. The continuous arrows indicate conceptual inclusion. We have given counterexamples for all missing arrows. Stage extensions and admissible stage extensions have no counterpart in Dung's paper (1995). The dotted arrows indicate that any stage extension has a range larger than (or equal to) the range of any admissible stage extension or preferred stage.
Figure 1: Relations between types of argumentation stages
The previous results have shown that the argumentation stages of a theory generalize the admissible sets of that theory. In these results, the argumentation theory was fixed. The section ends with a comparison result that says that the argumentation stages of a theory correspond exactly to the admissible sets of certain other theories. The following notation is used.
For an argumentation theory (Arguments, Defeaters) and a set of arguments Range, the restriction of the theory to Range, denoted (Arguments, Defeaters)|Range = (Arguments|Range, Defeaters|Range), is defined as follows:
Arguments|Range = Range
Defeaters|Range = {(Arg, Arg') in Defeaters | Arg and Arg' are elements of Range}
Theorem 3 is based on the observation that for an argumentation stage a defeater is only relevant if its challenging and challenged argument are both taken into account, i.e. are elements of the range of the stage.[7] The theorem follows straightforwardly from the definitions of admissible sets and argumentation stages. It shows that the argumentation stage approach is the 'local' version of the 'global' admissible set approach.
(UndefeatedArgs, DefeatedArgs) is an argumentation stage with range Range of the argumentation theory (Arguments, Defeaters) if and only if UndefeatedArgs is admissible with respect to the theory (Arguments, Defeaters)|Range.
Clearly, the set of undefeated arguments of an argumentation stage is in fact a stable extension of the restricted theory.
Title Abstract Contents 1 2 3 4 5 Acknowlegments References Footnotes