informatie   rooster   hoorcollege   practicum   links

Signaalanalyse - tijd-frequentievlak

Dit onderdeel gaat over het beschrijven van signalen die als functie van de tijd van frequentieinhoud veranderen, ofwel: niet-stationaire signalen. Centraal hierbij is de vraag:

Op welk tijdstip en bij welke frequenties wordt energie uitgezonden?

Het tijd-frequentievlak is het domein waarin de de ontwikkeling van de expressie van energie op bepaalde frequenties in de vorm van een zogenaamd spectrogram kan worden gevisualiseerd.

Niet-stationaire signalen

Tot nu hebben ons beperkt tot signalen van N-opeenvolgende punten (typisch N tijdstappen) in de ontwikkeling van een signaal. In de praktijk ontwikkelen signalen zich en willen we N niet precies even lang als het gehele signaal kiezen, maar de temporele ontwikkeling van de frequentieinhoud van een signaal volgen (een stationair signaal kan immers maar heel weinig informatie vertegenwoordigen) door N veel kleiner dan de totale signaallengte te kiezen en steeds op een ander deel van het signaal "in te zoomen". In goed Nederlands heet dit een "venster" (op het signaal), maar in het jargon een window.

Stel dat we de eerste 4096=2.^12 punten (het woord "nul" van het tijddomeinsignaal nul123.wav grafisch weergeven.

[x, fs] = wavread('nul123.wav'); % Inlezen signaal x
strips(x(1:4000), 0.1, fs); % Afbeelden in strips van 0.1 sec
title('Golfvorm van "nul"')
xlabel('Tijd in sec');
ylabel('Amplitude');

Dit ziet er zo uit (het tijdsignaal volgen alsof je leest).

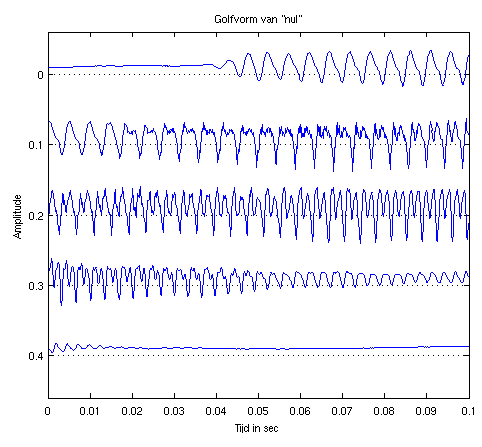
Rond sample t = 0.040 s = 40 ms begint de /n/. Rond sample t = 120 ms is er een vrij duidelijke overgang, waarbij ineens veel meer fijnstruktuur (en dus hogere frequenties) zichtbaar worden. Dit is de overgang naar de /u/. Hierna treden nog een aantal relatief langzame kwalitatieve veranderingen op in het signaal voor het signaal rond sample 3300 weer stationair wordt. Het is duidelijk dat de frequentieinhoud gedurende de tijd verandert. De vraag is hoe we dit zo goed mogelijk zichtbaar kunnen maken, ofwel:

Wat is de ontwikkeling van de frequentiebijdragen is als functie van de tijd?
Hoe is de energie verdeeld over het tijd-frequentievlak?

Spectogram

Wat we zouden kunnen doen is de tijdas verdelen in korte stukjes (vensters of windows genaamd) en die transformeren en visualiseren. Hiervoor bestaat een Matlab functie specgram.m, maar omdat de niet bijzonder inzichtelijk is, is een alternatief geschreven: fftGram.m. de matlab helpfunctie geeft via help fftGram:

  fftGram - Berekend en plot Fourierspectrogram (in dB) van inputvector
 
  [S, SInfo]=fftGram(x, fs, nfft, stepT, windowName, PLOT)
  
    x          - inputvector
    fs         - sample frequentie in Hz
    nfft       - dimensie van fft input vector
    stepT      - stapgrootte in ms (tijdverschil tussen opvolgende
                 output vectoren)
    windowName - wijze waarop fft-input vector geisoleerd is uit x. 
                 Keuze uit: {'rectangular','hamming','triangle',
                 'hanning'}
    PLOT       - al of niet plotten, waarde >1 wordt als dynamisch
                 bereik in dB geinterpreteerd
    
    S          - Spectrogram lineair (niet in dB)
    SInfo =    - Informatie over S              
           fs  - Sample frequentie
     T_window  - Tijdsduur in ms waarmee nfft overeenkomt
      delta_f  - Frequentieverschil tusse opvolgende basisvectoren
                 (fs/nfft)
        stepT  - Stapgrootte stepT
            F  - Vector met de frequenties van basisvectoren
            T  - Vector met de corresponderende tijden van het midden
                 van de outputvectoren
    

Het enige nieuwe in deze functie is de diversiteit aan manieren om een tijdwindow te "isoleren" uit het totale signaal x. Een eenvoudig window krijg je via xw = x(1:128), waarbij (de eerste) 128 punten geselecteerd worden. Dit heet een rechthoekig (rectangular) window. Om redenen die later onderzocht zullen worden (zie het practicum over spectrogrammen) is het doorgaans verstandiger om xw te vormen door x zodanig met een window-functie w puntsgewijs te vermenigvuldigen zodat gegarandeerd wordt dat de waarden van xw = x.*w bij het begin en eind klein zijn (of zelfs 0 zijn). We zullen in eerst instantie een zogenaamd "Hanning window" (weer jargon, de officiële naam is 'von Hann' window) gebruiken.

De kern van fftGram.m bestaat uit een loop waarbij voor elk window x(range).*w (waarbij range steeds stepT ms verschoven wordt in de tijd) het energiespectrum X wordt uitgerekend en toegevoegd als kolom ii in de spectrogram matrix S.
N.B. Een spectrum is een vector van frequenties S(f), een spectrogram is een matrix met als indices frequentie en tijd S(f,t).

    stepSamp = fs*(stepT/1000);
    maxFr = floor((length(x)-nfft)./stepSamp);
    S = zeros(nfft/2, maxFr);
    for ii = 1:maxFr
      range = (ii-1)*stepSamp + [1:nfft];
      X = abs(fft(fftshift(x(range).*w)).^2);
      S(:,ii) = X(1:nfft/2);
    end
    

Met fftGram is het mogelijk om de frequentieontwikkeling in de tijd weer te geven. We kunnen hiermee bijvoorbeeld de energieverdeling in het tijd-frequentievlak voor t = 0 en t = 0.5 sec en voor f = 0 tot f = 4000 Hz weergeven:

[S SInfo] = fftGram(x(1:4000), fs, 128, 5, 'hann, nfft=128, Twindow=16', 60);
colorbar

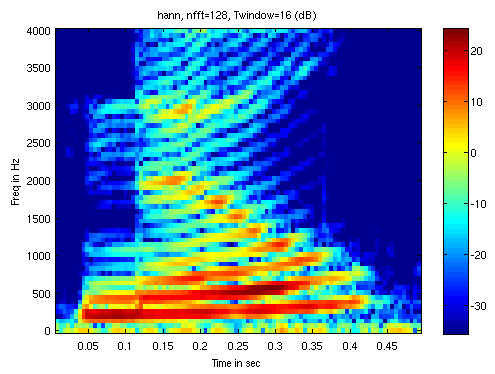
Dit plaatje geeft van de eerste 4000 samples (0.5 s) van x, gesampled op 8000 Hz , met behulp van een 128-dimensionale FFT (dus nfft/2+1 = 65 verschillende basisvectoren), elke 10 ms het Fourierspectrum op basis van een "Hanning window". Alle Fourierspectra zijn achter elkaar gezet zodat ze een 2-dimensionale matrix vormen waarvan de waarden via een dB-schaal op een dynamisch bereik van 60 dB via de Matlab imagesc functie zijn afgebeeld. De kleurcodering komt overeen met de energie, de laagste waarden zijn -60 dB (een factor miljoen) lager dan het maximum.

We zullen later dieper ingaan op wat er inhoudelijk precies te zien is in bovenstaande figuur. Voor nu volstaat het met op te merken dat de min of meer horizontale structuren de harmonischen (d.w.z. de grondtoon en de boventonen daarvan) van het woord "nul" zijn.

Trade-off temporele en frequentie resolutie

Laten we eens kijken wat er gebeurt wanneer we de dimensionaliteit (en daarmee de duur van de gewindowde input) van de FT veranderen:

subplot(2,2,1)
[S_512 SInfo_512] = fftGram(x(1:4000),fs,512,5,'hann, nfft=512, Twindow=64',60);
colorbar
subplot(2,2,2)
[S_256 SInfo_256] = fftGram(x(1:4000),fs,256,5,'hann, nfft=256, Twindow=32',60);
colorbar
subplot(2,2,3)
[S_128 SInfo_128] = fftGram(x(1:4000),fs,128,5,'hann, nfft=128, Twindow=16',60);
colorbar
subplot(2,2,4)
[S_64 SInfo_64] = fftGram(x(1:4000),fs,64,5,'hann, nfft=64, Twindow=8',60);
colorbar

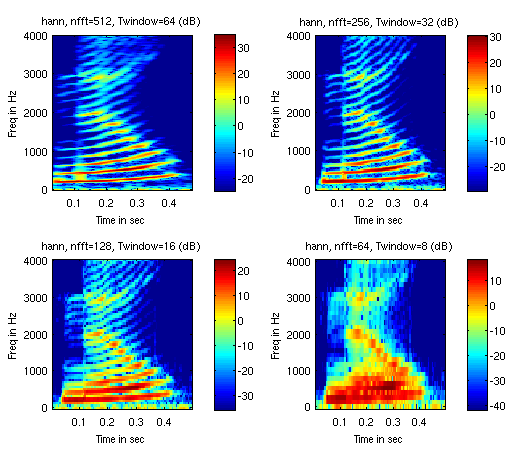
Door de dimensionaliteit van de inputvector te verlagen werd de windowgrootte van 64 ms gereduceerd tot 8 ms, em tegelijkertijd werd het aantal frequentiekanalen om het te signaal in het frequentiedomein mee te beschrijven gereduceerd van 257 (via 129 en 65) tot 33 (steeds nfft/2+1). Bij een windowgrootte van 8 ms is het frequentie-oplossend vermogen van de FT terug gebracht tot fs/N = 8000/64 = 125 Hz, onvoldoende om in dit geval (d.w.z. met dit window) de individuele harmonischen zichtbaar te maken. Aan de andere kant lijkt het temporeel-oplossendvermogen juist groter; in horizontale richting zijn veranderingen veel sneller en abrupter dan in de situatie linksboven met T = 64 ms. We kunnen dit wat nauwkeuriger bekijken met:

subplot(3,1,1)
[S_512 SInfo_512] = fftGram(x(1:4000),fs,512,5,'hann, nfft=512, Twindow=64',60);
xlabel(''); axis([0 .5 0 4000])
line([0.04 0.04], [0 4000], 'color', 'red')
subplot(3,1,3)
[S_64 SInfo_64] = fftGram(x(1:4000),fs,64,5,'hann, nfft=64, Twindow=8',60);
axis([0 .5 0 4000])
line([0.04 0.04],[0 4000],'color','red')
subplot(3,1,2);
plot(linspace(0,4000/fs, 4000), x(1:4000))
title('Golfvorm')
line([0.04 0.04],[-1 1],'color','red')
line(SInfo_512.T(1) + SInfo_512.T_window/1000/2*[-1 1],[.5 .5],'color','green')
line(SInfo_64.T(1) + SInfo_64.T_window/1000/2*[-1 1],-[.5 .5],'color','black')

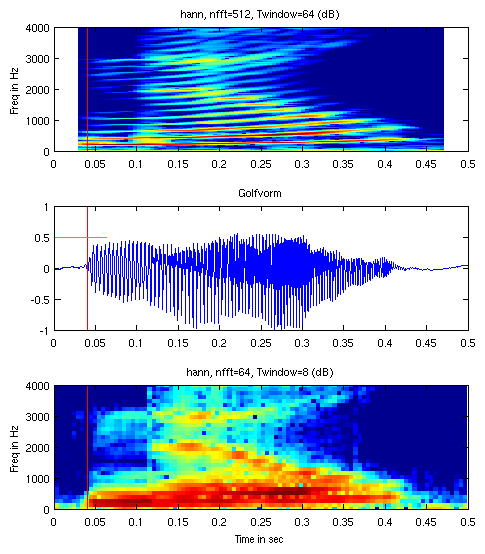
In de middelste subplot is de golfvorm weergegeven. Rond de rode lijn bij t = 0.040 s = 40 ms start de /n/ van nul. In het onderste plaatje (waar de windowgrootte 8 ms is) valt dit precies samen met de start van een energierijke bijdrage rond 200 Hz. In het bovenste plaatje echter, zijn de eerste harmonischen al gestart in het eerste frame. Dit is logisch want in deze situatie is de duur van elk window 64 ms. Het eerste window is in het groen weergegeven in het tijddomein plaatje. Wanneer een signaal op t = 40 ms start omvat het laatste derde deel van het eerste window al een deel van het signaal. Omdat de tijdas in de beide frequentiespectra overeenkomt met de positie van het midden van het inputwindow correspondeert het eerste window met t = 32 ms in het bovenste spectrogram en t = 4 ms in het onderste spectrogram.

Het is duidelijk in het bovenste plaatje is het frequentieoplossendvermogen groot, maar de temporele resolutie klein, in het onderste plaatje is de situatie omgekeerd: de temporele resolutie is groot, maar de frequentieresolutie klein. Dit is logisch want het frequentieverschil df = fs/N tussen de basisvectoren neemt af wanneer het aantal Fourier-basisvectoren groter wordt. Hierdoor neemt de frequentieresolutie toe. Naarmate de inputdimensie (de duur in samples) van de input toeneemt wordt het window waarover de FT iets zegt echter groter. Er geldt:

    df = fs/N = 1/(N*dt) = 1/T_window      % want dt=1/fs
    

Ofwel:

    df * T_window = 1 
    

Windowen

Waar we tot nu toe geen aandacht aan hebben besteed is aan de gevolgen van het windowen (het proces om een deel van het signaal te isoleren van de rest van het signaal om er een Fouriertransformatie op los te kunnen laten). Het belang van windowen komt aan bod in het practicum, voor dit moment richten we de aandacht op het feit dat een window (dus elke manier om een subsignaal te isoleren) een effectieve breedte/duur heeft. Van een aantal veel gebruikte en bekende windows kunnen we dit visualiseren.

N = 200;
t = linspace(0,3,3*N);
x = cos(2*pi*5*t);

subplot(2,2,1);
w = [zeros(1,N) rectwin(N)' zeros(1,N)];
plot(t,x,'-g',t,x.*w, 'r', t, w, 'b')
axis([0 3 -1.1 1.1])
title(['Rechthoekig - eff. breedte: ' num2str(mean(rectwin(N)),'%0.3f')])

subplot(2,2,2);
w = [zeros(1,N) triang(N)' zeros(1,N)];
plot(t,x,'-g',t,x.*w, 'r', t, w, 'b')
axis([0 3 -1.1 1.1])
title(['Driekoekig - eff. breedte: ' num2str(mean(triang(N)),'%0.3f')])

subplot(2,2,3);
w = [zeros(1,N) hanning(N)' zeros(1,N)];
plot(t,x,'-g',t,x.*w, 'r', t, w, 'b')
axis([0 3 -1.1 1.1])
title(['Hanning - eff. breedte: ' num2str(mean(hanning(N)),'%0.3f')])

subplot(2,2,4);
w = [zeros(1,N) hamming(N)' zeros(1,N)];
plot(t,x,'-g',t,x.*w, 'r', t, w, 'b')
axis([0 3 -1.1 1.1])
title(['Hamming - eff. breedte: ' num2str(mean(hamming(N)),'%0.3f')])

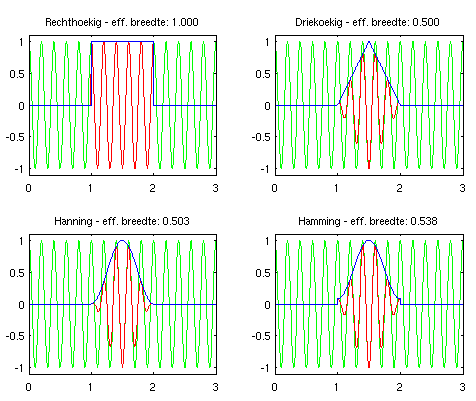
In het groen is het signaal x weergegeven dat per tijdseenheid 5 keer oscilleert. In het blauw is een window functie weergegeven die, vermenigvuldigd met x, in rood een nieuw signaal xw = x.*w oplevert. In dit geval zorgt het window voor een signaal xw dat overal buiten het bereik [1,2] nul is en daarbinnen ongelijk aan nul kan zijn. De eenvoudigste manier om een window te maken is door het bereik [1,2] onveranderd door te laten en alles er buiten op nul te zetten. De toepassing van dit "rechthoekige" window is in de figuur linksboven te zien. Het rode signaal laat zien dat, in dit geval (door de keuze van de cosinus-functie voor x) het gewindowde signaal op t = 1 van 0 naar 1 springt om daarna 5 perioden de cosinus te volgen en op t = 2 weer van 1 naar 0 te springen. Het op deze wijze gewindowde signaal geeft een discontinuïteit die redelijk dramatische gevolgen kan hebben voor het resultaat van de Fouriertransformatie. (Dit wordt in het practicum onderzocht).

De overige drie windows hebben geen (Hanning window en het driehoekig window) of minder (Hamming window) afkapeffecten, maar betalen daarvoor doordat de windows gebeurtenissen nabij de rand minder laten meetellen en daardoor een kleinere effectieve breedte hebben. Wordt de breedte van het rechthoekig window op 1 gezet dan de zijn de andere windows daar slechts de helft van. Met andere woorden, de effectieve duur van het window T_effectief is kleiner dan de volledige duur T_window. Via

    df * T_window = 1     % afgeleid in de vorige paragraaf
    

Geldt dus ook dat de effectieve breedte df_effectief = 1/T_effectief van de FT-basisvector bijdragen toeneemt.