

De Fouriertransformatie stelt ons in staat om van het tijddomein naar het frequentiedomein te gaan. Dat transformeren klinkt wellicht geheimzinnig, maar het komt er op neer dat er meerdere methoden zijn om de input te beschrijven. Transformeren is niets anders dan het signaal te beschrijven met een andere verzameling "basiseenheden" dan eerst het geval was.
Het omrekenen van "inch", "feet", "yard" en "mile" eenheden naar centimeters, meters en kilometers is een zelfde soort "transformatie" (in dit geval van Engelse basiseenheden naar SI-eenheden) als de Fourier transformatie. Bij een transformatie stel je je de vraag: "Hoeveel van elk van de nieuwe eenheden (km, m, en cm) zitten er in input (b.v. 3 mile, 195 yards, 3 feet, 8 inch)?"
Het blijkt mogelijk te zijn een signaal op een groot aantal verschillende manieren te beschrijven (te transformeren) door het kiezen van basisvectoren. Voor het ene doel is de ene verzameling basisvectoren geschikter, voor het andere doel een andere. Hier zullen we ons beperken tot de een verzameling pulsen (voor het tijddomein) en een verzameling sinus- en cosinusfuncties (voor het frequentiedomein).
De pulsen zijn geschikt om de temporele ontwikkeling van het signaal nauwkeurig te volgen, de sinus- en cosinusfuncties vertellen je over de periodiciteiteigenschappen van het signaal.
De wiskunde die nodig is om de Fouriertransformatie te begrijpen
is beperkt tot de definities van de sinus en de cosinus en de
basis van de vectormeetkunde; In het bijzonder het inproduct en
hoe het inproduct te interpreteren is als projectie van een vector
op een andere vector: xp = (x.p) * p
Omdat we ons hier beperken tot het "transformeren" van rijtjes discrete getallen (en niet een continue input) wordt hier de zogenaamde Discrete Fouriertransformatie (DFT) besproken. Qua eigenschappen komt die sterk overeen met de continue variant die vooral van wiskundig belang is. Bij computertoepassingen wordt alleen de discrete variant gebruikt, en dan vooral de Fast Fourier Transform (FFT): een hele slimme en efficiënte implementatie van de DFT op basis van complexe getallen. Op basis van een paar regels is het gebruik hiervan vrij eenvoudig.
basis 1: pulsen
In het tijddomein wordt het signaal beschreven als een serie
pulsen, waarbij van elke puls weergegeven wordt hoe die puls
meegewogen moet worden. Wanneer bn een functie is die op tijdstip
n een puls genereert is b2 = [0 1 0 0]. De tijdreeks [1 0 -1 0] is
dan te beschrijven als:
[1 0 -1 0] = 1*b1 + 0*b2 + (-1)*b3 + 0*b4
Of in een plaatje:
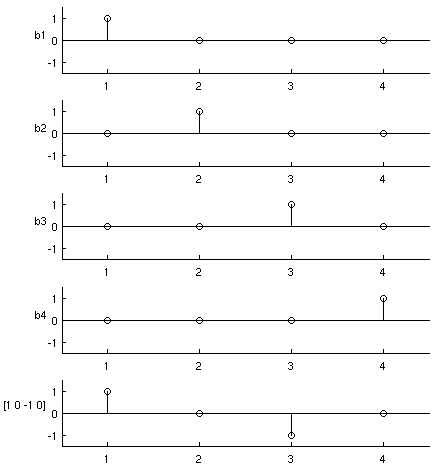
De functies bn worden basisvectoren (of
basisfuncties) genoemd wanneer geldt dat het inproduct (de som van
de vermenigvuldiging van identieke indexen van twee gelijksoortige
vectoren) van een basisvector met zichzelf 1 is en met all andere
basisvectoren 0. Ofwel:
bn·bm = 0 wanneer n ongelijk is aan m
bn·bm = 1 wanneer n gelijk is aan m
Bijvoorbeeld:
b2·b3 = sum([0 1 0 0] .* [0 0 1 0]) = sum([0 0 0 0]) = 0
b2·b2 = sum([0 1 0 0] .* [0 1 0 0]) = sum([0 1 0 0]) = 1
Deze eigenschap betekent dat b2 en b3
loodrecht op elkaar staan en ook dat ze ongecorreleerd zijn in de
zin dat een puls op tijdstip 2 niets zegt over tijdstip 3 en ook
niet over alle andere tijdstippen anders dan n = 2.
Er zijn altijd precies evenveel basisvectoren als de dimensie (d.w.z. het aantal indexen of, zoals hier, tijdstappen) van de vector die beschreven moet worden. Een volledige basis van de vierdimensionale inputvector wordt dus gevormd door {b1, b2, b3, b4}.
Een andere eis aan een basisvector is dat zijn lengte altijd 1 is. Dit houdt in dat het inproduct van een basisvector met zichzelf altijd 1 moet zijn. Voor pulsen als baisvectoren is makkelijk te zien dat aan deze eis wordt voldaan.
Een set basisvectoren waarmee alle vectoren kunnen worden beschreven heet een volledige basis, als ze ook nog eens loodrecht op elkaar staan (inproduct nul) heet het ook wel een orthogonale basis, zijn dan ook nog eens de lengtes 1 dan heet het een orthonormale basis. Een bekende volledige orthonormale basis is bijv. de basis van vectoren van lengte 1 langs resp, x, y en z as die zo het cartesisch coordinaten stelsel vormen.
basis 2: cosinus- en sinusfuncties
De tijdreeks [1 0 -1 0] uit de vorige paragraaf lijkt ook wat op
een cosinus-functie. Er is een cosinus-functie die deze
opeenvolging van waarden ook kan aannemen. Namelijk:
[1 0 -1 0] = cos(2*pi * [0 1 2 3]/4 * 1)
= cos(2*pi * [0 0.25 0.5 0.75])
= cos(ω1)
Hierin is cos(ω1) een afkorting voor een
cosinus-functie die (in dit geval in 4 tijdstappen) 1 periode van
de cosinusfunctie omvat (de reden dat de vermenigvuldiging met 1
expliciet weergegeven is). De bijbehorende sinusreeks
sin(ω1) ziet er zo uit:
[0 1 0 -1] = sin(2*pi * [1 2 3 4]/4 * 1)
= sin(2*pi * [0 0.25 0.5 0.75])
= sin(ω1)
Ondanks het feit dat ze dezelfde frequentie hebben, is het
inproduct van de cos(ω1) en
sin(ω1) is gelijk aan 0. Immers:
cos(ω1)·sin(ω1) = sum( [1 0 -1 0] .* [0 1 0 -1]) = 0
Beide functies staan dus loodrecht op elkaar (en zijn dus
onafhankelijk, ongecorreleerd). Het inproduct van
sin(ω1) en sin(ω1) met
zichzelf is echter nog niet precies 1.
cos(ω1)·cos(ω1) = sum([1 0 -1 0] .* [1 0 -1 0])
= sum([1 0 1 0]) = 2 = sqrt(2) * sqrt(2)
sin(ω1)·sin(ω1) = sum([0 1 0 -1] .* [0 1 0 -1])
= sum([0 1 0 1]) = 2 = sqrt(2) * sqrt(2)
Door de basisvectoren te delen door de norm sqrt(2)
kan het inproduct met zichzelf wel gelijk aan 1 gemaakt worden. Om
de basis volledig te maken zijn nog twee extra basis functies
nodig. Hiervoor kan gekozen worden voor:
[1 1 1 1] = cos(2*pi* [0 1 2 3]/4 * 0)
= cos(2*pi* [0 0 0 0])
= cos(ω0)
[1 -1 1 -1] = cos(2*pi* [0 1 2 3]/4 * 2)
= cos(2*pi* [0 .5 1 1.5])
= cos(ω2)
Waarbij cos(ω0) verwijst naar een
cosinus-functie die 0 keer oscilleert (dus constant is) en
cos(ω2) verwijst naar een functie die precies 2
perioden omvat. Ze staan in ieder geval loodrecht op de andere
twee basisfuncties. Bijvoorbeeld:
cos(ω0)·sin(ω1) = sum( [1 1 1 1] .* [0 1 0 -1]) = sum([0 1 0 -1]) = 0
cos(ω2)·sin(ω1) = sum( [1 -1 1 -1] .* [0 1 0 -1]) = sum([0 -1 0 1]) = 0
De bijbehorende sinus-functies, sin(ω0) en
sin(ω2) zijn weinig zinvol, wanneer de cosinus 1
of -1 is zijn de bijbehorende sinus waarden altijd 0. De
"sinus-basisvectoren" zijn dus [0 0 0 0] en niet zinvol om iets
mee te beschrijven.
N.B. Dit argument geldt uitsluitend bij strikt reële
input. Zoals we later zien blijkt dat voor een complex getal
c = a + ib = a * cos(x) + i*b*sin(x) geldt dat de
sinus component correleert met het imaginaire deel.
Voor een volledig basis B = {B1,B2,B3,B4} in het
frequentiedomein geldt (waarbij N de norm is):
B1 = 1/N * cos(ω0) = 1/sqrt(4) * cos(ω0) = [1 1 1 1] / sqrt(4)
B2 = 2/N * cos(ω1) = 1/sqrt(2) * cos(ω1) = [1 0 -1 0] / sqrt(2)
B3 = 2/N * sin(ω1) = 1/sqrt(2) * sin(ω1) = [0 1 0 -1] / sqrt(2)
B4 = 1/N * cos(ω2) = 1/sqrt(4) * cos(ω2) = [1 -1 1 -1] / sqrt(4)
Het tijddomeinsignaal [1 0 -1 0] wordt beschreven met
pulsen p(n) als basisvectoren. In het
frequentiedomein wordt het signaal beschreven als bijdragen van
cosinus en sinus basisvectoren (die in tegenstelling tot pulsen de
gehele lengte van het signaal omvatten). Omdat het signaal
[1 0 -1 0] al precies beschreven wordt door
cos(ω1) en de andere basisvectoren hier
loodrecht op staan, zullen de bijdragen van de andere
frequentiedomeinbijdragen 0 zijn. De beschrijving van het signaal
ziet er (afgezien van het feit dat de cosinus- en
sinusbasisvectoren nog niet genormaliseerd zijn) in de beide
domeinen zo uit.
| domein: | tijd | frequentie |
| basis: | {p1,p2,p3,p4} | {cos(ω0),cos(ω1),sin(ω1),cos(ω2)} |
| beschrijving: | [1 0 -1 0] | [0 1 0 0] |
transformeren
Het is gebruikelijk om signalen in het tijddomein aan te geven met
kleine letters en die in het frequentiedomein weer te geven met
hoofdletters. Stel dat we het tijddomein signaal s = [2 -1 0
-1] willen transformeren tot het frequentiedomein signaal
S. Zoals aan het begin van dit document is gezegd is
het transformeren niets anders dan het afbeelden van een signaal
op een bepaalde verzameling basisvectoren. De bijdrage van een
basisvector aan het beschrijven van een signaal (d.w.z. de
projectie van de signaalvecor op de basisvector) kan berekend
worden met het inproduct. Voor de bijdragen van de puls
basisvectoren in het tijddomein geldt:
s1 = s·b1 = sum([2 -1 0 -1] .* [1 0 0 0]) = 2
s2 = s·b2 = sum([2 -1 0 -1] .* [0 1 0 0]) = -1
s3 = s·b3 = sum([2 -1 0 -1] .* [0 0 1 0]) = 0
s4 = s·b4 = sum([2 -1 0 -1] .* [0 0 0 1]) = -1
En geheel analoog voor de bijdragen van de cosinus/sinus basisvectoren van het frequentiedomein geldt:
S1 = s·B1 = sum([2 -1 0 -1] .* [1 1 1 1]/sqrt(4)) = 0
S2 = s·B2 = sum([2 -1 0 -1] .* [1 0 -1 0]/sqrt(2)) = 2/sqrt(2) = sqrt(2)
S3 = s·B3 = sum([2 -1 0 -1] .* [0 1 0 -1]/sqrt(2)) = 0
S4 = s·B4 = sum([2 -1 0 -1] .* [1 -1 1 -1]/sqrt(4)) = 2
De Fouriertransformatie van het tijddomeinsignaal s = [2 -1
0 -1] is dus S = [0 sqrt(2) 0 2]. Immers, als
de tweede en de vierde Fourierbasisvector (met 1 gewogen) opgeteld
worden, wordt s weer gevonden:
s = S2 * B2 + S4 * B4
= sqrt(2) * [1 0 -1 0] / sqrt(2) + 2 * [1 -1 1 -1] /sqrt(4)
= [2 -1 0 -1]
Dit is de Fouriertranformatie met een 4-dimensionale input die
gegeneraliseerd kan worden tot N dimensies.
In het tijddomein is de verzameling basisvectoren nu dus een
verzameling van N opeenvolgende pulsen. In het frequentiedomein
bestaat de verzameling van N (controleer dit)
basisvectoren uit:
cos(ω0): een basisvector met allemaal
identieke waarden sqrt(1/N)cos(ωk) en sin(ωk): elk
ook basisvectoren met als inproduct met zichzelf de waarde
sqrt(1/(N/2)) die overeenkomen met cosinus- of
sinusbijdragen die over de lengte van de inputvector
k volledige periodes vertonen.cos(ωN/2) vertegenwoordigt de component
met de hoogst mogelijke frequentie. De vector lijkt op
cos(ω0), maar alterneert tussen positieve en
negatieve waarden.
Samen zijn dit N basisvectoren bestaande uit 2
basisvectoren voor cosinusbijdragen van de laagste en hoogste
frequentie en N-2 = 2 * (N./2-1) basisvectoren voor
de frequenties er tussen, waarbij zowel de sinus als de cosinus
nodig is. De hoogste frequentie correspondeert met Nmax =
N/2 perioden.
Voor "perioden" k = 0 : N/2 geldt:
k = 0 | k = 1 : N/2-1 | k = 1 : N/2-1 | k = N/2 |
cos(ω0) / sqrt(N) |
cos(ωk) / sqrt(N/2) |
sin(ωk) / sqrt(N/2) |
cos(ωN/2) / sqrt(N) |
In de noemer staat steeds een maat voor de "lengte" van de vector in de teller, en heeft de vorm van de wortel van het inproduct van de teller met zichzelf (zodat het inproduct met zichzef altijd precies 1 is).
Om de Fouriertransformatie tot N dimensies te
generaliseren en tegelijkertijd de schrijfwijze te vereenvoudigen
kunnen we gebruik maken van de matrixvermenigvuldiging. Bij een
matrixvermenigvuldiging I * J = C geldt immers dat
matrixelementen C(i,j) worden bepaald door het
inproduct van rij i van matrix I en
kolom j van matrix J. Eerst maken we een
NxN-matrix B met daarin in elke kolom een basisvector
Bn (tot nu toe als rijvector geschreven). Vervolgens
schrijven we inputvector s als rijvector (zoals
boven), met als resultaat:
S = [s·B1 s·B2 ... s·BN] = s*[B1 B2 ... BN] = s*B
Hierbij is * een matrixvermenigvuldiging tussen de 1xN-matrix
s en de NxN-matrix B. Het resultaat is
weer een 1xN matrix S (bij matrixvermenigvuldigingen
geldt altijd dat de vermenigvuldiging van AxB-matrix met een
BxC-matrix een AxC-matrix oplevert, ofwel [AxB] * [BxC] =
[AxC]).
Voor de terugtransformatie geldt dat elke tijdindex onstaat door
de som van de bijdragen van alle frequentiedomein basisvectoren
bij die tijdindex. Wanneer we in de matrix B kijken
zien we dat die informatie juist in de rijen aanwezig is (immers
het n-de element per basisvector in het
frequentiedomein verwijst naar het n-de
tijdstip). Voor de terugtransformatie moeten we de rijen en de
kolommen van de matrix B dus omdraaien. Met andere woorden, we
moeten de getransponeerde van B (= B')
nemen. Dus
s = S*B'
Check dit voor het 4-dimesionale voorbeeld!
Samengevat geldt voor de heen en terug (inverse) transformatie:
S = s*B "Heen: tijd -> frequentie"
s = S*B' "Terug: frequentie -> tijd"
Hierbij is B een NxN-dimensionale matrix met in elke
kolom een basisvector. Zowel s als S
zijn rijmatrices.
Bovenstaande formules gelden voor elke transformatie van de ene
basis naar de andere basis. De Fouriertransformatie waarbij van
een basis van pulsen {b} naar een basis
{B} van cosinus- en sinusfuncties wordt
getransformeerd is slechts één voorbeeld van een
transformatie. Het is bijvoorbeeld ook mogelijk (en helemaal niet
moeilijk) om een verzameling basisvectoren te maken die uit louter
cosinusfuncties bestaat. Kies daarvoor {cos(ωk)} met
k = 0, 0.5, 1, 1.5, 2, ..., N/2. Je kunt met
symmetrieargumenten gemakkelijk checken dat hierbij voldaan wordt
aan de eisen voor basisvectoren. De
bijbehorende transformatie heet (zoals te verwachten) de
cosinustransformatie en wordt gebruikt in de automatische
spraakherkenning bij het berekenen van zogenaamde MFCC's
(Mel-scaled Frequency Cepstral Coefficients).
De complexe Fouriertransformatie is een generalisatie naar het
complexe vlak van de strikt reële Fouriertransformatie zoals
die hierboven is beschreven. Hierbij wordt gebruik gemaakt van de
uitdrukkingen: exp(iφ) = cos(φ) +
isin(φ) en exp(-iφ) = cos(φ) -
isin(φ) om sinus- en cosinusfuncties te koppelen aan
complexe e-machten. Dit heeft allemaal wiskundige voordelen die nu
niet van belang zijn, maar die gebruikt worden bij de FFT om de
transformatie efficiënter te kunnen berekenen dan mogelijk is
met behulp van het stukgewijs afbeelden op basisvectoren (zoals
hierboven gebeurde). Omdat de complexe Fourier-transformatie de
norm is (en als de functie fft.m standaard in Matlab
wordt meegelevert) is het belangrijk om te weten welke delen van
de complexe Fouriertransformatie relevant zijn bij het verwerken
van strikt reële input (zoals geluid).
Bij de complexe Fouriertransformatie zijn de basisvectoren
geordend volgens het aantal perioden k per
basisvector (k wordt het golfgetal genoemd). De
basisvectoren zijn:
exp(iωk) = cos(ωk) + isin(ωk), waarbij k=0:N-1.
Hierin zit weer de combinatie van sinus en cosinus vectoren, zoals
boven. Het enige verschil is dat de sinuscomponenten met
i = sqrt(-1) vermenigvuldigd zijn en dat de
k niet van 0 tot N/2 loopt zoals in de
tabel met de basisvectoren, maar van 0 tot
N-1 (dus N verschillende waarden).
De output van een complexe FT op een reële input
x(n) is dus een reeks van N complexe
getallen. Hiervan correspondeert de eerste helft precies met de
basisvectoren in de tabel. Laten we (in Matlab) een 8-dimensionale
vector x van 8 reële random getallen vormen en
die via een FFT transformeren tot X volgens:
x = rand(8,1); % 8-dim vector van random (reële) getallen
X = fft(x); % FT van x (8-dim complexe getallen)
Hieronder zijn x, de periodiciteit k,
het reële en het imaginaire deel van X en de
bijbehorende basisvectoren cos(ωk) en
sin(ωk) weergegeven.
x k X = fft(x) basisvectoren
real(X) imag(X) cos sin
--------------------------------------------------------
0.9501 0 4.4025 0 cos(ω0) sin(ω0)=0
0.2311 1 -0.6472 -0.1055 cos(ω1) sin(ω1)
0.6068 2 0.7781 -0.4887 cos(ω2) sin(ω2)
0.4860 3 0.7648 0.1953 cos(ω3) sin(ω3)
0.8913 N/2=4 1.4070 0 cos(ω4) sin(ω4)=0
0.7621 5 0.7648 -0.1953 cos(ω3) -sin(ω3)
0.4565 6 0.7781 0.4887 cos(ω2) -sin(ω2)
0.0185 7 -0.6472 0.1055 cos(ω1) -sin(ω1)
Wat opvalt is dat de onderste helft van twee kolommen van X,
afgezien van het minteken voor de imaginaire bijdragen, identiek
is aan de eerste helft (d.w.z. k=0,...,N/2-1). Het
tweede deel is in feite de complex geconjugeerde (vandaar het
minteken bij het imaginaire deel) in omgekeerde volgorde van het
eerste deel.
a+ib uit twee delen
bestaat, bestaat een N-dimensionale reeks complexe getallen uit
2N reële getallen waarvan de helft met
i vermenigvuldigd is. De dimensie van een complexe
reeks is dus 2 maal die van een reële reeks. Wanneer een
reële input (van N reële bijdragen a en N
"imaginaire" nullen b) via een complexe Fouriertransformatie
omgezet wordt in een N complexe getallen
a+ib, dan is het niet zo dat de dimensie 2 keer zo
hoog wordt. Dat zou betekenen dat de zelfde reeks twee dimensies
heeft. De dimensie heeft immers te maken met het minimale aantal
(onafhankelijke) getallen die je nodig hebt om een ruimte (van
mogelijkheden) te beschrijven en dat is onafhankelijk van de wijze
waarop je die getallen combineert tot basisvectoren. Om er toch
voor de zorgen dat de "dimensionaliteit" gelijk blijft wordt
bestaat de complexe Fouriertransformatie uit N
verschillende waarden die, afgezien van k=0 en
k = N/2, elk precies 1 keer herhaald worden. Dat
gebeurt op bovenstaande wijze.
Tot slot, ter controle: de k = 0 bijdrage
(basisvector [1 1 1 ... 1]) is gelijk aan
sum(x) en de k = N/2 bijdrage
(basisvector [1 -1 1 -1 ... 1 -1]) is gelijk aan de
som van de even indexen minus de som van de oneven indexen.
sum(x) = 4.4025 % Gelijk aan cos(ω0)
sum(x([1 3 5 7])) - sum(x([2 4 6 8])) = 1.4070 % Gelijk aan cos(ω4) = cos(ωN/2)
exp(iωk) = cos(ωk) + isin(ωk),
waarbij k = 0:N-1, hiervan k = 0:N/2
uniekN/2 perioden in
een signaal van N waarden.k = 0 en k = N/2
(ofwel n = 1 en n = N/2+1) geldt dat de
imaginaire (sinus) bijdrage altijd 0 is.k = N/2+1:N, zijn FT-waarden
gelijk zijn aan de complex geconjugeerde k =
N/2-1:-1:2, ofwel vectorposities n >= N/2 in
het frequentiedomein komen overeen met golfgetal k =
N-n+1.
Een spectrum is een representatie die aangeeft wat de
energiebijdrage per k is. Energie is een kwadratische
maat, dat wil zeggen dat de energie berekend wordt door een
kwadratering van de input. Energie is, afgezien van een
willekeurig te kiezen nulpunt, altijd positief. In het tijddomein
kan de energie berekend worden door de uitwijking te kwadrateren
en alle waarden bij elkaar op te tellen. Dus:
energie_tijd = sum(x.^2) = x(1)*x(1) + x(2)*x(2) + ... + x(n)x(n)
In het frequentiedomein ziet de formule voor de energie er analoog
uit (let op de complexe conjugatie en de factor 1/N):
energie_freq = sum(X.*conj(X))/N = (X(1)*X(1) + X(2)*X(2) + ... + X(n)X(n))/N
In Matlab kan dit gecontroleerd worden met:
nfft = 8;
x = rand(1,nfft);
X = fft(x);
sum(x.^2)
sum(X.*conj(X)) / nfft % moet gelijk zijn aan sum(x.^2)
Een deel van X is redundant, alleen de bijdragen
k = 0:N/2 zijn van belang om de relatieve bijdragen
van de verschillende frequentiebijdragen weer te geven. Voor deze
k's geldt dat hun bijdrage aan het spectrum
S:
S(k) = 1/N * X(k).*conj(X(k)) k = 0 en N/2
S(k) = 2/N * X(k).*conj(X(k)) k = 1:N/2-1
In de praktijk wordt het spectrum S in Matlab
berekend als (let op n = k+1):
S = X(1:N/2+1) .* conj(X(1:N/2+1)) % Stemt overeen met k = 0:N/2
Stel dat we de eerste 4096 = 2.^12 punten (het woord "nul" van het tijddomein signaal nul123.wav grafisch weergeven.
[x, fs] = wavread('nul123.wav');
plot(x(1:4096)); axis tight
grid on;
title('Golfvorm van "nul"')
Dit ziet er zo uit:
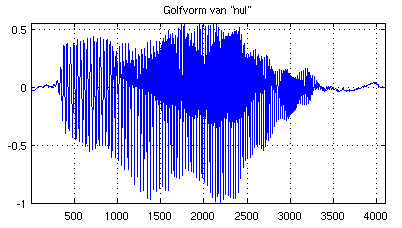
Van het hele signaal kunnen we het spectrum berekenen en zowel lineair (boven) als op een decibelschaal weergeven (onder).
nfft = 4096; % de dimensionaliteit N
X = fft(x, nfft); % FFT op basis van nfft-dim input
S = X(1:nfft/2+1) .* conj(X(1:nfft/2+1)); % Berekening energie spectrum
SdB = 10*log10(S); % omzetting naar dB-schaal
subplot(2,1,1);
plot(S); grid on; axis tight
title('Energie spectrum (lineair)')
subplot(2,1,2);
plot(SdB); grid on;
axis([1 nfft/2 max(SdB)-60 max(SdB)]) % Reductie dynamisch bereik tot 60dB onder top
title('Energie spectrum (decibel, 60 dB dynamisch bereik)')
xlabel('Basisvector nummer')
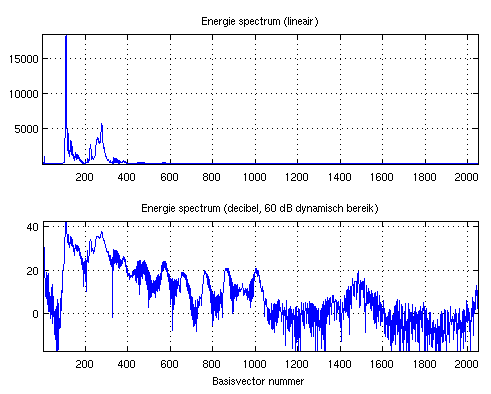
Een lineair weergegeven spectrum wordt niet vaak gebruikt want het
dynamisch bereik dat in een figuur weergegeven kan worden is dan
niet zo groot (zeg een factor 100). In de onderste figuur is het
spectrum in decibel weergegeven. Hier is het verschil tussen de
kleinste en de grootste bijdrage 60 dB, ofwel 10^6.
Voor de omrekening van en naar de dB-schaal geldt:
S_in_dB = 10 * log10(S);
S = 10 .^ (S_in_dB/10);
Tot nu toe hebben we naar frequenties verwezen via het golfgetal
k (dat het aantal gehele perioden in de basisvectoren
weergeeft). Wanneer het van oorsprongcontinue signaal gesampled
(bemonsterd) wordt met sample frequentie fs = 8000 Hz
wordt er om de 1/fs = 1/8000 = 0.000125 sec = 0.125
ms een sample gegenereerd. De tijdstap dt
tussen opvolgende samples, de duur van de signaalvector Twindow
(duur van het tijdvenster) en een vector met corresponderende
tijdstappen voor alle tijdstippen in de signaalvector worden
gegeven door:
dt = 1/fs; % tijdstap tussen opvolgende samples
Twindow = dt*N; % duur van de input in ms of s
T = dt:dt:Twindow; % vector met voor elke inputvector index een tijdstip
Voor de frequentie as geldt iets dergelijks. De laagste frequentie
(anders dan frequentie 0) die weergegeven kan worden komt overeen
met 1 oscilatie in Tmax seconden:
f1 = 1/Twindow = 1/(dt*N) = fs/N
De volgende frequenties komen overeen met k = 2, 3, 4,
etc. gehele perioden, ofwel:
fk = k*fs/N = k*df
df = fs/N % frequentieafstand tussen basisvectoren (Hz)
De volledige verzameling basisvectoren komt dus overeen met:
F = 0:df:(N-1)*df;
De hoogste frequentie die nog goed weergegeven kan worden
oscilleert N/2 keer. Met andere woorden, de hoogste
frequentie die weergeven kan worden, en die vaak de Nyquist
frequentie genoemd wordt, is
F_Nyquist = fs/2; % Nyquist frequentie
F = 0:df:F_Nyquist; % vector met bijgehorende frequentie (Hz)
voor unieke basisvectoren
Het is nu mogelijk om een tijd- of frequentiedomeinsignaal van tijd- en frequentieassen te voorzien:
nfft = 4096; % de dimensionaliteit N
[x, fs] = wavread('nul123.wav'); % inlezen datavector x
dt = 1/fs; % tijdstap tussen opvolgende samples
Twindow = dt*nfft; % duur van de input in ms of s
T = dt:dt:Twindow; % vector met voor elke inputvector index een tijdstip
subplot(2,1,1)
plot(T, x(1:nfft)); axis tight % zet x uit tegen T
xlabel('Tijd in sec')
grid on;
title('Golfvorm van "nul"')
X = fft(x, nfft); % FFT op basis van nfft-dim input
S = X(1:nfft/2+1) .* conj(X(1:nfft/2+1)); % Berekening energie spectrum
SdB = 10*log10(S); % omzetting naar dB-schaal
df = fs/nfft;
f_Nyquist = fs/2;
F = 0:df:f_Nyquist;
subplot(2,1,2);
plot(F, SdB); grid on; axis tight
title('Energie spectrum (dB)')
xlabel('Frequentie in Hz')
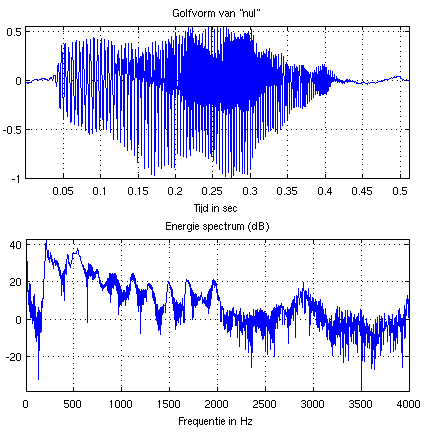
De Nyquist-frequentie is een belangrijk begrip. Als je weet
dat een signaal (zoals spraak) grotendeels onder een bepaalde
frequentie ligt kun je die frequentie als Nyquist frequentie
kiezen. Een signaal dat gesampled is met twee maal de Nyquist
frequentie kan het hele frequentiebereik onder de Nyquist
frequentie correct beschrijven. Wanneer er in het oorspronkelijke
continue signaal echter hogere frequenties voorkomen dan de
Nyquist-frequentie zullen deze signalen minder dan 2 keer per
periode bemonsterd worden. Hierdoor ontstaat een "spooksignaal"
met een frequentie die wel tussen 0 en f_Nyquist
ligt. Dit verschijnsel heet aliasing en is te voorkomen
door het continue signaal eerst zodanig te filteren dat de
frequentiebijdragen boven f_Nyquist verwijderd
worden.
postadres
Auditory Cognition Group
Kunstmatige Intelligentie
Rijksuniversiteit Groningen
Postbus 407
9700 AK Groningen
bezoekadres
Bernoulliborg
Nijenborgh 9
9747 AG Groningen