As mentioned above, the subcortical auditory system converts incoming sound waves into neural spike trains which are then processed in a very sophisticated way. Among the things that we know from physiological experiments are the following. The signals are decomposed into spectral bands that are maintained throughout the system. Autocorrelation of the signals from each of the ears, as well as cross-correlation of the signals from both ears, are performed. Specific inhibition and excitation effects are extensively present.
Models of the function of the subcortical auditory system take our knowledge of its physiology into account, but are usually oriented primarily towards the modeling of psychoacoustic findings. Most models have a signal-driven, bottom-up architecture. As an output, a (running) binaural-activity pattern is rendered that displays features corresponding to psychoacoustic evidence and/or allows for the explanation of binaural performance features. Since psychoacoustics, at least in the classical sense, attempts to design listening experiments in a ``quasi-objective'' way, psychoacoustic observations are, as a rule, predominantly associated with processes in the subcortical auditory system.
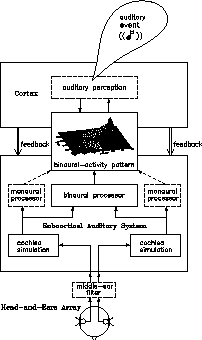
Figure A.2
: Architecture for an application oriented model of binaural
hearing: Binaural signals as delivered by the ear-and-head array (or
its electronic simulation) are fed into a model of the subcortical
auditory system, implying simulation of the function of the cochleae
and of binaural interaction as essential modules. The interface between
the subcortical auditory model and the evaluation stages on top of it
is provided by a running binaural-activity pattern.
There seems to be the following consensus among model builders. A model of
the subcortical auditory system must at least incorporate three functional
blocks to simulate binaural performance in the areas as listed above
(figure A.2
The second block includes two essential modules, cochlea simulation and simulation of subcortical binaural interaction. They will now be discussed in this order. The cochlea model simulates two primary functions, namely, a running spectral analysis of the incoming signals, and a transformation of the (continuous) mechanical vibrations of the basilar membrane into a (discrete) nerve-firing pattern: physiological analog-to-digital conversion. In doing so, it has to be considered that both spectral selectivity and A/D conversion depend on the signal amplitude, i.e., behave nonlinearly. The simplest approximation for the spectral selectivity to be simulated is by means of a bank of adjacent band-pass filters, each, for example, of critical bandwidth. This realization is often used when computing speed is more relevant than precision. More detailed modeling is achieved by including the spectrally-selective excitation at each point of the basilar membrane. The amplitude dependence of excitation and selectivity can optionally be included into the model by simulating active processes, which are supposed to be part of the functioning of the inner ear.
A more precise simulation of the physiological A/D conversion requires a stochastic receptor-neuron model to convert movement of the basilar membrane into neural-spike series. Such models have indeed been implemented for simulations of some delicate binaural effects. However, for practical applications, it is often not feasible to process individual neural impulses. Instead, one can generate deterministic signals that represent the time function of the firing probability of a bundle of nerve fibers. For further simplification, a linear dependence of the firing probability on the receptor potential is often assumed. The receptor potential is sufficiently well described for many applications by the time function of the movement of the basilar membrane, half-wave rectified and fed through of first order low-pass with a 800 Hz cut-off frequency. This accounts for the fact that, among other things, in the frequency region above about 1.5 kHz, binaural interaction works on the envelopes rather than on the fine structure of the incoming signals.
With regard to the binaural processors, the following description results from work performed in the author's lab at Bochum (e.g., [190,191,113].) First, a modified, interaural running-cross-correlation function is computed, based on signals originating at corresponding points of the basilar membranes of the two cochlea simulators , i.e., points which represent the same critical frequency. The relevance of cross-correlation to binaural processing has been assumed more than once and is, moreover, physiologically evident. A Bochum modification of cross-correlation consists in the employment of a binaural contralateral inhibition algorithm. Monaural pathways are further included in the binaural processors to allow for the explanation of monaural-hearing effects.
Some details of the binaural processors are given in the following. The first stage of the processor is based on the well known coincidence-detector hypothesis. A way to illustrate this is by assuming two complementary tapped delay lines - one coming from each ear - whose taps are connected to coincidence cells which fire on receiving simultaneous excitation from both side's delay lines. It can be shown that this stage renders a family of running interaural cross-correlation functions as output. Thus we arrive at a three-dimensional pattern (interaural arrival-time difference, critical-band frequency, cross-correlation amplitude) which varies with time and can be regarded as a running binaural-activity pattern. The generation of the running cross-correlation pattern is followed by application of a mechanism of contralateral inhibition based on the following idea. Once a wavefront has entered the binaural system through the two ears, it will consequently give rise to an activity peak in the binaural pattern. Consequently, inhibition will be applied to all other possible positions of activity in each band where excitation has taken place. In each band where signals are received, the first incoming wavefront will thus gain precedence over possible activity being created by later sounds which are spectrally similar to the first incoming wavefront, such as reflections. The actual amount of inhibition is determined by specific weights which vary as a function of position and time, such as to fit psychoacoustical data. Inhibition may, for example, continue for a couple of milliseconds and then gradually die away until it is triggered again. Using this concept as well as specific algorithm of contralateral inhibition, in combination with the inclusion of monaural pathways into the processor, the processing of interaural level differences by the binaural system is properly modeled at the same time. For certain combinations of interaural arrival-time and interaural level differences, e.g. ``unnatural'' ones, the model will produce multiple peaks in the inhibited binaural activity pattern, thus predicting multiple auditory events - very much in accordance with the psychoacoustical data [114].
To deal with the problem of natural interaural level differences being much higher at high frequencies than at low ones, the binaural processors must be adapted to the external-ear transfer functions used in the model. To this end, additional inhibitory weighting is implemented on the delay lines of the coincidence networks in such a way that the binaural processors are always excited within their ``natural'' range of operation. This additional weighting is distributed along the delay lines. The complete set of binaural processors can, thus, be conceptualized as an artificial neural network, more specifically, as a particular kind of time-delay neural network. The adaptation of this network to the particular set of external-ear transfer functions used is accomplished by means of a supervised learning procedure.
The output of the binaural processor, a running binaural-activity pattern, is assumed to be interfacing to higher nervous centers for evaluation. The evaluation procedures must be defined with respect to the actual, specific task required. Within the scope of our current modeling, the evaluation process is thought of in terms of pattern recognition. This concept can be applied when the desired output of the model system is a set of sound-field parameters, such as the number and the positions of the sound source, the amount of auditory spaciousness, reverberance, coloration etc. Also, if the desired output of the model system is processed signals, such as a monophonic signal which has been improved with respect to its S/N ratio, the final evaluative stage may produce a set of parameters for controlling further signal processing.
Pattern-recognition procedures have so far been projected for various tasks in the field of sound localization and spatial hearing, such as lateralization, multiple image phenomena, summing localization, auditory spaciousness, binaural signal enhancement, and parts of the precedence effect (see [29] for cognitive components of the precedence effect). Further, effects such as binaural pitch, dereverberation and/or decoloration are within the scope of the model.
We shall now consider the question of whether the physiological and psychoacoustic knowledge of the subcortical auditory system, as manifested in models of the kind described above, can be applied for Binaural Technology. Since we think of the subcortical auditory system as a specific front-end to the cortex that extracts and enhances certain attributes from the acoustic waves for further evaluation, signal-processing algorithms as observed in the subcortical auditory system may certainly be applied in technical systems to simulate performance features of binaural hearing. Progress in signal-processor technology makes it feasible to implement some of them on microprocessor hardware for real-time operation. Consequently, a number of interesting technical applications have come into reach of today's technology. A first category is concerned with spatial hearing, as described below.
Esprit Project 8579/MIAMI (Schomaker et al., '95)