Game Theory and the Traveler's Dilemma
The traveler's dilemma was originally created as an example of a conflict between intuition and game-theoretic reasoning. In this chapter we will explore what game theory can be used to analyze the game, what basic assumptions it makes about the players' behaviour, and how this relates to actual human behaviour.
In this chapter we will use ![]() to denote the payoff for player one (using strategy
to denote the payoff for player one (using strategy ![]() ) playing against
player two (using strategy
) playing against
player two (using strategy ![]() ).
For the traveler's dilemma, this function is:
).
For the traveler's dilemma, this function is:
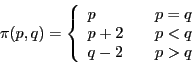
Nash Equilibria
One very important tool in game theory is a so-called Nash equilibrium [3], it defines a kind of optimal strategy. It is informally defined as a set of strategies (one for each player), such that no player can do better by choosing another strategy while keeping the others' strategies fixed. That is, if all choices of all players are known to everyone, no one would want to be the only one to switch strategies. In a two player game, it would be a pair of strategies
A strict Nash equilibrium is a set of strategies such that any player will do strictly worse by switching,
so in a two-player game it would be a pair of strategies ![]() such that
such that
![]() , etc.
, etc.
This situation is not always (in fact, usually isn't) the optimal outcome for everyone.
For example, in the prisoner's dilemma, the (strict) Nash equilibrium would be both players defecting, but the optimal outcome is both players cooperating. However, cooperation is not a Nash equilibrium because unilaterally defecting is a locally better strategy.
Likewise, in the traveler's dilemma a Nash equilibrium is ![]() . No player can do better by choosing a higher value, because they would be picking the higher value, and receive $0 as a result of the other player's choice of
. No player can do better by choosing a higher value, because they would be picking the higher value, and receive $0 as a result of the other player's choice of ![]() . This is also the only Nash equilibrium in the game, because with any other pair of strategies
. This is also the only Nash equilibrium in the game, because with any other pair of strategies
![]() , at least one player can improve their strategy by picking a value that is exactly one lower than the other player.
, at least one player can improve their strategy by picking a value that is exactly one lower than the other player.
Rationalizable Nash Equilibria
There is also the concept of a rationalizable Nash equilibrium. This involves repeated elimination of dominated strategies. A (weakly) dominated strategy is a strategy
Also note that in one experiment with game theory experts [9], one fifth of all players played the strategy $100, which is strictly dominated even without eliminating any strategies, so maybe even this very basic assumption of rationiality is too big of an assumption even without the iterative elimination of strategies.
In the traveler's dilemma, ![]() is also the only rationalizable Nash equilibrium, because, as we can see in te following table, the choice of $100 is strictly dominated by $99:
is also the only rationalizable Nash equilibrium, because, as we can see in te following table, the choice of $100 is strictly dominated by $99:
| 100 | 100 | 101 |
| 99 | 97 | 99 |
Finding this rationalizable Nash equilibrium also clearly shows the reasoning and assumptions necessary for a player to get to the conclusion that playing $2 is the 'best' strategy.
- I am a rational player, so I will not play the dominated strategy $100.
- You know I am a rational player, so you will not play the dominated strategy $99.
- I know you know I am a rational player, so I will not play the dominated strategy $98.
- You know I know you know I am a rational player, so you will not play the dominated strategy $97.
- and so on until...
- (I know you know)
 I am a rational player, so I will not play the dominated strategy $4.
I am a rational player, so I will not play the dominated strategy $4.
- You know (I know you know)
 I am a rational player, so you will not play the dominated strategy $3.
I am a rational player, so you will not play the dominated strategy $3.
- I know this, therefore I will play $2.
The assumption is also clear, it has to be common knowledge that a player will not play a dominated strategy.
This seems like a very reasonable assumption at first, but when looking at the above steps it is clear that
hardly anyone would reason that many levels deep. Indeed, it is practically impossible to imagine
the difference between ''you know (I know you know) ![]() '' and ''you don't know (I know you know)
'' and ''you don't know (I know you know) ![]() '', let alone repeating this for another
'', let alone repeating this for another ![]() steps.
steps.
Kripke models
If we would try to model the situation in a Kripke model, we would need a lot of worlds. Because both players initially have no real knowledge about what choice the other player will make, they should consider every legal number (every number from 2 to 100 in our case) as a possible choice of the other player. This has as a consequence that the needed amount of worlds to model the situation would be the square of the number of legal choices (99 in our case, with which we would get a total number of 9801 worlds). A Kripke model with this much worlds would not serve much of a purpose. To reduce the amount of worlds in the Kripke model, we greatly reduced the number of legal number choices: every player can now only choose between the numbers 2, 3 and 4. This gives the Kripke model shown in Figure 2.1.
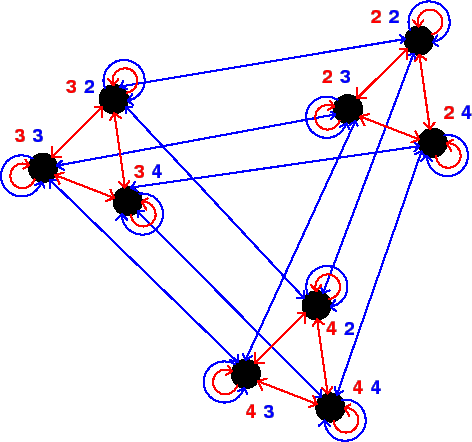 |
In this figure we can see that both players have in each world arrows to all worlds where the choice of the player itself is the same, but where the choice of the other player is different. This is because a player obviously knows which number it chooses, but does not know which number the other player chooses.
If, in this situation, it would become common knowledge that choosing 4 is not rational because it means playing the dominated strategy $4, and it is common knowledge that both players are rational, then the Kripke model can be reduced to the Kripke model shown in Figure 2.2.
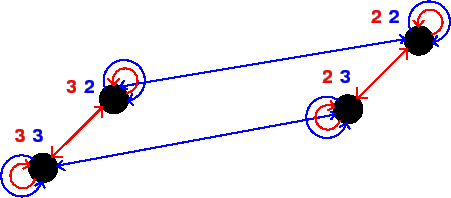 |
As can be seen by comparing this model to the previous one, this model is the previous model but without the worlds where one of the players would choose 4.
Similar to removing all world with choice 4, all worlds with choice 3 can also be removed, as playing $3 has now become a dominated strategy. This gives the Kripke model shown in Figure 2.3.
 |
In this Kripke model, it is common knowledge that both players will play $2. This is caused by the assumption that both players are rational and won't play dominated strategies, as described before. So in fact there is only one possible world for both players, because they know both their choice and the choice of the other player.
Another way to model the dilemma could have been to just have one world where both players are rational and both players have reflexive arrows, so it is common knowledge that they are rational. This would not be an interesting Kripke model, but the model would be able to graphically support the ''I know that you know that I know ...''-reasoning as described before.
Either way, it does not seem to be very useful to model the (entire) situation in a Kripke model. You would either have an enormous amount of worlds, or you could reason to the point that both players will play $2 and have only one world. Both cases do not seem to give more insight into the situation.
A bigger reward?
Increasing the honesty reward
However, it is easier to be rewarded for an uncooperative strategy. When the reward is two, choosing a value more than two below the other player's choice is worse than choosing the same strategy as him, and being more than three below it even means the 'completely irrational' choice of $100 would have been better.
Capra et al. [10] also looked at increasing the reward. They show that, as the reward increases, the players are more and more intended to go to the Nash equilibrium. For the low reward fees (from $1), the average claim is close to the maximum claim. But as the reward increases, the players are willing to take a bit more risk for a higher payoff. And finally, for the largest values of the reward (with a maximum of $40), the average reaches the Nash equilibrium.
They conclude that, however the game should not be influenced by the reward, according to the Nash equilibrium, in fact it is when tested in real life. This does not mean that the Nash equilibrium is a wrong method, only that it fails to explain human behaviour for this problem.
Evolutionary stable strategies
Closely related to the theory of Nash equilibria is the concept of an evolutionary stable strategy [3]. A strategy
Whereas in a Nash equilibrium no player can benefit from switching,
in a non-strict equilibrium a different strategy that has an identical payoff is still allowed.
This is justified by the assumption that a player has no incentive to switch from the equilibrium, because it would not benefit him.
However, in an evolving population there does not need to be an incentive (i.e. a fitness advantage) to switch, because
genetic drift is sufficient to cause divergence from the equilibrium in the absence of a penalty for doing so.
Therefore, a stricter concept is needed, one of these is the evolutionary stable strategy.
Originally developed by John Maynard Smith [4] for use in theoretical biology , it has also been used in game theory, economics and many other fields of research.
It is defined as a strategy ![]() for which for all other strategies
for which for all other strategies ![]() the following conditions hold:
the following conditions hold:
-
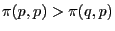 or
or
-
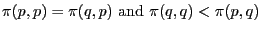
The first condition is the same as for the strict Nash equilibrium, so all strict Nash equilibria are evolutionary stable strategies.
Maynard Smith's second condition signifies that even though the strategy ![]() is neutral when playing against
is neutral when playing against ![]() , the population
of players who continue to play strategy
, the population
of players who continue to play strategy ![]() still have an advantage over those playing strategy
still have an advantage over those playing strategy ![]() , when meeting a
, when meeting a ![]() -strategist.
-strategist.
This definition shows that every ESS is also a (possibly non-strict) Nash equilibrium, but not every non-strict Nash equilibria is an ESS. Consider a game with the following payoff matrix:
| C | D | |
| C | (1,1) | (0,0) |
| D | (0,0) | (0,0) |
| C | D | |
| C | (1,1) | (1,1) |
| D | (1,1) | (0,0) |
For the traveler's dilemma, ![]() is also an ESS, simply because it is a strict Nash equilibrium.
is also an ESS, simply because it is a strict Nash equilibrium.
Sometimes a stronger definition is used, proposed by Thomas [5], which stresses the importance of the payoff of invaders more: :
-
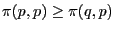 and
and
-
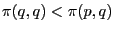
In this case, not all strict Nash equilibria are ESS. Also, any ESS according to this definition is also
an ESS according to Maynard Smith's definition.
For the traveler's dilemma, ![]() is an evolutionary stable strategy according to the first definition but not according to the second, after all
is an evolutionary stable strategy according to the first definition but not according to the second, after all
![]() .
.
Simulation
Because we can not simulate human players, we will try to simulate a population of 'travelers' evolving, and see if the Nash equilibrium appears as a result.Methods
We simulated a population of travelers using a co-evolutionary genetic algorithm [6]. A co-evolutionary GA does not use a fitness function to rate the various solutions, but rates their performance when several members of the population 'fight' eachother in some way.
We used the genetic algorithms library 'charlie' [7], for the Ruby programming language. Source code can be seen in the appendix.
For the selection algorithm, we used the built-in CoTournamentSelection.
In this algorithm, groups (tournaments) of size ![]() were created, and all travelers play a single-shot traveler's dilemma against all others in the group. After all these games have been played, the group was replaced by a normal round of roulette selection, taking their total score over all these games as their fitness values.
This means the fitness of an individual is its average performance in playing single-shot traveler's dilemma games when facing other individuals in the tournament group.
In each generation, enough of these tournaments are played such that roughly the entire population is replaced once, so the generations listed here are technically 'generation equivalents'.
were created, and all travelers play a single-shot traveler's dilemma against all others in the group. After all these games have been played, the group was replaced by a normal round of roulette selection, taking their total score over all these games as their fitness values.
This means the fitness of an individual is its average performance in playing single-shot traveler's dilemma games when facing other individuals in the tournament group.
In each generation, enough of these tournaments are played such that roughly the entire population is replaced once, so the generations listed here are technically 'generation equivalents'.
No crossover was used, since the genotype is only a single number.
Mutation rate was set at ![]() , that is, half of the children are different from both their parents, and the other half are identical to one of their parents. Mutations were applied by adding a Gaussian distributed random number (
, that is, half of the children are different from both their parents, and the other half are identical to one of their parents. Mutations were applied by adding a Gaussian distributed random number (![]() ) to the gene, and then clamping it to the range
) to the gene, and then clamping it to the range
![]() .
The population size was set at the default 20 with random initialization, and the algorithm was run for 1000 generations.
.
The population size was set at the default 20 with random initialization, and the algorithm was run for 1000 generations.
The honesty reward was varied between ![]() and
and ![]() , and for each different reward the GA was run for a variety of mutation
and tournament sizes.
For the tournament sizes we used the full possible range
, and for each different reward the GA was run for a variety of mutation
and tournament sizes.
For the tournament sizes we used the full possible range
![]() , and
for the mutation sizes we used
, and
for the mutation sizes we used
![]() , so in total
, so in total ![]() runs were done for each different reward.
runs were done for each different reward.
We repeated all these tests using a population which was initialized at the minimum value possible, which is the honesty reward. This way we could study the non-ESS results in the other tests to see where they were caused by a failure to converge within the limited number of generations, and where the population actually escaped from the ESS.
Results
Because of the vast amount of results (about 40 million generations) we can not present, or even examine, all the data.
Instead we only look at the average move in the population at the end of a run,
and visualized these results using MATLAB.
The images can be interpreted as follows: On the horizontal axis is the mutation size ![]() , increasing from left to right and
on the vertical axis is the tournament size
, increasing from left to right and
on the vertical axis is the tournament size ![]() , increasing from top to bottom.
Each single rectangle, of which there are
, increasing from top to bottom.
Each single rectangle, of which there are
![]() in each image, represents the average strategy in the population after 1000 generations and is represented by a color which
can be looked up in the bar to the right of the image. In general bright red represents a value close to the maximum
in each image, represents the average strategy in the population after 1000 generations and is represented by a color which
can be looked up in the bar to the right of the image. In general bright red represents a value close to the maximum ![]() , and
blue a value close to the minimum value.
, and
blue a value close to the minimum value.
![\includegraphics[width=6cm]{out3.eps}](img69.gif) |
|
![\includegraphics[width=6cm]{out4.eps}](img70.gif) |
![\includegraphics[width=6cm]{out5.eps}](img71.gif) |
![\includegraphics[width=6cm]{out6.eps}](img72.gif) |
![\includegraphics[width=6cm]{out7.eps}](img73.gif) |
![\includegraphics[width=6cm]{out8.eps}](img86.gif) |
![\includegraphics[width=6cm]{out9.eps}](img87.gif) |
![\includegraphics[width=6cm]{out10.eps}](img88.gif) |
|
Table 2.4 shows the results for the experiments with random initialization.
When using a tournament size of ![]() the population converges to the minimum value for all settings.
This can be easily explained by the fact that the fitness value in this case is just
the population converges to the minimum value for all settings.
This can be easily explained by the fact that the fitness value in this case is just ![]() ,
i.e. those individuals who simply have a higher payout than their opponent, regardless of what this payout is, are more successful.
For bigger tournaments, an individual can 'win' every game and still have the lowest average, for example a $2 player in a population of $100 players.
These results then do not really represent what we want to model, which is maximizing your payout itself and not your payout relative to a single opponent. However, they can still be used as a baseline for the amount of convergence and amount of drift when there is a clear selective pressure for the lower strategies. Likewise, the bottom row, for a tournament with the entire population, is closest to the actual traveler's dilemma and therefore contains the most important results.
,
i.e. those individuals who simply have a higher payout than their opponent, regardless of what this payout is, are more successful.
For bigger tournaments, an individual can 'win' every game and still have the lowest average, for example a $2 player in a population of $100 players.
These results then do not really represent what we want to model, which is maximizing your payout itself and not your payout relative to a single opponent. However, they can still be used as a baseline for the amount of convergence and amount of drift when there is a clear selective pressure for the lower strategies. Likewise, the bottom row, for a tournament with the entire population, is closest to the actual traveler's dilemma and therefore contains the most important results.
Looking at figure 2.4(a), it is clear that most runs other than the ![]() results converge to a high value, somewhere in the range $85 - $100.
For higher rewards, a front appears from which on one side (small tournament size and especially, low mutation) the results converge to the minimum value, and on the other side converge to a value near the maximum.
results converge to a high value, somewhere in the range $85 - $100.
For higher rewards, a front appears from which on one side (small tournament size and especially, low mutation) the results converge to the minimum value, and on the other side converge to a value near the maximum.
For larger reward, there are no longer any settings that don't converge to the minimum, although figure 2.6 shows this is just an effect of the maximum mutation size.
These experiments were repeated starting with populations with every individual at the minimum value, so right in the ESS.
Maynard Smith's definition of an ESS suggests that it should be very unlikely for the population to escape the ESS,
but as can be seen in table
2.5, the results are very similar.
Only the parts which had somewhat inconclusive results in the previous experiments now clearly stay at the ESS, but this did not because the boundaries shift much, instead they just become sharper.
For example, in the ![]() figures in the bottom
figures in the bottom ![]() rows, the boundary to the right of which all results are
rows, the boundary to the right of which all results are ![]() is at about
is at about ![]() , whereas in the ESS results it is at about
, whereas in the ESS results it is at about ![]() .
.
Clearly, the second definition of an evolutionary stable strategy is the better one here, and also explains
why the first definition fails.
Simple calculations show that when there is sufficient variation in the population, the strategy with the highest payoff is in fact above the average of the other strategies. This explains the selective pressure towards higher strategies, and with it possibly the strategies seen in real life.
Conclusion
Classic game theory fails to explain human behaviour when playing the traveler's dilemma, but can still be used to see what assumptions are being made. Common knowledge of rationality rarely exists, because most people are just not inclined to think more than a few levels deep. Even game theory experts don't assume this when playing against each other.Instead of talking about rational or irrational choices, it may be better to see the game as one with various levels of cooperation. We think most people would expect others to be cooperative (i.e. conspire against the insurance company), and would therefore pick a high value. Unlike some other games, even uncooperative players who know for sure their opponent is cooperative are best off picking a value above the average strategy of their opponents if they can not estimate these strategies to within a very narrow range. This basically forces them to be cooperative as the only optimal strategy.
Only when the reward for being uncooperative is high enough, and the variation in your opponents' strategies is small enough, is it possible to play an optimal strategy at the expense of all others, and will the strategies likely trend towards the Nash equilibrium.
![\includegraphics[width=6cm]{out2.eps}](img68.gif)
![\includegraphics[width=6cm]{st2out2.eps}](img77.gif)
![\includegraphics[width=6cm]{st2out3.eps}](img78.gif)
![\includegraphics[width=6cm]{st2out4.eps}](img79.gif)
![\includegraphics[width=6cm]{st2out5.eps}](img80.gif)
![\includegraphics[width=6cm]{st2out6.eps}](img81.gif)
![\includegraphics[width=6cm]{st2out7.eps}](img82.gif)
![\includegraphics[width=6cm]{st2out8.eps}](img89.gif)
![\includegraphics[width=6cm]{st2out9.eps}](img90.gif)
![\includegraphics[width=6cm]{st2out10.eps}](img91.gif)
![\includegraphics[width=11cm]{outlarge15.eps}](img93.gif)