informatie   rooster   hoorcollege   practicum   links

Robuuste spraakdetectie

Bij dit practicum mag je zoveel samenwerken en overleggen als je wilt, zolang ieder maar een volledig eigen tekst inlevert (eventuele plaatjes mogen worden gecombineerd). De opdrachten van dit practicum staan geheel in dienst van het deeltentamen. Ze moeten je helpen om de problematiek van spraakdetectie zo goed mogelijk te demonstreren.

onderwerpen

• optelling van geluiden
• signaal-ruisverhouding (SNR)
• spontane spraak in ruis
• onbekende (spraak)signalen in ruis

Optelling van geluiden

Wanneer geluidsbronnen mengen (wat natuurlijk in normale transmissieomstandigheden altijd gebeurt) kan dat in zeer goede benadering gezien worden als een optelling van het geluid van de aanwezige bronnen. Helaas geldt dit niet voor de energiespectra van het signaal. Een extreem geval zijn de signalen x(t) en -x(t). Wanneer deze opgeteld worden blijft er niets (dus ook geen energie) over.

Wanneer twee signaalbijdragen van vergelijkbare frequenties opgeteld worden zal er zweving optreden: zo nu en dan versterken de signalen elkaar en zo nu en dan verzwakken ze elkaar. De effecten hiervan zijn in een cochleogram altijd lokaal, maar het effect kan groot zijn, zeker wanneer beide signalen ongeveer gelijke amplitudes hebben. In het volgende script worden twee geluidssignalen gemaakt. Een zuivere sinus met de frequentie van segment 100 (883 Hz bij een hoogste frequentie van 6000 Hz en 200 segmenten) (bovenste subplot) en smalbandige ruis met frequenties die horen tussen segment 101 en 99 (865 en 902 Hz). (Onderstaande niet uitvoeren, alleen ter illustratie!)
N.B. De frequenties gegeven bij de segmentnummers gelden voor deze instellingen. Wanneer je het aantal segmenten of de maximale frequentie aanpast zullen deze relaties niet meer hetzelfde zijn.

    fs = 8000;
    duration = .1;
    %fftSize = fs * duration;
    t = linspace(0, duration, fs/10);
    figure
    % maakt zuivere sinus, van duration sec.
    [x, info, X] = makeGausSignal(fs, 0, env.fm(100), 1, 0, duration);
    % delen door root-mean-square van x (gemiddelde energie)
    x = x ./ sqrt(mean(x.^2));
    % maakt "energie per tijdstap" van x gemiddeld 1.
    subplot(3,1,1); plot(t, x); axis([0 duration -3 3])
    title('Pure sine for segment 100')
    % maakt ruis ter breedte van de frequenties horend bij segment 100.
    [xn, info, X] = makeGaussSignalWeber(fs, .5, env.fm(100), inf, ...
                    ... (env.fm(99) - env.fm(101)) / env.fm(100), duration);
    xn = xn ./ sqrt(mean(xn.^2));
    subplot(3,1,3); plot(t, xn); axis([0 duration -3 3])
    title('Narrow band noise for segment 100')
    xlabel('Time in sec');
    subplot(3,1,2); plot(t, x + xn); axis([0 duration -3 3])
    title('Sum of pure sine and narrow band noise');
    

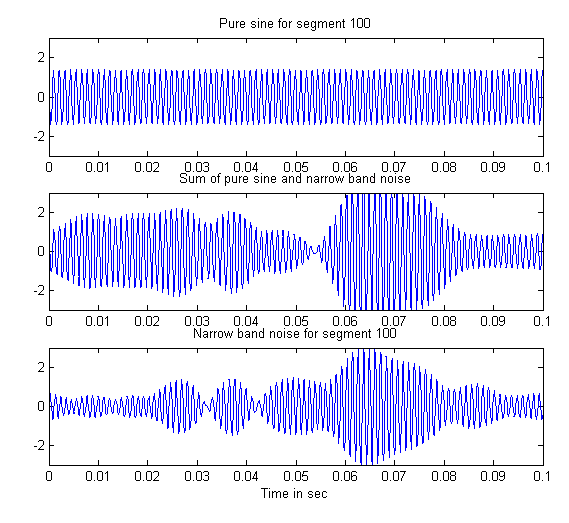
De sterk variërende temporele omhullende in de onderste subplot is het gevolg van de zweving tussen de verschillende componenten van de ruis. De tweede subplot laat de optelling zien tussen het ruissignaal en de zuivere sinus.

opdracht A

1. Geef een tijdstip aan in de middelste grafiek waarin er sprake is van destructieve interferentie tussen het bovenste en het onderste signaal. En wanneer is er constructieve interferentie?
2. Beredeneer waarom zweving niet of minder van belang is voor a) signaalcomponenten met grote frequentieverschillen en b) voor signaalcomponenten met grote (bijv. groter dan 6dB) intensiteitsverschillen.

Signaal-ruisverhouding (SNR)

Door het werk van Bell-lab onderzoeker Fletcher is het al meer dan 50 jaar bekend (French 1947, Allen 1994) dat de lokale signaal-ruis verhouding (signal-to-noise-ratio, SNR) op het basilair membraan (BM) bepalend is voor het verstaan van spraak. Hierbij verwijst het woord "lokaal" naar de omgeving van een punt in tijd en plaats (frequentie) in het cochleogram / spectrogram. Dit geldt niet alleen voor het verstaan van spraak, de lokale SNR is voor alle vormen van geluidherkenning bepalend. In het algemeen kan worden gezegd dat een positieve SNR nodig is (d.w.z. een dB-waarde > 0, ofwel dat het signaal lokaal sterker is dan dan de "ruis") voor herkenning. Volgens Fletcher neemt het belang van een omgeving in het f,t-vlak ongeveer lineair toe bij SNR-waarden tussen 0 dB en 30 dB. Onder de 0 dB kan er geen zinvolle informatie aan een gebied ontleend worden en boven de 30 dB is het voor dat gebied net alsof er geen ruis aanwezig is. Conclusies die hieruit te trekken zijn, zijn onder meer:

• Alleen gebieden met een positieve SNR dragen bij aan het interpreteren van een signaal.
• Wanneer een omgeving in het f,t-vlak gedomineerd wordt door een bepaalde bron kunnen we dit gebied gebruiken om de bron te herkennen.
• Geluidsbronherkenning is in eerste instantie gebaseerd op een lokale analyse (zie artikel van Allen).

Een niet onbelangrijk detail is dat Fletcher werkte met "structuur-arme" witte ruis. Dit is een soort geluid die in realistische omstandigheden relatief weinig voorkomt. Meestal is het achtergrond geluid ook sterk gestructureerd. Luister bijvoorbeeld eens naar babble-noise. Het nadeel van witte ruis voor dit soort experimenten is dat elk geluid met een structuur die afwijkt van de gemiddeld vlakke ruis direct als afwijkend van de ruis gewaarmerkt kan worden. Dit maakt het relatief gemakkelijk om potentieel interessante signalen te detecteren.

Het belang van de lokale SNR is nog zeker geen gemeengoed. In alle automatische spaakherkenningssystemen wordt ervan uitgegaan dat de spectrale vorm (de omhullende van het spectrum, zoals gecodeerd in een MFCC) de belangrijkste determinant voor herkenning is. Het blijkt echter dat wanneer de spectrale vorm veranderd wordt (door filters, ruis of door het signaal eenvoudigweg op te nemen in een normale akoestische omgeving), het spectrum ernstig verstoord kan worden zonder dat de verstaanbaarheid of zelfs de klankkleur aangetast wordt. De prestaties van automatische spraakherkenners die uitgaan van een vaste en bekende spectrale vorm worden al door kleine veranderingen ernstig aangetast en zijn daardoor in de praktijk vaak onbruikbaar.

Omdat we een (spraak)geluidherkenningssysteem proberen te ontwerpen dat in alle dagelijkse situaties even goed werkt als het menselijk systeem, moeten we eens kijken wat de signaal-ruisverhouding op het BM eigenlijk betekent. Even terzijde: de ruis hoeft geen aperiodieke min of meer constante ruis te zijn. Het mag elk willekeurig signaal zijn, de enige eis aan de ruis is dat het niet hetgeen is waarin je geïnteresseerd bent. Een beter term hiervoor is target-to-nontarget-ratio. We zullen ons echter houden aan de conventie signal-to-noise-ratio (SNR).

De signaal-ruisverhouding is de verhouding tussen de energie T van het (doel)signaal en de energie N van een ander signaal dat ruis (noise) genoemd wordt. Dus: SNR=T/N. Omdat deze verhouding vaak een groot bereik kan omvatten wordt de SNR meestal in dB uitgedrukt:

    SNR = 10*log10(T/N) % in dB
    

Een SNR van 3 dB is dus een verhouding waarbij T = 2*N en voor een SNR van -20 dB geldt: T = 0.01*N.

De energie van een geluidssignaal kan berekend worden als som van het gekwadrateerde signaal. Dus de energie van geluidssignaal x1 is:

    T = sum(x1.*x1);
    

Een probleem hierbij is dat de op deze wijze berekende energie een globale maat is die voor het gehele signaal geldt, terwijl de verstaanbaarheid van het (spraak)geluid bepaald wordt door de lokale SNR, dat wil zeggen de SNR op of rond een bepaald punt in het tijd-frequentievlak E(f,t). Wat we eigenlijk willen weten om iets over de verstaanbaarheid te kunnen zeggen is een lokale SNR(f,t) ofwel:

    SNR(f,t) = 10*log10(E2(f,t) ./ E2(f,t));
    

Wanneer de energieën uitgedrukt worden in dB volgens TdB = 10*log10(T) en NdB = 10*log10(N), vereenvoudigt de berekening van de SNR tot:

    SNR(f,t) = TdB(f,t) - NdB(f,t)
    

Dit geldt zowel voor in dB uitgedrukte fft-spectra S(f,t) als voor in dB uitgedrukte cochleogrammen D.EdB(s,t). Met andere woorden, wanneer we de lokale SNR van een signaal x1 en een stoorsignaal x2 willen berekenen moeten we de corresponderende spectrogrammen van elkaar aftrekken.

Dit wordt hieronder gevisualiseerd. Kies addNoise (met onder config als Noise type Babble) en plotProcessSound in functionsTest, en bereken het cochleogram van nul123.wav nadat je de Absolute energy onder config van calcEdB hebt aangevinkt. Bewaar de resulterende D-structuur in Dxb. Bereken opnieuw het cochleogram van nul123.wav, maar nu zonder toegevoegde babble noise. Het originele signaal staat in D.audio.orig, als je deze opslaat in een aparte variabele, x = D.audio.orig, dan kan je het cochleogram berekenen via Run Var in functionsTest. (Zorg dat je de juiste sample frequentie invoert en verwijder addNoise uit de lijst!) Bewaar de resulterende D-structuur in Dx. Bereken als laatste het cochleogram van alleen de babble noise via Run Var (b = D.audio.noise) en bewaar de D-structuur in Db. Wanneer je de D-structuren van alle drie de signalen hebt, voer dan de volgende commando's uit.

maxGlob = max([max(Dx.EdB(:)) max(Db.EdB(:)) max(Dxb.EdB(:))]);
figure
subplot(2,2,1);
imagesc(Dx.EdB, maxGlob + [-60 0]); set(gca, 'xticklabel', ''); colorbar
title('Clean');
subplot(2,2,3)
imagesc(Db.EdB, maxGlob + [-60 0]); colorbar
title('Babble noise')
subplot(2,2,4)
imagesc(Dxb.EdB, maxGlob + [-60 0]); colorbar
title('Noisy signal')
subplot(2,2,2)
imagesc(max(0, Dx.EdB - Db.EdB)); set(gca, 'xticklabel', ''); colorbar
title('SNR in dB (only positive)')

opdracht B

1. Plot een cochleogram van de eerste 2 seconden van babble.wav en beschrijf een aantal (vage) spraakachtige structuren (zoals formanten en harmonischen).
2. Waarom zijn in de rechterbovenplot van het vorige figuur alleen positive dB-waarden weergegeven?
3. Geef aan waarom de subplot rechtsboven een bevestiging is van postulaat 1.2 van het proefschrift:
   "The most important (linguistic) information in a speech signal is represented by those signal properties that can be estimated by the human auditory system in the widest possible range of real-life conditions. These signal-properties are, by definition. the most robust properties."

Vaak is de globale SNR een aardige indicatie voor de verstaanbaarheid van een signaal. De globale SNR kan berekend worden door de totale energie van het doelsignaal te delen door de energie van de ruis.

10*log10(sum(x(:).^2) ./ sum(b(:).^2)) % SNR in dB, tijddomein berekening 10*log10(sum(Dx.E(:)) ./ sum(Db.E(:))) % SNR in dB, cochleogramdomein berekening

Dit geeft dit een SNR die ongeveer gelijk is aan de SNR aangegeven in de config van addNoise (default 0). Een onbekend breedbandig communicatief signaal zoals spraak wordt in breedbandige ruis (zoals babble-noise) tot ongeveer -3 dB nagenoeg foutloos herkend door normaalhorende luisteraars. Het 50% punt, waarbij de 50% van korte zinnen niet geheel goed wordt herkend, ligt rond de -6 dB. Beneden de -10 dB is de herkenning minimaal. Een bekend signaal kan echter in nog wat meer ruis worden teruggevonden.

In tegenstelling tot de code hierboven kan met addNoise het ruissignaal gewogen worden, zodat het (bij benadering) een bepaald aantal dB's sterker wordt. Na de uitvoering van addNoise wordt een tijddomein schatting van de globale SNR opgeslagen onder processSoundConf.addNoise.SNR. De cochleogramdomein berekening kan je op dezelfde manier als hierboven berekenen.

Run het cochleogram op dezelfde manier als beschreven voor opdracht B, maar selecteer nu plotNSC2, zodat de NSC's zichtbaar worden in het cochleogram. Zorg dat je cochleogram 100 segmenten heeft (onder Config Cochlea in functionsTest) en Noise bias op 0 dB staat (is de default).
N.B. Door onder Plot tools in functionsTest telkens New figure te kiezen, komen de cochleogrammen telkens in een nieuw figuur.

Laat het drietal cochleogrammen (dus van signaal+ruis, het schone signaal en de ruis) naast elkaar open, zodat je ze met elkaar kunt vergelijken. Het is verstandig de figure smal en hoog (maximale schermhoogte) te maken zodat je de afzonderlijke NSC's makkelijk kunt onderscheiden.

opdracht C

1. Zoek een NSC die deels bij de ruis hoort en deels bij het doelsignaal. Geef van deze NSC de combinatie van frame- en segmentnummer van de start en het eind en geef aan wat de functie van de ridge is voor het deel dat het van de target uit maakt.
2. Hoe kan het deel van de NSC dat van de target afkomstig is aan een representatie van de target worden gekoppeld?
3. Probeer op basis van de grafieken ongeveer te schatten welk percentage van de "target NSC's" (dus NSC's die in ieder geval gedeeltelijk de harmonischen beschrijven) voor een belangrijk deel uitmaakt van de target woorden.

We gaan de SNR nu in de buurt van de menselijke perceptiegrens brengen door de noise bias op 6 en later 9 te zetten (wat geeft dit als globale SNR?). Doe dit door onder config van addNoise de Noise bias te veranderen naar 6 dB en als Noise type weer Babble. Bereken het cochleagram en sla de D-structuur op in Dxb6. Bereken de het cochleogram van de babble noise en sla de D-structuur op in Db6. Doe hetzelfde voor een noise bias van 9 dB en controleer de afname van de SNR.
N.B. Een D-structuur van het schone signaal, Dx, heb je nog van hierboven.

opdracht D

1. Luister met behulp van Play Ruler in Plot tools naar de drie signalen met een noise bias van 0, 6 en 9 dB.
   Bij welke SNR ben je niet meer zeker dat je de (bekende) target kunt verstaan?
2. Plot de positieve lokale SNR:
   

   figure, imagesc(max(0, Dx.EdB - Db9.EdB)); set(gca, 'xticklabel', ''); colorbar
   title('SNR in dB (only positive)')

   Hoewel er nog steeds delen zijn met positieve SNR's is het signaal toch niet meer te verstaan. Geef hier een verklaring voor.

Spontane spraak in ruis

Neem een fonetisch rijke zin op. Neem een sample frequenctie van 22050 Hz. Zorg er ook voor dat de zin niet te lang is (< 15 sec) in verband met de lengte van de ruis en de verwerkingstijd. Zet in fucntionsTest de noise bias zonodig weer op 0 dB en zet de hoogste frequentie Fmax in Config Cochlea op 8 of 10 kHz zodat de stemloze delen ook goed zichtbaar zijn. Bereken vervolgens het cochleogram.

opdracht E

1. Bepaal in de fonetisch rijke zin bij welke SNR stemloze delen optisch niet meer waarneembaar zijn.
2. Ondanks het feit dat de stemloze delen bij deze SNR niet meer zichtbaar zijn kun je ze toch nog "horen". Geef hiervoor een verklaring.
3. Bepaal de SNR waarbij het signaal niet meer goed verstaanbaar is. Gebruik hiervoor:
   10*log10(sum(Dx.E(:))./sum(Db.E(:)))

Neem nu een willekeurige korte zin op (fs>12 kHz, 16 bits). Doe je best om die zo spontaan mogelijk te laten klinken. Doe in het bijzonder je best om de zin vooral niet te laten klinken alsof het voorgelezen is. Bereken het cochleogram.

opdracht F

1. Teken een rechthoek met de vorm van het tijd-frequentie assenstelsel van het cochleogram. Geef in de het assenstelsel aan waar je de linguïstisch belangrijke informatie van de zin kunt vinden. Geef formanten (ook van stemloze delen) aan met gesloten contouren, geef plofjes aan met verticale lijnen. Geef ook de toonhoogte contour aan. (Laat de harmonischen/ridges weg). Zorg ervoor dat je aannemelijk kunt maken dat er voldoende informatie is om de zin correct te herkennen.
   Als optie kun je op basis van dit plaatje een schatting maken van de hoeveelheid parameters (of zelfs bits) die je per seconde nodig hebt om een spraaksignaal te beschrijven. Dit geeft je een idee (bovengrens) van de informatieoverdrachtssnelheid in een gesprek.
2. Geef een indicatie van de gemiddelde duur (seconden) van een linguïstische eenheid (lettergreep).
3. Voeg nu zoveel ruis toe dat het signaal nog foutloos te verstaan is, maar dat het wel in de buurt van de verstaanbaarheidsgrens ligt (SNR ongeveer 0 dB). Geef in de tekening (met een andere kleur/structuur) aan welke delen nu nog een SNR hebben die > 6 dB (dit zijn wel NSC's). Deze informatie kun je vinden met bijvoorbeeld:

   SNRlocal = Dx.EdB - Db.EdB;
   figure, imagesc(SNRlocal .* (SNRlocal > 6))

Je mag aannemen dat de laatst toegevoegde informatie voldoende is om:

• het menselijk spraakanalyse systeem te attenderen op deze spraakuiting,
• de spraakuiting correct te herkennen.

Je hebt nu een figuur die aangeeft waar de linguïstische informatie in schone spraak zich bevindt en die tegelijkertijd een soort minimum informatie aangeeft die toch voldoende is om het signal correct te verwerken.

Onbekende (spraak-) signalen in ruis

Maak nu een opname van een korte zin op zodanige wijze dat je practicum partner niet weet wat er gezegd is (stuur hem/haar even weg). Voeg ruis toe tot ongeveer 0 dB en bereken het cochleogram met NSC's (met plotNSC2). Laat je partner op basis van hiervan vaststellen wat target is en wat ruis. Je partner functioneert nu als een soort aandachtssysteem.

opdracht G

1. Wat voor heuristieken gebruikt hij/zij om vast te stellen wat spraak en wat ruis is? Deze informatie vertelt je, als het goed is, hoe je met de verwerking van een ruizig signaal kunt beginnen. Wissel zo nodig van functie met je practicum partner.

Referenties

Allen, J.B. (1994), "How Do Humans Process and Recognize Speech?", IEEE Transactions on Speech and Audio Processing 2(4), pp 567-577.
French, N.R. and Steinberg, J.C. (1947), "Factors Governing the Intelligibility of Speech Sounds", Journal of the Acoustical Society of America 19(1), pp 90-119.