

voorbereiding
Lees de teksten over CPSP in de klapper van te voren door zodat je
zo ongeveer weet wat een cochleogram is en hoe de datastructuren
eruit zien. Deze tekst dient vooral als referentie. CPSP wordt in
dit practicum vooral gezien als een methodiek voor signaalanalyse
en minder als een methode om het auditief systeem te begrijpen
(hoewel het daar bij helpt). CPSP is (wellicht net als het
auditieve systeem) geoptimaliseerd om in het input signaal
informatie over de aanwezigheid en de ontwikkeling van individuele
bronnen te kunnen vaststellen. Het volgen (tracking) van
signaalcomponenten is daarom heel belangrijk. De reden waarom CPSP
voor dit doel handiger is dan op FFT-gebaseerde methoden is dat er
gebruik gemaakt wordt van de continuïteit van het basilair
membraan model. Dit is niet geval bij een FFT waar bij ervan
uitgegaan wordt dat alle informatie die je nodig hebt aanwezig is
in een window (van bijvoorbeeld 25 ms). Door de frame gebaseerde
aanpak is een FFT-spectrum vooral geschikt voor analyse per frame,
ofwel de verticale richting van een spectrum, terwijl het in CPSP
(en in het auditief systeem) ook gemakkelijk is in om temporele
(horizontale) richting te analyseren.
/home/soundrecognition/cpsp/current/. Zorg dat je
startup in matlab draait in deze directory (als je
matlab opstart in deze directory wordt startup automatisch door
matlab gedraaid).plotNSC2 en
calcRS. Zet het referentie spectrum op uniform
m.b.v. Config, en kies in Config van plotNSC2 voor Show EdB. Verwerk de file nul.wav met Run Wav. Met plotNSC2 zie je behalve het cochleogram ook signaalcomponenten (de witte lijnen). De horizontale signaalcomponenten in spraak zijn schattingen van de harmonischen.plotNSC2 of calcNSC2
berekent. Daarna wordt alle informatie opgehaald uit een
hash-file, dus zal het veel sneller gaan (als je de instellingen
niet verandert!) Wanneer je op een /tmp schijf werkt is het
daarom handig deze hash-file (in
matlab/processSoundFunctions/initPAS/cache/) te bewaren op je
eigen schijf, en bij een nieuwe installatie op dezelfde plek
terug te zetten.
Config TFProcessor en bekijk het resulterende
cochleogram (met plotProcessSound
i.p.v. plotNSC2). Door de aanpassing van het aantal
segmenten moeten een aantal zaken opnieuwe worden berekend. Dit
kan even duren. Kom zolang Matlab "busy" is niet aan de knoppen
van de interface (Matlab vindt dat niet leuk!). Het cochleogram
is nu nog wat scherper omdat de frequentieresolutie hoger is.calcRS uit de lijst en bereken weer het
cochleogram. Nu worden de hogere frequenties minder goed
zichtbaar.Config van calcEdB kan je de instellingen van het dynamisch bereik veranderen. Wanneer je bijvoorbeeld een klein dynamisch bereik hebt kan je limit EdB aanklikken. Als je vervolgens op Recalculate klikt krijg je een vernieuwde plot.
Toets env in de Matlab command window. Als het goed
is vind je voor de belangrijkste parameters:
env =
gdCorrection: 0
nseg: 100
maxf: 4000
desiredFrameSize: 5
Qfac: 0.0500
tau: 0
nPeriod: 2
energyCorFac: 1.0000e+10
maxDiff: 0.0050
initdep: 1
amplitudeMatrix: 0
processSoundFunctionsDir: {'../processSoundFunctions/'}
frameSize: 5
gd: [1x100 double]
fm: [100x1 double]
cochleaFrequency: 22400
onderwerpen
Beluister het inputsignaal.
opdracht At = 120 ms sprake van een
vrij scherpe overgang? Wat is daar de fysische reden voor?t = 175 ms de frequentie van de
formanten. Dit is het gemakkelijkst door een doorsnede op dit
tijdstip (framenummer 35) te plotten:
global D
figure, plot(D.EdB(:,35))
Fmax) op 10.000 Hz,
bereken en plot een cochleogram met
plotProcessSound en bereken vervolgens een
FFT-spectogram:
[x fs] = wavread('wav/nul.wav');
nfft = 256;
stepT = env.frameSize;
windowName = 'hanning';
PLOT = 1;
figure
[S, SInfo] = fftGram(x, fs, nfft, stepT, windowName, PLOT);
nfft. Wat betekent dit voor de
windowgrootte en daarmee voor de temporele resolutie?t = 175 ms (frame 35).
figure
subplot(2,1,1); plot(D.EdB(:,35));
set(gca, 'xdir', 'reverse'); grid on;
xlabel('segment nummer');
title('Cochleogram doorsnede op t = 175');
subplot(2,1,2); plot(SInfo.F, S(:,35));
axis([0 6000 -inf inf]); grid on;
xlabel('Freq in Hz');
title('FFT-spectrum voor t = 175')
nfft van 256 en
512. env.fm(100).
Zet, zo nodig, het aantal segmenten weer op 100, kies als hoogste
frequentie Fmax 4000 Hz, en bereken een
cochleogram met daarin de NSC's van het harmonische complex van de
klank. Dit kun je doen door HCBits te
selecteren uit de functielijst. Kies ook plotProcessSound,
zodat het cochleogram wordt geplot. Dit levert
onder andere een variabele CHH op, met daarin allerlei informatie,
waaronder de NSC's (signaalcomponenten) waaruit het harmonisch complex
bestaat. Harmonische complexen worden bepaald door eerst alle horizontale signaalcomponenten (tonen) te zoeken, en vervolgens te kijken of er een harmonische relatie is tussen sommige van deze tonen. Als er een harmonische relatie wordt gevonden wordt er een CHH gemaakt, waarin de signaalcomponenten staan waaruit dit harmonisch complex is opgebouwd. Hieronder een aantal velden uit eem voorbeeld van de variabele CHH. (Het aantal harmonische complexen, dus het aantal CHH's dat wordt gevonden is afhankelijk van de geluidsfile die je verwerkt.)
N.B. De variabelen D, NSC en CHH zijn niet altijd per default
beschikbaar. Wanneer een variabele onbekend is, maak deze dan
globaal met global D NSC CHH, afhankelijk van
welke variabelen je uitgerekend hebt.
CHH =
1x13 struct array with fields:
nsc
fr
harm
f0
score
onsetNSC
segmentOffset
rms
startIndex
startFrame
sn
det
pearsonCorr
In een CHH kan je o.a. vinden welke NSC's deze CHH is opgebouwd. Vervolgens kan je in de NSC variable weer meer vinden over deze NSC's, bijvoorbeeld:
ans =
fr: [1x79 double]
seg: [1x79 double]
L: 79
salience: 2
type: 0
freq: [1x79 double]
EdB: [1x79 double]
PAS: [1x79 double]
medianFreq: 113.3302
Wanneer er sprake is van een enkele spraakklank in een geluidsfile, dan zullen er niet veel CHH's zijn waar informatie instaat. Je kunt de niet-lege CHH's vinden door diegene te selecteren die een positieve score hebben:
find([CHH.score] > 0)
Wanneer je de juiste CHH hebt gevonden, kan je de fundamentele frequentie f0 en de bijbehorende NSC's plotten in het cochleogram:
hold on
plot(CHH(9).fr, freq2seg(CHH(9).f0), 'k', 'LineWidth', 3)
for ii = CHH(9).nsc'
plot(NSC(ii).fr, NSC(ii).seg, 'w', 'LineWidth', 3)
end
opdracht B
figure
plot(CHH(9).fr, CHH(9).f0)
grid on
We kunnen de frequenties van de NSC's die een CHH opbouwen
plotten en bovendien kunnen we, wanneer we de frequentie door het
harmonische nummer delen, zien wat de "mening" van elk van de
harmonischen is over de fundamentele frequente f0.
N.B. De NSC's die de harmonischen voorstellen komen niet perse
overeen met onderstaande lijst. Afhankelijk van de instellingen
vindt de functie meer over minder NSC's. Check dus voor je eigen
signaal welke NSC's overeenkomen met welke harmonischen. Een
makkelijke manier om dit te checken is in
D.NSC_S, via figure,
imagesc(D.NSC_S). Wanneer je vervolgens met de
datacursor over de gekleurde NSC's gaat kun je zien welk index
nummer ze hebben. Vergelijk deze NSC nummers met de NSC's in de CHH.
figure
for ii = 1:length(CHH(9).harm)
nsc = CHH(9).nsc(ii);
t = NSC(nsc).fr * env.frameSize/1000;
freq = smooth(seg2freq(NSC(nsc).seg));
subplot(1,2,1); hold on
plot(t, freq)
subplot(1,2,2); hold on;
plot(t, freq/CHH(9).harm(ii))
end
subplot(1,2,1); axis tight; box on;
xlabel('Tijd in sec'); ylabel('Freq in Hz');
title('Frequentieontwikkeling harmonischen');
grid on;
subplot(1,2,2); axis tight; box on;
xlabel('Tijd in sec'); ylabel('Freq in Hz');
title('Schatting f_0')
grid on;
Wat opvalt in het rechter plaatje, is dat de frequenties niet echt
mooi op elkaar passen, maar dat er sprake lijkt te zijn van een
systematische fout. De lagere harmonischen (die, afgezien van de
tweede harmonische, in tijd later ophouden) zijn ten opzichte van
de hogere harmonischen iets verschoven naar latere
tijdstippen. Dit is een effect van group delay (zie voor
uitgebreide uitleg proefschrift H 3.2,
onderaan pagina 88). De group delay is al uitgerekend en
opgeslagen in env.gd. Omdat de GD segmentafhankelijk
is, moet er ook segmentsgewijs voor worden gecorrigeerd. Dit
gebeurt in de regel met GD correctie. Hierin is
env.gd(seg) de GD correctie in ms. Wanneer dit
gedeeld wordt door env.frameSize krijg je een
correctie in frames. Een en ander geeft nu:
figure
for ii = 1:length(CHH(9).harm)
nsc = CHH(9).nsc(ii);
frGDcor = NSC(nsc).fr - env.gd(round(NSC(nsc).seg))/env.frameSize;
t = frGDcor * env.frameSize/1000;
freq = smooth(seg2freq(NSC(nsc).seg));
subplot(1,2,1); hold on
plot(t, freq)
subplot(1,2,2); hold on;
plot(t, freq/CHH(9).harm(ii))
end
subplot(1,2,1); axis tight; box on;
xlabel('Tijd in sec'); ylabel('Freq in Hz');
title('Frequentieontwikkeling harmonischen');
grid on;
subplot(1,2,2); axis tight; box on;
xlabel('Tijd in sec'); ylabel('Freq in Hz');
title('Schatting f_0')
grid on;
opdracht C
env.gd.t = 200
ms en de bijbehorende fout. Gebruik hiervoor de
zoom-functie in Matlab.
figure
[x fs] = wavread('wav/nul.wav');
nfft = 512;
stepT = env.frameSize;
windowName = 'hanning';
PLOT = 0;
[S, SInfo] = fftGram(x, fs, nfft, stepT, windowName, PLOT);
fr = round(200/SInfo.stepT);
plot(SInfo.F, S(:,fr)); axis([0 2000 -30 40])
xlabel('Freq in Hz');
grid on;
t = 200
ms. Maak op basis hiervan een alternatieve schatting van de
fundamentele frequentie met bijbehorende fouten. Leg uit en
onderbouw of deze schatting even nauwkeurig kan worden.
Tot slot gaan we even wat beter kijken naar de plaats-frequentie
relatie en de group delay (GD) die respectievelijk in
env.fm en env.gd opgeslagen zijn.
GD is een vertraging die samenhangt met de frequentiespecificiteit van de segmenten van (de plaats op) de cochlea. Des te meer een segment zich specialiseert op een beperkt frequentie gebiedje, des te langer duurt het voordat het systeem heeft 'besloten' hoe het moet reageren op input. Grotere frequentie specificiteit leidt dus tot een vertraging (zie proefschrift 3.2). Met onderstaande commando's worden de GD en de plaats-frequentie relatie op een aantal manieren gevisualiseerd.
figure
subplot(2,2,1);
plot(1:length(env.gd), env.gd); grid on;
title('Group delay als fie van segm. #')
ylabel('GD in ms')
subplot(2,2,2);
plot(env.fm/1000, env.gd, env.fm/1000, 10*1000./env.fm); grid on;
legend({'Group delay', 'GD~10/(BF)'}, 1)
axis([0 env.fm(1)/1000 0 env.gd(end)]);
title('Group delay als fie van best freq.')
xlabel('Best freq. in kHz')
ylabel('GD in ms')
subplot(2,2,3);
plot(1:length(env.fm), env.fm/1000); grid on;
title('Plaats frequentie-relatie')
xlabel('Segment nummer')
ylabel('Best Freq in kHz')
subplot(2,2,4);
semilogy(1:length(env.fm), env.fm/1000); grid on;
title('Plaats frequentie relatie')
xlabel('Segment nummer')
ylabel('Best Freq in kHz')
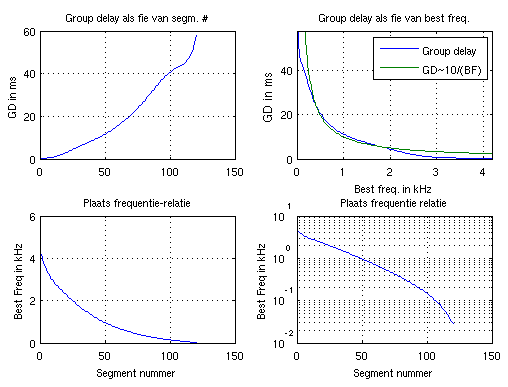
De plaats-frequentierelatie gedraagt zich volgen de zogenaamde Greenwood map (proefschrift H 3.3) en is ongeveer lineair voor frequenties onder de 100 Hz en logaritmisch voor frequenties boven de 400 Hz, daartussen is een overgangsgebied. De groene lijn in de rechterbovenhoek is een benadering van het de relatie tussen de GD en de karakteristieke frequentie (best frequency).
opdracht D
env de combinaties van de
karakteristieke frequentie en de GD voor het eerste segment, het
laatste segment, en een segment halverwege de cochlea. Noteer de
waarden en geef ze aan in bovenstaande subplots.c in formule
3.4 van het proefschrift.Nu gaan we de respons van het systeem op een standaardsignaal bestuderen, namelijk de puls.
Famesize in 1 ms.config van calcEdB
de dynamic range in 90 dB en bereken een cochleogram van de file
puls8kHz.wav met een
uniform referentie spectrum.
Op het eerste gezicht lijkt het alsof een impuls, en dan vooral
aan de laag-frequentie kant, tot een enorm brede excitatie van
meer dan een halve seconde leidt. Maar vergeet niet dat de kleur
codering hier 90 dB is, en dus een factor miljard omvat. In het
lineaire domein is de situatie minder dramatisch. Het is mogelijk
om de impuls respons in lineaire eenheden (opgeslagen in
D.E) van elk 20ste segment te plotten met behulp
van:
figure
fr = 1:300;
plot(fr * env.frameSize, D.E(10:20:end,fr)');
grid on;
title('Impuls respons van segmenten 10:20:100');
xlabel('Tijd in ms');
ylabel('Energie (lineair)');
env.fm(10:20:100)
opdracht E
env.gd
of de grafieken hierboven. Klopt je schatting?We zetten het systeem nu weer op geschikte default waarden voor spraaksignalen:
Framesize weer naar 5 ms.config van calcEdB) weer
terugveranderen naar 60 dB, en het referentie spectrum (onder
config van calcRS) weer terug naar
uniform.
Dit leidt tot een env:
env =
gdCorrection: 0
nseg: 100
maxf: 4000
desiredFrameSize: 5
Qfac: 0.0500
tau: 0
nPeriod: 2
energyCorFac: 1.0000e+10
maxDiff: 0.0050
initdep: 1
amplitudeMatrix: 0
processSoundFunctionsDir: {'.../processSoundFunctions/'}
frameSize: 5
gd: [1x100 double]
fm: [100x1 double]
cochleaFrequency: 22400
Neem in Audacity een zinnetje op met een klein aantal lange
harmonische complexen op. Bijvoorbeeld "Why I owe you
more?". Bereken een cochleogram (via plotProcessSound en
HCBits, zodat ook de NSC's berekend en
geplot worden) van deze zin en sla het resultaat van de NSC's en
CHH('s) op in NSC1 en CHH1.
global NSC CHH;
NSC1 = NSC;
CHH1 = CHH;
opdracht F
plotProcessSound en HCBits tot
CHH2 en CHH3. Neem nu een aantal keer /oe ie aa/ op, maar spreek elke klank vragend (toonhoogte omhoog gaand), of zelfs met een fluctuerende toonhoogte uit, zodat de kans groot is dat een harmonische van de laagste formant op enig moment precies onder het midden van de formant valt.
opdracht G
postadres
Auditory Cognition Group
Kunstmatige Intelligentie
Rijksuniversiteit Groningen
Postbus 407
9700 AK Groningen
bezoekadres
Bernoulliborg
Nijenborgh 9
9747 AG Groningen