New Rule Description: Negotiation

Here we try now to add a new rule to the game: the possibility to negotiate between the pirates. With this we mean that after the proposal, the pirate that would make a proposal in the next turn, can make a counter offer; and after this the first pirate can make his final proposal. To be more clear here is an example: pirates A,B,C,D,E; A makes the first proposal, B the relative counter proposal and A the final proposal. B counter proposal is in the future; this means that he can consider A's death. This gives the opportunity to "change" the future step.
The counter offer will result victorious only if all the pirates, except the two proposing, will accept the proposal. The idea is that thanks to this rule it is possible to influence the future turn with the present one. In the normal game it is always the future step that determinates the outcome or the strategy of the present one; with this rule we want to make possible to do also the opposite. So every pirate can now choose between 3 possible ways: the proposal, the counter proposal, or refuse both and continue to the "normal" future step. Below you can see a map of the possible cases, that help reasoning on the problem.

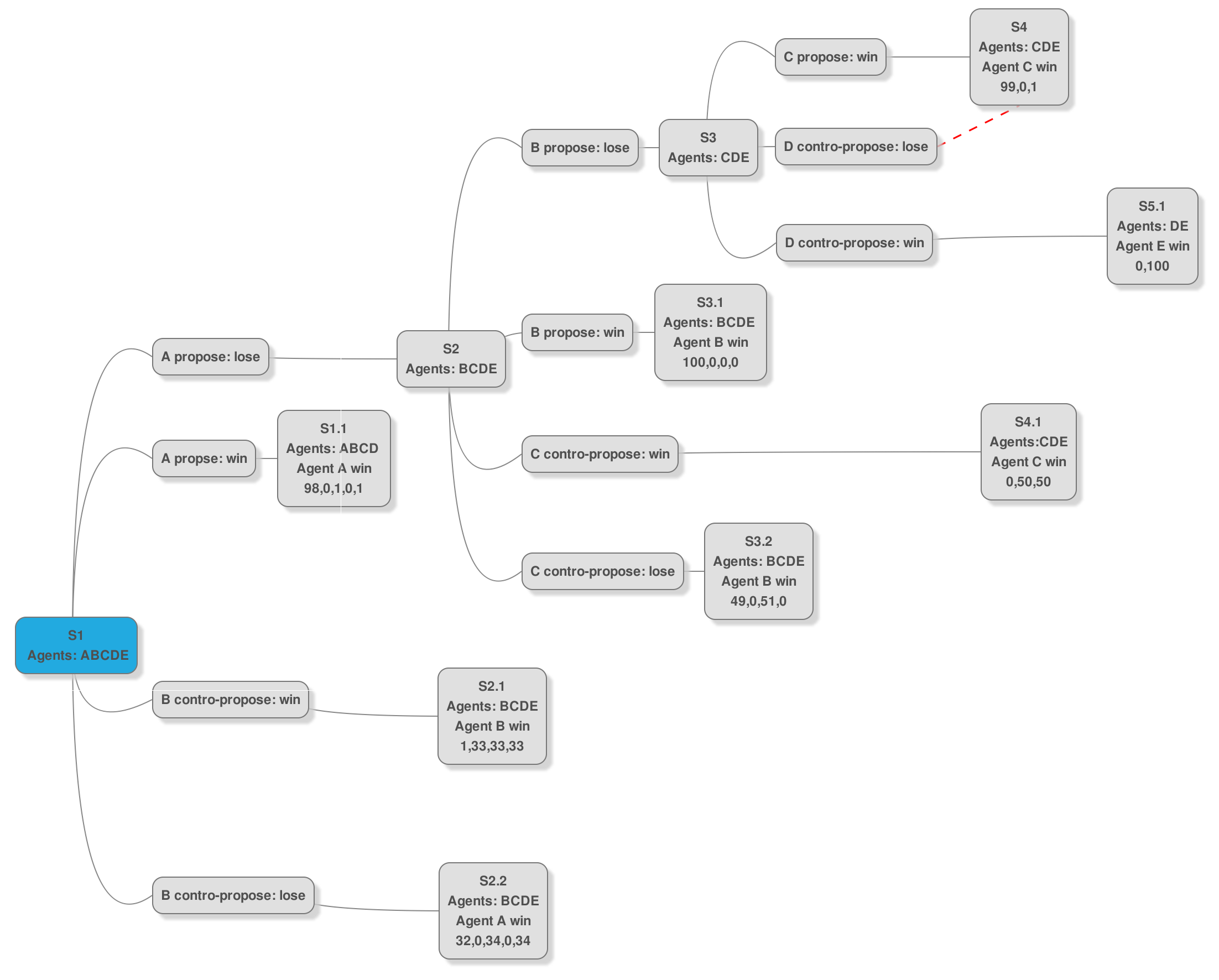
To fully understand this map, it must be noticed that all cases ("S") with the first same number (example "S2.1" and "S2.2") refer to the same "turn". So the second number represents the possibility. So "S2.1" is an alternative solution to "S2.2", in the 2nd turn. Every "turn" is defined by the number of pirates alive.
The new rule introduced complicates the reasoning, since the future step determinates the present one, and, now, also vice versa. In the above map it is not present, but the fisrt end-state is the same as the normal game, with only pirate D and E alive, and the solution 100,0. We called this state "S5". Considering this winning state, we go to the previuos step "S4". This again is the same as the normal rules game. Pirate C first proposes the standard solution: 99,0,1. Now D can make his counter proposal; and for it to be victorious, he needs to convince E. But D also knows that after his proposal, C will make a final one. If for example D proposes 0,98,2; then C will propose 97,0,3. Knowing this, it's impossible for D to earn money; but if D proposes 0,0,100; then C will be obligated to do the same. Now E will choose D's proposal, because of the 3rd rule of the pirates (if possible, kill other pirates). Considered so D will propose 0,0,100; so even if he won't get any money, he will kill C. This solution implies that "S5.1" is the new solution of step 5, and it derives directly from step 4. This also shows that C has no possibility to survive in this step, even if gives away all the money.
Found that there is no solution for step 4 (solution in step 5), let's look at step 3. Here pirate B knows that in the future step pirate C will die no matter what he tries, so he is secure of C positive vote. Since B needs 2 votes for winning, and he knows that since C wants to survive, he can take all the money, relying of C's vote. But the new rule can change, like we said, future states: C makes a control-proposal giving money to both D and E. Like in the previous step, since C needs to convince both D and E to win, and C doesn't want to go to step 4 (where the only solution it's his dead), he will propose 0,0,50,50. Pirate B has the advantage that he needs only to convince one pirate to win; so he will propose 51 to D to obtain his vote, and so to win. Not to E because he will rather got to step "S5.1". So the final state is "S3.2" for step 3.
Following the same reasoning for the previous step, the first A proposal would be "S1.1", that would be victorious with the normal rules. But B can make a control-proposal, and since he needs to convince all the other pirates he will divide all the money between them for the same reasons of the previous steps. Also A has the advantage that he needs to convince only two pirates. So A will choose C and E (pirates that in the future step won't get any money), and gives them more money then B's proposal. So the the winning state is "S2.2". Again A can win immediately, but with a very different amount of money compared to the normal-rules game.