Game and modifications

Game

Kemps is usually played with a standard deck of 52 cards and 2 pairs of people who have the goal to get 4 cards of the same number. The game is played in turns, in each turn the players have to discard an own card and choose a new one between four options to try to achieve the goal. The game ends when a player says either 'kemps' or 'not kemps'. When a player says 'kemps' and his parner has 4 cards of the same number this team wins, if a player says 'not kemps' and one of the opponents has 4 cards of the same number the player who said 'not kemps' and his partner also win the game. In case of a false 'kemps' or 'not kemps' notification the opposite team automatically wins.

Modifications

To reduce the complexity of the game and make it easier to analyze, we decided to make some modifications to the original game. Instead of a standard deck of 52 cards a reduced deck of 10 cards (with 5 pairs of the same number) is used, 2 cards lay face down on the table and the other 8 cards are divided randomly among the 2 pairs of players. When all players can see each others movements, the knowledge about which cards every player has can become common knowledge relatively fast, namely possibly after 2 swaps. Therefore we decided to make the actions of the players partially observable, in the way that players can only see the actions of the player sitting opposite to themselves, see the image below.

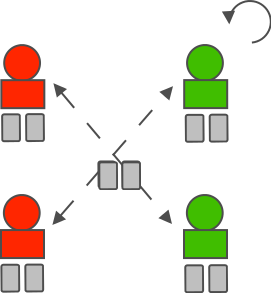
Game after initialization. 2 cards are shown face down on the table, the other 8 cards are divided randomly among 2 pairs of players, shown as a green pair and a red pair. The dashed arrows indicate the players who can see each others movements. The game is played counter-clockwise.

Another modifications is that in our implementation only the player who is on turn may call 'kemps' or 'not kemps', this to avoid that the game will end in a tie (the partner would call 'kemps' at the same time as the opponent(s) would call 'not kemps'). This modification has the consequence that when the first player of a team has two same cards, the second player of the team will call 'kemps' and this team will win the game. However, when the second player of a team has two same cards, the next player will be an opponent player and is likely to say 'not kemps' and therefore these opponents will win the game. So because of this modification it becomes essential for the first player of a team to get two same cards and for the second player to avoid to get two same cards.