Ciarán Lier and Michiel van der Ree

---

Introduction   Methods   Results   Code  Conclusion

---

Methods

To represent the knowledge of the three players we use an S5₍₃₎-model M. This model consists of a set of states S, a truth assignment function π and set of accessibility relations R_i for each player. We represent each R_i by a matrix of truth-values. To show how we update the model once new information is made available, we give a worked example of using matrices of truth-values to represent accessibility relations to analyze the muddy children puzzle.

Worked example: muddy children

We assume the setup of the puzzle is known (if not, find an explanation here). We represent each set of accessibility relations R_i at the start of the puzzle in the following way:

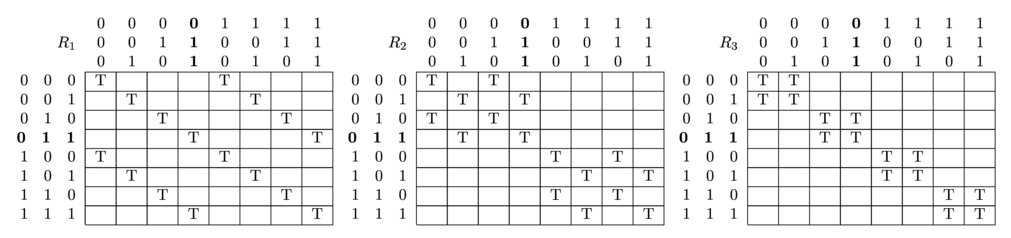
Here, a vector (0,0,1) represents the state in which agents 1 and 2 are clean and agent 3 is muddy. A T (for "true") at a position (s,t) in a matrix should be understood as saying that the agent considers t to be possible in s. In this example, we assume that (0,1,1) is the actual state, i.e. agents 2 and 3 are muddy while agent 1 is clean.

The puzzle starts with the announcement that at least 1 child is muddy. The accessibility relations are then updated in the following way:

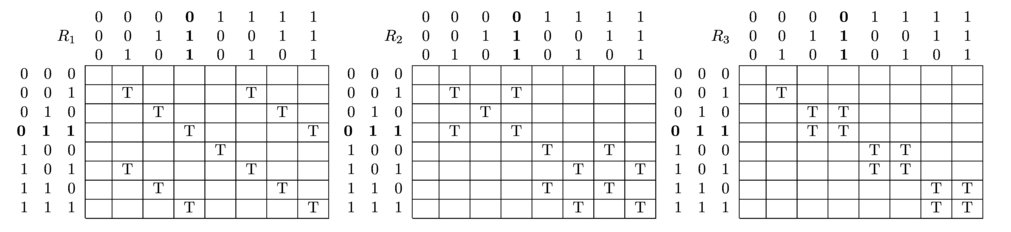
From the mother's announcement all agents know that (0,0,0) is impossible. The model is updated by removing all accessibility relations to and from that state. In the matrices, this amounts to removing all T's in both the row and the column corresponding to the impossible state.

From the semantics of epistemic formulas we know that knowing a certain formula is equivalent to that formula holding in accessible worlds considered possible. Since all states are mutually inconsistent, knowing which state she is in requires an agent to consider only that state possible. From the matrices we can see that each agent still considers multiple states possible in the actual state (0,1,1). When the mother asks whether anyone knows whether she is muddy or not, this implies that nobody will step forward.

The muddy children puzzle is famous for this not-knowing being a source of information in itself. From the matrices, we can see that agent 1 would've known whether she was muddy if (1,0,0) had been the actual state. Similarly, agent 2 would've known whether she was muddy if (0,1,0) had been the true state and agent 3 would've known if (0,0,1) had been the actual state. Since all players now know these states are impossible, all relations to and from those states are removed from the model:

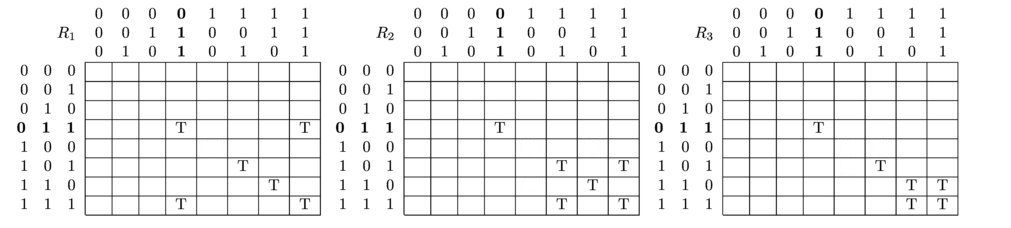
We can see that both agent 2 and agent 3 now know they are muddy: in the actual state, they only consider the actual state possible.

Application to "What's My Number?"

This method of updating a model can also be used to represent the changing knowledge of players' cards in "What's My Number?". The sets of states S consists of all possible distributions of the nine cards over the three players. This amounts to a total of

states. The relations matrices R_i are initialized in such a way that (s,t) ∈ R_i if and only if in states s and t the same cards are assigned to players other than i.

There are two ways in which new information can change the accessibility relation matrices:

1. A player truthfully answers a question. In all matrices, relations to and from states which are now impossible are removed. For example, if player 1 indicates that she only sees odd numbers, all values in the row and column corresponding to states in which she would not only see odd numbers are set to false in all matrices.
2. All players indicate that they do not know their cards yet. Then in all matrices, relations to and from states in which at least one of the players would have known her cards are removed. Similar to the muddy children example, agent i knowing an untruthful state means that there is a state s other than the actual state for which (s,s) is the only true value in both the column and row corresponding to s in R_i.

Experiments

We have ran nine experiments under various conditions. Each experiments consists of 7560 games, which are all different in their true game state. This is the complete collection of possible true game states. The order in which states are used is random but fixed, due to the nature of C++'s random_shuffle algorithm. The same holds for the order of question cards in each game. This allows for easy comparison between games. Note that this does not exhaustively consider all possible game courses, since the stack of question cards is shuffled at the beginning of each game.

We consider the following nine conditions:

1. No epistemagic, standard game
2. No epistemagic, Kooi's Choice using worlds considered possible in true state
3. No epistemagic, Kooi's Choice using full model
4. Epistemagic once, standard game
5. Epistemagic once, Kooi's Choice possible worlds
6. Epistemagic once, Kooi's Choice full model
7. Epistemagic until steady, standard game
8. Epistemagic until steady, Kooi's Choice possible worlds
9. Epistemagic until steady, Kooi's Choice full model

A standard game is a game where the questions are randomly shuffled into the stack and drawn from the top. When no epistemic reasoning is used agents use only direct information from the question answer to cross off possible numbers for their board until only two possibilities remain. Under the epistemagic condition, the S5₃-model is used to infer more information from the fact that other players are not yet able to know their numbers. 'Epistemagic once' means that epistemic step is used once each turn. 'Epistemagic until steady' means that the epistemic step is repeated until the model does not change any more.

Recall that when player's use Kooi's choice, there are two ways to determine the information gain of a question:

• Consider how many of the states considered possible by any of the players in the actual state become impossible.
• Consider how many of the states considered possible by any of the players in any states in the model become impossible.

The outcome of these experiments are listed under results.