Thus, a Kohonen cell is characterized not only by its feature vector representing a single stroke, but also by a number of additional attributes, such as the probability pi that cell i gets a 'hit', and a list of possible stroke interpretations and their likelihood. The concept of stroke interpretation can be explained as follows. In a stroke interpretation code Zn/m, Z represents a letter, n is an integer representing the nth stroke position within the letter, and m indicates that this is an m-stroked letter. Thus a1/3 can be read as: "the first stroke of a three-stroked a". Figure 1 displays a part of the Kohonen SOM of strokes and the attribute lists of a number of cells (i, j and k).
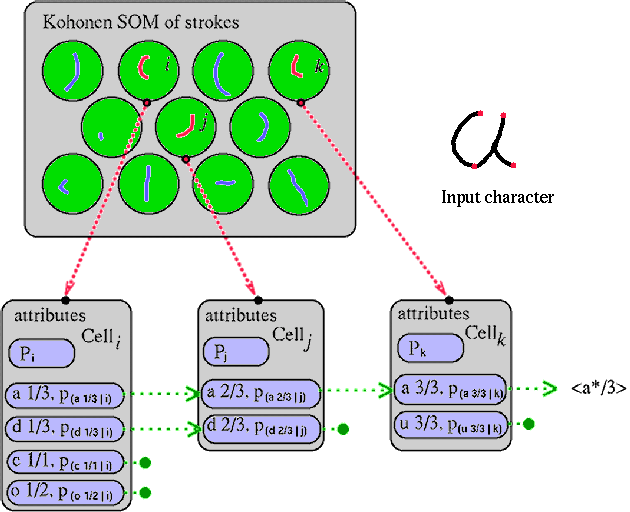
Figure 1. A transition network through a Kohonen self-organized map of velocity-based strokes
The transition network is represented by the dotted green arrows in Figure 1. A path of consistent stroke interpretations can be followed, going from cell i to cell j. Two stroke interpretations are consistent, if they refer to the same character, and if the second stroke is the logical follow-up of the first. So, the stroke transition a1/3 --> a2/3 is logically consistent, whereas the transition d1/3 --> a2/3 is not. When a sequence of stroke interpretations can be followed which represents a full character, a character hypothesis (Z*/m) is emitted. This simple setup makes no use of an actual matrix of transition probabilities, which would be too expensive. The probabilities of a sequence of stroke interpretations representing a full character are combined to yield a quality measure of the resulting character hypothesis. A number of schemes can be envisaged. The product of probabilities for instance, yields low recognition rate results. This is due to the fact that a single, badly-written stroke overrules the good quality of the well-written strokes in such a product-rule approach. Surprisingly, the - theoretically flimsy - average probability ((1/m) Sum p) already yields good results, whereas the best results are obtained with ((1/m) Sum -plogp).
Please refer to our Publications when using anything from the shown material.
to the "NICI stroke-based recognizer of on-line handwriting" page
Handwriting Recognition and Document Analysis Conferences Pen & Mobile Computing NICI Handwriting Recognition Group home page UNIPEN tools Handwriting-related Java demos
Copyright Lambert Schomaker (April 1, 1996)
since 2/Oct/1996