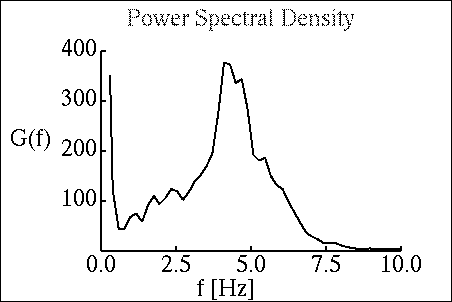
Figure 1. Average PSDF of pen-tip movement in (mixed) handwriting of 32 writers
In this demo, the effects of low-pass filtering of on-line handwriting signals are shown. For speed reasons, we use a digital FIR filter with a boxcar impulse response. In our on-line handwriting recognizers, we mostly use the FFT/IFT method. Before applying any filter, it is essential to know something of the bandwidth of pen-tip movements in handwriting. Of course, we assume an equidistant-time sampled signal (Fs=100Hz).

Figure 1. Average PSDF of pen-tip movement in (mixed) handwriting of 32 writers
There is a peak at about 4 Hz, showing the basic periodicity in handwriting. Figure 1 shows a typical power spectral density function for pen-tip movements in handwriting, averaged over 32 writers, 210 words per writer. The word XY pen-tip displacement time functions were circularized with a cosine transition function and padded with zeros until 512 samples (i.e., about 5s of writing time), and an FFT was calculated for that word. The average power spectrum (power-spectral density function, PSDF) of pen-tip movement over words was calculated by accumulating |FFT|^2. The spectrum shows that from the Nyquist sampling theorem point of view, a sampling frequency of 20 samples/second would be sufficient for reconstruction of the signal. However, it is much cheaper to use higher sampling rates than to reconstruct the trajectory and display it in real time. A sampling frequency of 100 samples/second yields about 10 points per stroke in normal handwriting. Five points per stroke is the (barely) acceptable minimum, for users of pen computers.
Please refer to our Publications when using anything from the shown material.

Notes:

 to NICI's Java-based Handwriting Demos page
to NICI's Java-based Handwriting Demos page
 to NICI's on-line handwriting recognizer description
to NICI's on-line handwriting recognizer description

 Handwriting Recognition and Document Analysis Conferences
Handwriting Recognition and Document Analysis Conferences  Pen & Mobile Computing
Pen & Mobile Computing  NICI Handwriting Recognition Group home page
NICI Handwriting Recognition Group home page  UNIPEN tools
UNIPEN tools

Copyright Lambert Schomaker (April 1, 1996)
since 1/Mar/1996