Leesgroep Epistemische Logica

Verslag

B.P. Kooi

In het boek ‘De Prinses of de Tijger’ van Raymond Smullyan staat het volgende probleem:

Drie proefpersonen - A, B en C - waren allen volmaakte logici. Elk van hen kon ogenblikkelijk alle gevolgtrekkingen maken uit een reeks vooronderstellingen. Ook wist ieder dat elk van de anderen een volmaakt logicus was. Deze drie kregen zeven zegels te zien: twee rode, twee gele en drie groene. Toen werden ze geblinddoekt, en er werd op ieders voorhoofd een zegel geplakt; de overblijvende zegels werden in een lade gelegd. Toen de blinddoeken afgenomen waren, werd aan A gevraagd: ‘Weet je één kleur die je zeker niet hebt?’ A antwoordde: ‘Nee.’ B werd dezelfde vraag gesteld en hij antwoorde: ‘Nee.’ Is het mogelijk uit deze informatie de kleur van de zegel van A af te leiden, of die van B, of die van C?

Het was de bedoeling dat het probleem op te lossen door zoveel mogelijk werk aan de Logics Work Bench over te laten. Het project bestond globaal uit twee onderdelen:

1. Alle relevante informatie over de zegels, wat A,B en C van elkaar weten en dergelijke in logische formules weergegeven, zodat de Logics Work Bench die zou kunnen interpreteren.

2. Met de Logics Work Bench zou je een aantal interessante vragen beantwoorden. Is de formalisatie goed gelukt? Welke axioma’s heb je nodig om de afleidingen te kunnen maken? Het is ‘common knowledge’ dat A niet weet welke kleur zij zeker niet heeft. Wat is de ‘intentiediepte’ die je nodig hebt om de afleidingen te kunnen maken. etc.

Voor het eerste deel van de opdracht had ik het volgende bestand gemaakt:

load(s4n);

een_hoed_per_hoofd := [(roodA & ~geelA & ~groenA) v( ~roodA & geelA & ~groenA) v (~roodA & ~geelA & groenA), (roodB & ~geelB & ~groenB) v (~roodB & geelB & ~groenB) v (~roodB & ~geelB & groenB), (roodC & ~geelC & ~groenC) v (~roodC & geelC & ~groenC) v (~roodC & ~geelC &groenC)];

slechts_twee_gele_en_rode := [~(roodA & roodB & roodC), ~(geelA & geelB & geelC)];

wie_ziet_wat := [roodA -> (box2 roodA & box3 roodA), geelA -> (box2 geelA & box3 geelA), groenA -> (box2 groenA & box3 groenA), roodB -> (box1 roodB & box3 roodB), geelB -> (box1 geelB & box3 geelB), groenB -> (box1 groenB & box3 groenB), roodC -> (box1 roodC & box2 roodC), geelC -> (box1 geelC & box2 geelC), groenC -> (box1 groenC & box2 groenC)];

situatie := [(dia1 roodA & dia1 geelA & dia1 groenA), (dia2 roodB & dia2 geelB & dia2 groenB)];

tmp1 := concat(een_hoed_per_hoofd, slechts_twee_gele_en_rode);

niemand_heeft_iets_gezegd := concat(tmp1, wie_ziet_wat);

hoedenprobleem := concat(niemand_heeft_iets_gezegd, situatie);

Bij dit bestand zaten nog enkele vragen, helaas heeft de Logics Workbench hierop geen antwoord gegeven. Vandaar dat ik zal proberen ‘met de hand’ enkele antwoorden te krijgen. Hiervoor zal ik proberen in de logica KEC₍₃₎ het antwoord proberen af te leiden. Hiervoor moet het bovenstaand bestand vertaald worden naar de officiële logische taal.

a. (Ra Ù ¬Ya Ù ¬Ga) Ú (¬Ra Ù Ya Ù ¬Ga) Ú (¬Ra Ù ¬Ya Ù Ga)

b. (Rb Ù ¬Yb Ù ¬Gb) Ú (¬Rb Ù Yb Ù ¬Gb) Ú (¬Rb Ù ¬Yb Ù Gb)

c. (Rc Ù ¬Yc Ù ¬Gc) Ú (¬Rc Ù Yc Ù ¬Gc) Ú (¬Rc Ù ¬Yc Ù Gc)

d. ¬(Ra Ù Rb Ù Rc)

e. ¬(Ya Ù Yb Ù Yc)

f. Ra ® (K_B Ra Ù K_C Ra)

g. Ya ® (K_B Ya Ù K_C Ya)

h. Ga ® (K_B Ga Ù K_C Ga)

i. Rb ® (K_A Rb Ù K_C Rb)

j. Yb ® (K_A Yb Ù K_C Yb)

k. Gb ® (K_A Gb Ù K_C Gb)

l. Rc ® (K_A Rc Ù K_B Rc)

m. Yc ® (K_A Yc Ù K_B Yc)

n. Gc ® (K_A Gc Ù K_B Gc)

o. M₁ Ra Ù M₁ Ya Ù M₁ Ga

p. M₂ Rb Ù M₂ Yb Ù M₂ Gb

P={Ga, Gb, Gc, Ya, Yb, Yc} en A={A, B, C}. Er is dus geen sprake van predikatenlogica. De suggestieve namen van de proposities zijn zo gekozen zodat de bewijzen semantisch eenvoudiger te volgen zijn.

Het formele bewijs heeft uiteraard enigszins de structuur van de gedachtengang die je moet hebben om het probleem gewoon op moet lossen. Stel C heeft een rood zegel op haar voorhoofd. Het enige geval waarin A kan weten welke kleur zegel zij niet op heeft, is als B en C allebei een rood zegel op hun hoofd hebben. Als A ontkent dat ze weet welke kleur ze niet heeft weet B dat zij zelf geen rood zegel op haar hoofd heeft. Als haar dus gevraagd wordt of zij zeker weet welke kleur zij niet op heeft kan zij antwoorden: ‘Ik weet zeker dat ik geen rood zegel op mijn heeft heb.’ B zegt echter dat ze niet weet welke kleur zegel ze niet op haar hoofd heeft. Dus is het niet zo dat C een rood zegel op haar hoofd heeft. Een analoge redenering is van toepassing als je je voorstelt dat C een geel zegel op haar hoofd heeft. Als C geen rood en geen geel zegel op heeft, heeft ze dus een groen zegel op haar voorhoofd.

Laat Y de conjunctie zijn van a tot en met p, oftwel Y =aÙ ...Ù p. De situatie is ‘common knowledge’. De vraag is nu of CY ® Gc. (Als achter een regel de rechtvaardiging A1(,..,c ) (_,c Î {a,..,p} staat wordt verwezen naar de relevante formules van Y .

1. CY ® ECY A8

2. CY ® Y A7

3. ECY ® EY ED(2)

4. EY ® (K_AY
ÙK_BY
ÙK_CY) A6

5. (K_AY
ÙK_BY
ÙK_CY) ® K_AY A1

6. Y ® ((RbÙ Rc)® ¬Ra) A1(d)

7. K_AY
®K_A((RbÙ Rc)® ¬Ra) KD(6)

8. K_A((RbÙ Rc)® ¬Ra) ® (K_A(RbÙ Rc) ® K_A¬Ra) A2’

9. CY ® (K_A(RbÙ Rc) ® K_A¬Ra) HS(1,3,4,5,7,8)

10. Y ® ((RbÙ Rc) ® (K_ARb Ù K_ARc)) A1(i,l)

11. CY ® ((RbÙ Rc) ® (K_ARb Ù K_ARc)) HS(2,10)

12. Rb ® (Rc ® (Rb Ù Rc)) A1

13. K_ARb ® K_A(Rc ® (Rb Ù Rc)) KD(12)

14. K_A(Rc ® (Rb Ù Rc)) ® (K_ARc ® K_A(Rb Ù Rc))) A2’

15. K_ARb ® (K_ARc ® K_A(RbÙ Rc)) HS(13,14)

16. (K_ARb ® (K_ARc ® K_A(Rb Ù Rc))) ® ((K_ARb Ù K_ARc) ® K_A(Rb Ù Rc)) A1

17. (K_ARb Ù K_ARc) ® K_A(Rb Ù Rc) MP(15,16)

18. ((K_ARb Ù K_ARc) ® K_A(Rb Ù Rc)) ® (((Rb Ù Rc) ® (K_ARb Ù K_ARc)) ® ((Rb Ù Rc) ® K_A(Rb Ù Rc))) A1

19. ((RbÙ Rc) ® (K_ARb Ù K_ARc)) ® ((Rb Ù Rc) ® K_A(Rb Ù Rc)) MP(17,18)

20. CY ® ((Rb Ù Rc) ® K_A(Rb Ù Rc)) HS(11,19)

21. (CY ® ((RbÙ Rc) ® K_A(RbÙ Rc))) ® ((CY ® (K_A(Rb Ù Rc) ® K_A¬Ra)) ® (CY ® ((Rb Ù Rc) ® K_A¬Ra))) A1

22. (CY ® (K_A(Rb Ù Rc) ® K_A¬Ra)) ® (CY ® ((Rb Ù Rc) ® K_A¬Ra)) MP(20,21)

23. CY ® ((Rb Ù Rc) ® K_A¬Ra) MP(8,22)

24. ((Rb Ù Rc) ® K_A¬Ra) ® (¬K_A¬Ra ® (Rc ® ¬Rb)) A1

25. CY ® (¬K_A¬Ra ® (Rc ® ¬Rb)) HS(23,25)

26. Y ® ¬K_A¬Ra A1(o)

27. CY ® ¬K_A¬Ra HS(2,26)

28. (CY ® (¬K_A¬Ra ® (Rc ® ¬Rb))) ® ((CY ® ¬K_A¬Ra) ® (CY ® (Rc ® ¬Rb))) A1

29. (CY ® ¬K_A¬Ra) ® (CY ® (Rc ® ¬Rb))) MP(25,28)

30. CY ® (Rc ® ¬Rb) MP(27,29)

31. ECY ® (K_ACY Ù K_BCY Ù K_CCY ) A6

32. (K_ACY Ù K_BCY Ù K_CCY ) ® K_BCY A1

33. K_BCY ® K_B(Rc ® ¬Rb) KD(30)

34. K_B(Rc ® ¬Rb) ® (K_BRc ® K_B¬Rb) A2’

35. (K_BRc ® K_B¬Rb) ® (¬K_B¬Rb ® ¬Rc) A1

36. CY ® (¬K_B¬Rb ® ¬Rc) HS(1,31,32,33,34,35)

37. Y ® ¬K_B¬Rb A1(p)

38. CY ® ¬K_B¬Rb HS(2,37)

39. (CY ® (¬K_B¬Rb ® ¬Rc)) ® ((CY ® ¬K_B¬Rb) ® (CY ® ¬Rc)) A1

40. (CY ® ¬K_B¬Rb) ® (CY ® ¬Rc) MP(36,39)

41. CY ® ¬Rc MP(38,40)

...

42. CY ® ¬Yc op analoge wijze af te leiden als CY ® ¬Rc

43. Y ® ((¬Rc Ù ¬Yc) ® Gc) A1

44. CY ® ((¬Rc Ù ¬Yc) ® Gc) HS(2,43)

45. (CY ® ((¬Rc Ù ¬Yc) ® Gc)) ® ((CY ® ¬Rc) ® ((CY ® ¬Yc) ® (CY ® Gc))) A1

46. (CY ® ¬Rc) ® ((CY ® ¬Yc) ® (CY ® Gc)) MP(44,45)

47. (CY ® ¬Yc) ® (CY ® Gc) MP(41,46)

48. CY ® Gc MP(42,47)

Het resultaat is bereikt. Uit de informatie valt af te leiden dat C een groen zegel op zij voorhoofd heeft. De axioma’s A4 (positieve introspectie) en A5 (negatieve introspectie) zijn niet nodig om dit uit de informatie af te leiden.

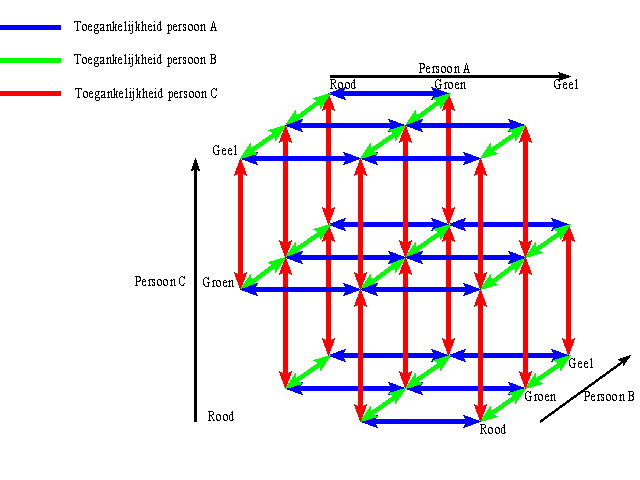
Uit de informatie is de kleur van het zegel van A of de kleur van het zegel van B niet af te leiden. Als je het probleem met behulp van Kripkemodellen probeert op te lossen, kan je dit zien. De situatie voordat iemand iets gezegd heeft kan als volgt in een Kripkemodel worden weergegeven.

De pijltjes vanwege reflexiviteit en transitiviteit zijn weggelaten. In dit model zijn de formules a,...,n van Y waar.

Als nu A zegt dat zij niet weet welke kleur zegel zij niet heeft vallen vier werelden uit.

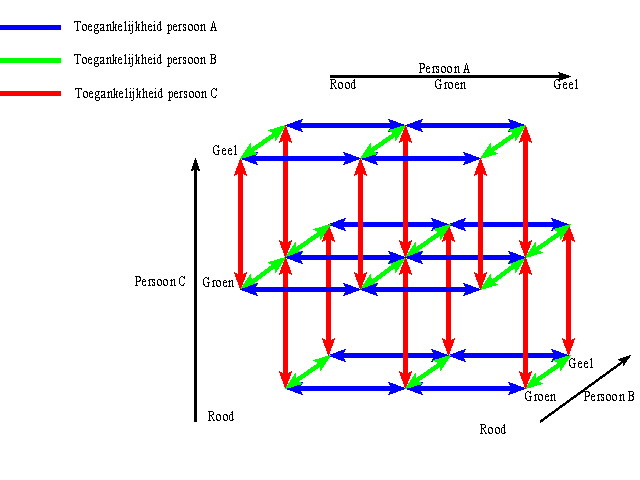
In de werelden die uit zijn gevallen wist A zeker dat zij geen rood had omdat zowel B als C een rood zegel hadden of dat zij geen geel had omdat zowel B als C een geel zegel hadden. Dit was te zien aan de toegankelijkheidsrelatie van A. In dit model zijn de formules a,...,o van Y waar.

Als nu B ook nog zegt dat zij niet weet welke kleur zij heeft vallen er twaalf werelden af.

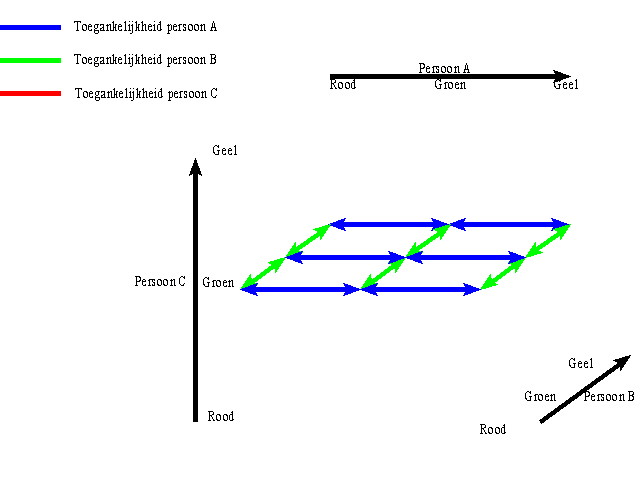
In de werelden die uit zijn gevallen wist B dat zij niet de kleur had die C had. Dit was het geval als C een rood zegel had of een geel zegel. In dit model zijn de formules a,...,p van Y waar, oftewel Y is waar in dit model. In dit model is het zo dat in iedere wereld C een groen zegel heeft. Voor A en B geldt echter dat alle kleuren nog mogelijk zijn. Dus is uit de informatie niet af te leiden wat de kleuren van de zegels van A en B zijn.