Eerste modellen [
top | bekijk
modellen ]
De eerste twee modellen geven de mogelijke
werelden, wat betreft oplossingen weer per persoon, vóór het gesprek tussen
Sam en Pro. Dat wil zeggen, ze hebben beide alle informatie gekregen -
van de Stem - en weten respectievelijk de som en het produkt van de twee
getallen. Het eerste model is het model van Pro, het tweede model is het
model van Sam.
Pro en Sam hebben nog niet met elkaar gesproken en kunnen dus nog geen
onderscheid maken tussen de verschillende mogelijke werelden. Voor Pro
zijn er maar twee mogelijke werelden, namelijk "2 x 26" en "4
x 13". Verder zijn er geen mogelijke productparen, gegeven dat Pro
het getal "52" te horen heeft gekregen. Bij Sam zijn er uiteraard
meer mogelijkheden.
Iedere losse wereld in Sam zijn model, levert weer opties voor wat pro
te horen heeft gekregen (volgens Sam).
Bijvoorbeeld: de wereld "2 + 15" levert het produkt 30
op, de wereld "3 + 14" levert 42 etc. Dus volgens Sam kan Pro
"30" en "42" etc. gehoord hebben van de Stem.
Maar daar houdt de redenatie van Sam nog niet op. Voor elk produkt kan
Sam namelijk ook weer bedenken welke opties Pro dan kan beredeneren. (Let
op: één van de getallenparen is natuurlijk het antwoord!)
Bijvoorbeeld: voor het produkt "30" kan Sam berederenen,
dat als Pro dat produkt heeft gehoord, dat
Pro dan de opties "2 x 15", "3
x 10" en "5 x 6" openhoudt als getallenparen. Zo kan Sam
doorredeneren voor al zijn mogelijke werelden en produkten.
Het gesprek
[ top ]
In dit geval is het zo, dat iedere wereld die Sam voor mogelijk houdt,
weer meerdere opties overlaat voor Pro (in de redenatie van Sam!). Dit
is de reden dat Sam in stap 2 kan zeggen "Ik wist al dat jij het
niet wist". Immers: welk van de mogelijkheden het ook is, er zijn
altijd meerdere mogelijkheden en Pro zal dus nooit met zekerheid een keuze
hebben kunnen maken. In feite is stap 1 dus niet echt interessant, want
Sam had ons meteen wel kunnen vertellen dat Pro het nog niet weet. Na
stap 2 echter, ontstaat een bijzondere situatie. Nu Pro namelijk gehoord
heeft dat Sam een som heeft waarvoor geldt dat voor ieder sompaar produkt
van dat sompaar niet eenduidig is ("p"), kan hij een keuze maken
tussen de twee (!) opties die hij heeft. [ ga
verder ]
 |
Pro vóór stap 1 |
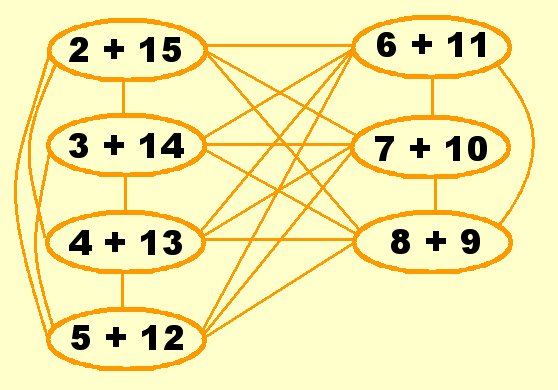 |
Sam vóór stap 1 |
Tweede modellen [ top | bekijk modellen ]
De tweede modellen geven de werelden en relaties weer na de eerste 3 respectievelijk 2 zinnen voor Sam en Pro.
Pro weet na de eerste twee stappen dus dat p geldt voor het getal dat Sam gehoord heeft. Volgens Pro kan Sam slechts twee getallen gehoord hebben van de Stem, te weten "28" of "17". Vandaaruit kan Pro beredenen wat Sam aan opties kan bedenken.
Bijvoorbeeld: voor het getal 28 kan Pro beredeneren, dat Sam de opties: "2 + 26", "3 + 25" .... "14 + 14" heeft. Nu wordt het echter belangrijk, want voor precies één produktpaar van Pro geldt dat de som van dat produktpaar de eigenschap p heeft ("q"). De eigenschap "p" geldt niet als er een combinatie van twee priemgetallen in het rijtje mogelijke somparen staat. Dit is het geval bij de somparen voor 28 (namelijk 11 en 17). Bij de somparen van 17 komt dit niet voor. Nu geldt dus dat voor precies één produktpaar geldt dat de som van dat produktpaar de eigenschap p heeft. Pro weet nu dus de oplossing: 4 x 13!
Nu kan Sam ook een keuze maken, aangezien het getal dat Pro heeft gehoord aan de eigenschap q voldoet. Pro heeft namelijk gezegd dat hij de oplossing weet en hieruit kan Sam afleiden dat er slechts één van de zeven somparen ook aan q kan voldoen.
De nieuwe modellen zijn nu zo, dat zowel Pro als Sam weten welke de oplossing is. Hierdoor zijn er ook geen relaties meer tussen de 'oplossing-wereld' en de andere werelden, omdat zij deze wereld nu kunnen onderscheiden van de andere.
 |
Pro na stap 1 en 2 |
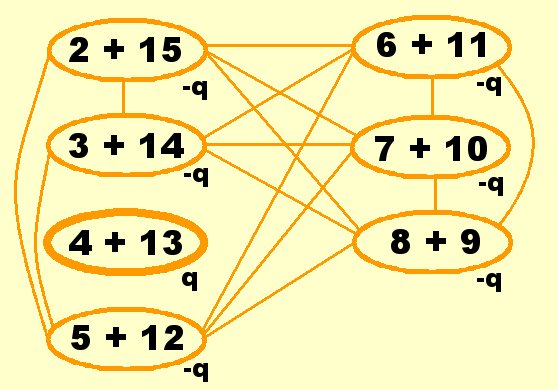 |
Sam na stap 1, 2 en 3 |
Conclusie [ top
]
Sam en Pro zijn nu beide erg gelukkige mensen.
Ze hebben hun grote probleem nu opgelost!
Gelukkig kunnen ze nu weer rustig verder leven. Hoera, hoera, hoera!!
 Sam weet het!
Sam weet het!