---

Logics of WIDM

Epistemic Logic can be used to reason about knowledge and belief in multi-agent systems. The semantics can be represented using a Kripke model. Such a model contains one or more possible worlds and in each of these possible worlds a different validation can be given to each of the propositional atoms in the model.

A Kripke model also contains accessibility relations for the different agents for all the worlds. Belief is then defined using an accessibility relation for belief: agent i in world m believes p iff for all n in M with (m, n) in the accessibility relation, p holds.

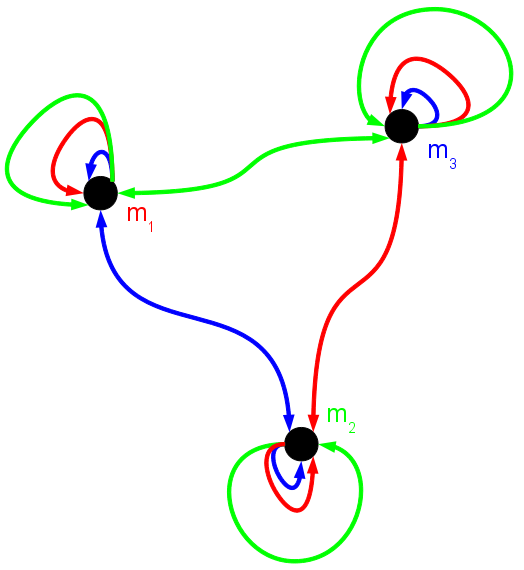
Figure 1 shows a Kripke model for Who Is The Mole with three agents. Any agent playing WIDM has to consider multiple possible worlds in which different properties hold for its competitors. Let m_i, with i = 1,2,...,n be our set of propositions, denoting that i is the mole, then the model consists of n possible worlds, where n is the number of agents. The worlds are labeled m1, m2 and m3. In this case, any world mi validates the proposition mi which means: agent i is the mole. In each of these worlds, another agent is the mole. In the figure, propositions that have a false valuation are not drawn.

The different colored arrows correspond to accessibility relations for the agents 1 (red), 2 (green) and 3 (blue). The background knowledge restricts the accessibility for the agents in two ways: 1. Contestants Since contestant x always knows that he is not the mole and therefore does not consider it to be possible that he is the mole if he is not, he doesn't have any accessibility relation towards world m_x. 2. Mole Since the mole knows he is the mole, and he knows there is only one mole, he does not consider any of the other agents to be possible moles. Since only one agent can be the mole and every agent knows whether he is the mole or not, the two agents that are not the mole are left with a dilemma.

Probabilistic Epistemic Logic

This dilemma has to be solved when an agent actually wants to play the game. No conclusion can be drawn from the model in figure 1. It very clearly models what every agent beliefs and considers possible, but it does in no way answer the vital question: who is the mole?

To solve this question somehow we need to rule out possible worlds. To do this we need additional information. The only property that distinguishes the different worlds is the truth value of the propositions m_i (for i=1,2,...,n). Unfortunately, this value is not visible to the agents. Therefore they will not only have to consider different possible worlds, but also consider some of these worlds are more probable.

Uncertainty

This is where WIDM gets interesting, there are uncertainties in game. First of all, the outcome of working on an assignment is uncertain. The agents can only decide if they want to try or not. Succeeding is a function of trying, the difficulty of the assignment and some random noise. Therefore, the agents need to incorporate the probability that an agent is not sabotaging, but simply failing.

Another uncertainty comes from the behavior of the agents. The mole may be prone to sabotage, but other agents may also want to raise suspicion. This means that if someone is sabotaging, it may be he is not the mole anyway.

To deal with these uncertainties, the agents need to use probabilities. For every world they consider possible, they need a measure of how probable this world is. When answering the question: ``Who is the mole?'', they answer with the most probable mole according to their current belief. The combination of logical reasoning and possible worlds with different probabilities are the main challenge in this simulation.

Two structures

Every agent captures its knowledge and belief in two different structures. The first one contains the probabilistic belief in possible worlds. Every agent has a probability distribution over all other agents denoting to what extend they believe every other agent to be the mole. This is represented in the software as a bar graph, but can also be seen as a Kripke model with weighted accessibility relations. The second structure contains knowledge about what other agents believe. For every competing agent i this agent saves recent knowledge about the most probable mole according to i

Belief and Knowledge updates

During the various phases of a round the belief and knowledge of an agent are updated according to new information.

During the assignment, belief about other agents being the mole is updated: if they see an agent sabotage, this agent becomes more suspicious. If they see an agent succeed, this agent becomes less suspicious.

During the conversations, knowledge about other agents' beliefs is updated. Agents are modeled to tell the truth about the mole they consider the most probable one. Except of course the mole himself, who will lie.

Finally, in the elimination, agents acquire the knowledge that the eliminated player was not the mole. Little use as this may be to them (since it is common knowledge), it may help them indirectly: if they learned during the conversations whom the eliminated player suspected, they can rule out the possibility that this suspicion was correct, and thus update their belief on this person being the mole by setting its probability to zero.