Project Scaled Cluedo

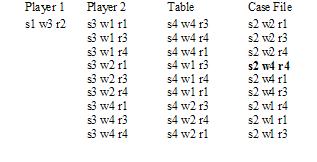
In our project, we create the scaled Cluedo game simplified to 2 players, 4 possible suspects, 4 possible weapons and 4 rooms. Each player is dealt 3 cards and the extra 3 cards are placed face down on the table. The actual murderer, murder weapon and room cards are put into the case file (an envelope). The cards we use are the following:

One player may ask a question that always consists of 1 suspect, 1 weapon and 1 room, to the other player. If the other player has at least one of these requested cards, he will show one card to the suggested player. If none of these cards can be shown, the suggested player may choose to exchange one card from his hand with one of the face down cards on the table. Three faced down cards are separately placed on the table and the player can decide which category he wants to swap (suspect, weapon, or room). In the initial state of the game, there are 4 × 4 × 4 = 64 possible combinations of the cards in the case file.

At the start of the game, we distribute the cards randomly; 1 suspect, 1 weapon, 1 room cards to each of two players, the table and the case file. Each player knows only 3 cards which he holds that are not in the case file. We consider a situation for playing the game:

• Player 1 has s1, w3, and r2.
• Player 2 has s3, w2, and r3.
• Three cards on the table are s4, w1, r1 and r5.
• The actual answer cards: s2, w4, r4 are in the case file.

If Player 1 suggests “s2, w3, r2” and Player 2 does not show. Player 1 has a chance to see a card on the table and he chooses to swap the suspect category. Then he knows his suggested suspect card s2 is not on the table. He knows s2 must be in the case file. Player 1’s accessible world reduces to 9.

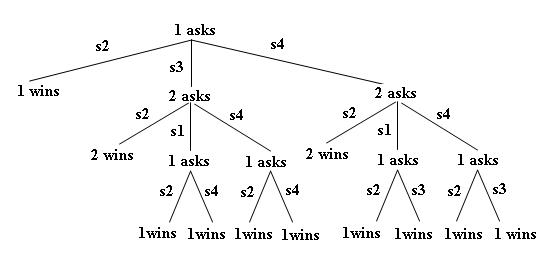
The game tree for the game “Scaled Cluedo” with two players and four suspect cards is shown in the following figure.

Knowledge of the Players

Now, we explain another simplification of the game. We consider the above situation with suspect and weapon cards only.

• Player 1 has s1 and w3.
• Player 2 has s3 and w2.
• s4 and w1 are placed on the table.
• s2 and w4 are placed in the case file.

In this simplification, common knowledge of two players is the following:

• There are 4 suspect cards and 4 weapon cards.
• Every card is unique. One card of each category is dealt to Player 1, Player 2 and face down on the table.
• 1 murderer card and 1 weapon card are placed in the Case File.
• If a player holds a card or he sees a card on the table when he has a chance to swap cards, that card excludes the cards in the Case File.

Assume that the first turn is Player 1’s turn. We can state that the knowledge of the Player 1 about the cards in the case file; K1¬s1 for murderer and K1¬w3 for murder weapon.

Player 1 asks “s2, w3” that consist of one suspect card and one his own card. Player 2 has none of these cards and no show to Player 1. Then, Player 1 has a chance to swap a card on the table. Cards on the table are separated according to category. Swapping can be done by category. Therefore, Player 1 can choose one card he wants to swap; suspect, weapon or room cards. Player 1 swaps his own card, s1 with s4 on the table.

Now, Player 1 knows s1 that was his own card and s4 that was on the table may not be the murderer card. Player 1 updates his knowledge: K1 (¬s1 ˄ ¬s4) for murderer.

Player 1 may know that Player 2 has s3 card because he asked about s2 to Player 2 and Player 2 has not shown s2 card. Therefore, Player 1 knows the actual murderer card is s2. Player 1 updates his knowledge K1 (¬s1 ˄ ¬s4 ˄ ¬s3) --> K1s2 for murderer. However, Player 1 still does not know about weapon card in the case file.

Next is Player 2’s turn. Player 2 knows only his own cards: s3, w2 are not in the case file. Player 2 may assume that one or both of “s2, w3” cards have not been hold by Player 1. Player 2 asks “s1, w1” and Player 1 cannot show any of these cards. Player 2 exchanges his w2 card with w1 card on the table. Then, Player 2 knows that w1 also has not in the case file; K2 (¬w2 ˄ ¬w1).

Then, Player 1’s turn comes again. Player 1 asks about “s2, w2” and Player 2 has any of these cards. Player 1 swaps the w cards on the table and he knows that w2 was on the table. He cannot know whether that card was on the table since the beginning or Player 2 exchanged. But, Player 1 may reason the following facts: Player 2 asked about w1 and w1 was not on the table; so, w1 may be in the case file or in the hands of Player 2. Player 1 updates his knowledge about murder weapon: K1 (¬w3 ˄ ¬w2) --> K1 (w1 ˅ w4).

In Player 2’s turn, he asks “s3, w4” and Player 1 has none of these cards. Now, Player 2 knows that w4 is not in the hands of Player 1 and w4 may be in the case file; K2w4.

In Player 1’s turn, he asks “s4, w1” because he wants to know w1 is in the case file or Player 2 holds. Player 2 shows w1 card and Player 1 knows that w1 is in the hand of Player 2 and w4 is in the case file. Player 1 updates his knowledge about murder weapon: K1 (¬w3 ˄ ¬w2 ˄ ¬w1) --> K1w4.

Now Player 1 knows about the actual murderer and murder weapon. Therefore, Player 1 makes the accusation: “s2, w4” and he wins the game.

If the player is so lucky to deduce the actual murderer and weapons, he can win at any state of the game. At least, he can win if he acts rationally in every turn. If there is an optimal strategy to win the game, he chooses this. However, it is somewhat hard to say for the game like Cluedo.

In our game, we assume that Player 1 represents the user playing the game and Player 2 represents the computer. In this game, Player 1 may use some strategies to win the game about which cards to ask, but Player 2 chooses the suggested cards randomly.