ELPC: Epistemic Logic Proof Checker
by Daniël Wedema
April 13 2011
Introduction
Creating proofs in epistemic logic can often be a challenging task.
For this reason the ELPC program is developed.
ELPC is an epistemic logic proof checker which assists users in building proofs in epistemic logic.
The proof checker does not deal with the semantics of epistemic logic.
It only deals with the derivation of truths in certain systems.
Truth starts with the axioms, i.e. assumptions which are always true.
The derivation rules describe which truths can be derived from already derived formulas.
Epistemic Logic
Intelligent agents have to manage their knowledge.
Some of that knowledge comes from observations of the outside world.
However, smart agents can derive new knowledge based purely on what they already know.
Classical propositional logic deals with propositional facts.
For example the propositions p = 'It is raining' and q = 'The road is wet' are such propositions.
Propositional logic has the basic operators like 'and' (∧), 'or' (∨), 'implies' (→) etc.
(see the list of operators) to combine propositions.
p ∧ q is now read as It is raining and the road is wet.
Modal logic extends these operators by adding the modal operators for 'it is neccesary that' (☐) and 'it is possible that' (◊).
p ∧ ◊q is now read as It is raining and it is possible that the road is wet.
Epistemic logic is a subfield of modal logic that deals with the logic of knowledge.
The modal operator ☐ is interpreted as 'knows' and ◊ is interpretted as 'holds possible'.
In epistemic logic these operators are written as K and M, respectively.
When dealing with multiple agents a subscript is added to indicate which agent's knowledge is referred to.
p ∧ K1q is read as It is raining and agent 1 knows that the road is wet.
The beauty of epistemic logic is that agents cannot only reason about their own knowledge, but also about the knowledge of other agents.
K2K1q is read as agent 2 knows that agent 1 knows that the road is wet.
The operators K and M are the basic operators in epistemic logic.
However, there are extensions of these two with operators for 'everybody knows' (E) and 'it is common knowledge that' (C).
When every agent knows a certain proposition, e.g. Kiq for all i, then it can be said that everybody knows q, i.e. Eq.
When on top of this every agent knows that every agent knows this proposition and every agent knows that every agent knows that every agent knows this
proposition, etc. ad infinitum, then it can be said that q is common knowledge: Cq.
Since ELPC is mainly concerned with the syntactic derivations of formulas and not with the semantics, I will not discuss the interpretation of formulas any further.
Interested readers are referred to wikipedia for a discussion on the semantics of epistemic formulas.
Epistemic Proofs
Deriving new facts in an epistemic proof system is a mechanical procedure.
A formal proof system consists of formulas which are either axioms or derived from other formulas using justification rules.
The axioms and justification rules that are used in ELPC are listed below.
Which axioms and justification rules can be used depend on the specific system that is used.
The problem of finding a proof for a formula is the hard part which is left for the user.
Checking whether the proof is correct is an easier task, which is done by ELPC.
Axioms and Rules
Different assumptions about the nature of knowledge lead to the next axioms and derivation rules.
Each axiom and each rule captures some property of knowledge.
The following rules and axioms are modelled in ELPC:
Axioms:
| A1: | (Instance of) Propositional Tautology |
| A2: | ⊢ (Kφ ∧ K(φ → ψ)) → Kψ |
| A2': | ⊢ K(φ → ψ) → (Kφ → Kψ) |
| A3: | ⊢ Kφ → φ |
| A4: | ⊢ Kφ → KKφ |
| A5: | ⊢ ¬Kφ → K¬Kφ |
| A6: | ⊢ Eφ ↔ (K1φ ∧ ... ∧ Kmφ) |
| A7: | ⊢ Cφ → φ |
| A8: | ⊢ Cφ → ECφ |
| A9: | ⊢ (Cφ ∧ C(φ → ψ)) → Cψ |
| A10: | ⊢ C(φ → Eφ) → (φ → Cφ) |
Rules:
| R1: | φ, φ → ψ | ⊢ | ψ |
| R2: | φ | ⊢ | Kφ |
| R3: | φ | ⊢ | Cφ |
Besides the aforementioned axioms and rules, there are some derived rules which can make proofs much easier.
Most of the rules are self evident, but all of them can be proved using abovementioned axioms and rules.
Derived Rules:
| KD: | φ → ψ | ⊢ | Kφ → Kψ |
| EI: | φ → ψ, ψ → φ | ⊢ | ψ ↔ φ |
| EE: | φ ↔ ψ | ⊢ | φ → ψ |
| EE: | φ ↔ ψ | ⊢ | ψ → φ |
| KD↔: | φ ↔ ψ | ⊢ | Kφ ↔ Kψ |
| HS: | φ → φ¹, ..., φⁿ → ψ | ⊢ | φ → ψ |
| HS↔: | φ ↔ φ¹, ..., φⁿ ↔ ψ | ⊢ | φ ↔ ψ |
| LR: | φ → ψ | ⊢ | (φ ∧ χ) → (ψ ∧ χ) |
| CP: | φ → ψ | ⊢ | ¬ψ → ¬φ |
| NC: | (φ ∧ ¬ψ) → ⊥ | ⊢ | φ → ψ |
| CO: | φ¹ → ψ¹, ..., φⁿ → ψⁿ | ⊢ | (φ¹ ∧ ... ∧ φⁿ) → (ψ¹ ∧ ... ∧ ψⁿ) |
| CO↔: | φ¹ ↔ ψ¹, ..., φⁿ ↔ ψⁿ | ⊢ | (φ¹ ∧ ... ∧ φⁿ) ↔ (ψ¹ ∧ ... ∧ ψⁿ) |
| SUB: | φ¹ ↔ φ² | ⊢ | ψ ↔ ψ[φ¹/φ²] |
Systems
Collections of different axioms and rules lead to different formal systems.
The abreviations for the axioms and rules are described in the section Axioms and Rules.
The systems that are modelled in ELPC are the following:
| Km: | A1 + A2 + R1 + R2 |
| Tm: | K + A3 |
| S4m: | T + A4 |
| S5m: | T + A5 |
| KECm: | K + A6 + A7 + A8 + A9 + A10 + R3 |
| TECm: | T + A6 + A7 + A8 + A9 + A10 + R3 |
| S4ECm: | S4 + A6 + A7 + A8 + A9 + A10 + R3 |
| S5ECm: | S5 + A6 + A7 + A8 + A9 + A10 + R3 |
Usage
To use ELPC, download the executable .jar file from the source code section.
Use the settings menu to select the proof-system of choice. Then select whether or not the derived rules are allowed to be used.
Every proof starts by entering the goal formula that needs to be proved.
Press ENTER after a formula has been entered.
Special characters can be entered by using the drop-down menu at the top of ELPC.
However, to make entering symbols easier, each symbol has a label that can be entered.
After pressing CTRL + SPACE all labels are converted to the corresponding symbol.
The list with symbol-names is as follows:
| label | symbol |
| true | ⊤ |
| false | ⊥ |
| not | ¬ |
| and | ∧ |
| or | ∨ |
| implies | → |
| equals | ↔ |
Besides this list, all Greek letters can be used as well by entering their Greek name without capital letters (see e.g. the list at wikipedia).
Therefore a formula like φ → ¬K¬φ can be inserted by typing: phi implies not K not phi CTRL + SPACE
After a formula has been added, choose a justification from the drop-down menu.
When a justification requires a reference line number, an input box is made visible where the relevant line numbers can be entered.
As soon as the goal formula is reached in the proof, the system will recognize this and indicate whether the proof is correct or not.
Example
In Figure 1 an example of a proof in S5m of φ → ¬K¬φ (using the derived rules) can be seen.
Figure 1
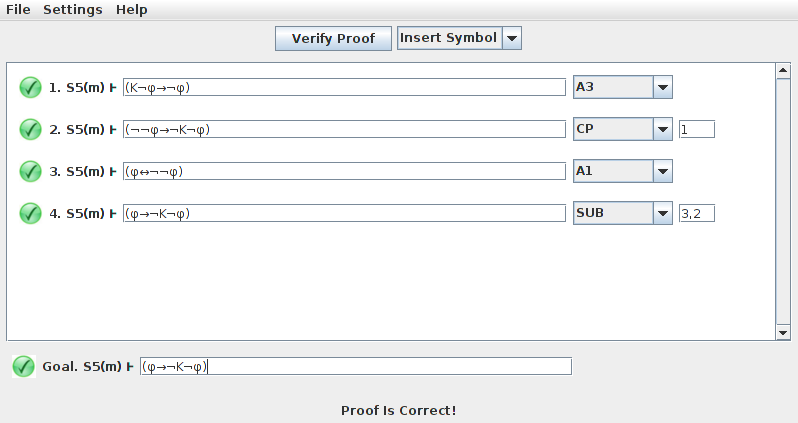 |
Other sample proofs are listed below. Save a file, and open it with ELPC (using the File/Open menu) to view.
EI
KD
LR
proof1_5_1_1_i
proof1_5_1_1_ii
proof1_5_1_2_i
proof1_5_1_2_ii
proof1_5_1_2_iii
proof1_5_1_2_iv
proof1_5_1_2_v
proof1_5_1_2_vi
Implementation
The code below is implemented in Java.
The most difficult part of the implementation is to check whether rule A1 is applied correctly.
Rule A1 states that every instantiation of a propositional tautology can be used as an axiom.
If the used formulas were strict propositional logic formulas, then verifying whether the formula is a tautology is straightforward: use a truth table to evaluate all valuations.
If all rows of the truth table evaluate to TRUE, then the formula is a tautology.
However, this principle cannot be applied with epistemic logic formulas, since the epistemic operators cannot be evaluated using truth tables.
For this reason the epistemic logic formulas are transformed to propositional logic formulas.
This transformation is done by cutting off the formula tree at all epistemic operators, and giving each cut a unique symbolic name.
For example the formula (p → q) ↔ (¬p ∨ q) is clearly a propositional tautology.
A possible instantiation could be: ((Kφ → Kψ) → K(φ → Kψ)) ↔ (¬(Kφ → Kψ) ∨ K(φ → Kψ)), with p = (Kφ → Kψ) and q = K(φ → Kψ).
The simplification is done as follows:
- At first all epistemic subformulas are collected. In this case they are [Kψ, Kφ, K(φ → Kψ)];
- For each formula in the collection: assign formula to a unique symbol: a = Kψ;
- Substitute the subformula in the original formula: ((Kφ → a) → K(φ → a)) ↔ (¬(Kφ → a) ∨ K(φ → a));
- Substitute the subformula in the collection of subformulas: [a, Kφ, K(φ → a)].
When this process is repeated for each subformula, the collection of subformulas is [a, b, K(φ → a)] and the simplified formula is ((b → a) → c) ↔ (¬(b → a) ∨ c).
Notice that this formula does not return to its original form, however this formula is a tautology if and only if the original formula is a tautology.
Also note how formula a is a subformula of formula c.
When the substitution [Kψ/a] is performed, this is not only done in the original formula, but also in the collection of subformulas.
So the final collection of subformulas is [a = Kψ, b = Kφ, c = K(φ → a)].
When the formula is simplified to a propositional formula, the tautologiness of the formula is checked using truth tables.
This is however a problem with exponential complexity in the number of atoms.
Source Code
Download Java executable (Start with java -jar ELPC.jar)
Download Source code Copyright © 2011 by Daniël Wedema
Created by Daniël Wedema for the multi-agent systems course in 2011

