|
Simulation and Recognition
of Handwriting Movements
A vertical approach to modeling human motor behavior
Proefschrift (PhD Thesis)
ter verkrijging van de graad van doctor
door
Lambertus Richardus Bernardus Schomaker
geboren 19 februari 1957 te Nijmegen
Promotores: ¯ Prof. Dr. A.J.W.M. Thomassen (psychologische funktieleer)
CIP-gegevens Koninklijke Bibliotheek, Den Haag Schomaker, Lambertus Richardus Bernardus Simulation and recognition of handwriting movements : a vertical approach to modeling human motor behavior / Lambertus Richardus Bernardus Schomaker. - Nijmegen : NICI, Nijmeegs Instituut voor Cognitie-onderzoek en Informatietechnologie. - Ill. Proefschrift Nijmegen. ISBN 90-9004044-7 geb. Trefw.: motoriek. Acknowledgement
Finally, I would like to thank my parents, and especially my wife Monica who was able to endure the peculiarities of a researcher's life, and who provided active support as well as the invaluable and fundamental conditions that are needed to perform this work.
Contents
Acknowledgement
Author Index Preface This study is concerned with the processes that take place from the moment that a writer wants to write down a given word, until he or she can inspect the finished result. What types of transformation are needed, going from planned word to muscle contraction? Which components of writing behavior are explicitly planned, and which components are emergent consequences of neural or biomechanical processes? The goal of this thesis is to enlighten at least to some extent these intriguing but hard-to-solve questions. The approach followed is based on the assumption that by trying to build a working generative computer model of handwriting, one will be confronted with the same types of problems that a human writer has to solve. As will become evident, this assumption is only partly true, since it merely holds for models that comprise more than a mere input/output description, and that try to reflect, at least partly, the internal architecture of the system under study. The starting point for the simulation model is the writing behavior of an adult writer, experienced in cursive writing. This implies that we disregard processes taking place during early motor development and during the learning of cursive handwriting. If we take a recording of writing movements during the production of a page of text by such an experienced writer, will it be possible then to analyze, transform and adapt these data to produce a completely new text, written in the cursive handwriting style of this subject? The aim of the present study is indeed to build a computer model that is able to generate handwriting patterns in such a way that there is a high correspondence with respect to both the spatial and the temporal characteristics between the handwriting production by the computer model and that by the human writer. The difference of this approach from most other attempts to model handwriting is that these latter models have tried to re-generate existing recordings of handwriting movements, mostly involving isolated words. As we shall see, the step from regeneration to new generation of movement patterns is far from easy. This thesis describes the research that evolved from the interaction between the demands of a working model, the experimental findings, and theoretical issues. Chapter 1 deals with the theoretical roots of the present endeavor. Many viewpoints reveal essential aspects of motor control, but no single viewpoint will suffice to provide the building blocks for a working model of handwriting production. Hence, a "vertical" approach is taken, adopting the necessary components for the different processing levels from cybernetics, cognitive motor theory, robotics and connectionism. Chapter 2 discusses an important aspect of the pen-tip kinematics during cursive writing: how reproducible are replications of writing movements recorded on different occasions? Only if movements are actually reproducible, makes it sense to develop a handwriting production model. This chapter forms the starting point of the development of the model, since it shows that invariance and replicatability are indeed present in movement patterns with the duration of at least a single letter. Chapter 3 presents a computer model of handwriting. One of the basic problems that have to be solved is concerned with the transformation of discrete entities, i.e., the symbolic representation of a planned letter shape (allograph), into a continuous multi-dimensional time function, i.e., the movement of the pen tip. This problem is tackled with the first step assumption that there are basic segments in handwriting, strokes, the number of which is known to have a more or less quantized influence on the reaction time in the programming of handwriting movements by a human writer. The next step is to find a parametrization of these strokes. Here, the problem is the fact that movements along more than one axis have to be prepared at a specific moment in time. In most models, the movement patterns along separate axes are essentially independent, describing the total pattern for an isolated word separately for each axis. In contrast, the current model aims at handwriting production that proceeds letter by letter. The reason for this constraint lies in the findings which seem to indicate that the motor programs used in planning cursive handwriting involve movement patterns of a size that corresponds to single letters. This assumption, consequently, leads to the definition of an abstract representation of allographs and a grammar, dubbed the Cursive Connections Grammar, that provides the rules for generating connecting strokes between two planned letters. Up to this point in the thesis, the model has only been concerned with the kinematics of the pen-tip movement. However, the important question may be asked if movement kinematics are the only domain that is controlled by the "programs" for handwriting production. Apart from the intrinsic forces that generate movement, the pen is in contact with the writing surface, yielding normal force and friction. What is the actual relation between finger and wrist movements and pen force (pressure)? If there is a fixed and strong relation between pen force fluctuation and movement, it is most parsimonious to consider pen force fluctuations to be a passive biomechanical phenomenon. If, on the contrary, pen force appears to be independent from the movement, it is likely to be a separate control variable. Thus, in Chapter 4, a kinetic aspect of writing is studied: what happens to axial pen force during the production of several types of movement patterns and what are the implications for movement control as specified in the working model? It appears that pen force fluctuations are not a passive biomechanical phenomenon. Also, the pen force pattern during letters is invariant across replications, which supports the notion that pen force is a separate domain, in some way embedded in the "programs" for letter production. During the course of our project, rapid new developments took place in the field of modeling perceptual and cognitive functions. New techniques in neural network simulations, such as back propagation, simulated annealing and neural self-organization are being refined and still newer techniques are being developed. With respect to motor control, however, there are still some typical problems to be solved, notably the representation of time and of continuous functions. Chapter 5 presents a review of some basic artificial neural network models and their potential use in modeling handwriting movement control. In the following chapters, three basic issues are raised with respect to motor modeling: the coding of quantity, the representation of time, and the representation of the effector system. Chapter 6 deals with the representation of quantity and learning the static transform of a continuous function. It reveals subtle differences between basic types of coding of quantity in a neural system: Firing rate control, value unit coding, and recruitment. In Chapter 7, the representation of time in neural systems and the learning of handwriting time functions is addressed. A new neural network model of the production of time functions is proposed, consisting of an ensemble of neuron-interneuron spike oscillators. The last of the three neural modeling experiments is described in Chapter 8 and concerns the problems of the representation of an effector (e.g., an arm) and the transform of two-dimensional movement patterns into N-dimensional joint angle patterns: The inverse kinematics problem. A final interesting and relevant problem is computer recognition of handwriting movements which is the focus of Chapter 9. Will the knowledge gathered thus far in simulating the production of cursive handwriting and in neural network modeling be helpful in the automatic recognition of handwriting movements? An algorithm is proposed that performs recognition by actively constructing letter (allograph) hypotheses on the basis of chains of individual strokes, instead of storing prototypical allographs and performing template matching.
Chapter 1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 1a. Typical reaction times.
|
Table 1b. Typical delay times.
As an approximate estimate, 100 ms is assumed to be the minimum time to
process sensory signals at cerebral
levels and initiate corrective muscle
contractions. Faster systems exist, e.g. the oculomotor system
(Gisbergen, Van Opstal, & Roebroek, 1987) with its short connections to the
central nervous system. However, the general opinion took hold
that the neural
system is just too slow to react fast enough to the rapid and often
sudden perceptual and
proprioceptive changes that occur in daily actions:
Car-driving, sporting and speaking, and to produce adaptive
corrective
activation of the muscles. The conclusion was that there process types must
exist which do not use feedback loops, but function, as it were, with an opened
loop. Thus, öpen-loop control" was acknowledged more and more as an
explanation for the timing problems in real-life motor control. Normally, in
cybernetics, open-loop control is an artificial situation, produced by an
experimenter to measure system parameters, such as gain, which can only be
determined if the feedback loops are cut. It is the engineer who determines
what the input signals are to the mutilated system, in order to measure the output
signals. In the case of motor control however, the notion of open-loop control
necessarily requires the introduction of a new concept. What type of signal or
information is flowing through this system with its feedback
loops inactive or ineffective? It must be some signal or ïnformation" that is
based on the current state of the perceptual systems and that
is anticipated to contribute to an adaptive state of the motor system by the
time the muscle contractions take place. The necessary concept is
"preparation" or "programming" as it is sometimes called. The term öpen-loop"
is also confusing since it presupposes that all existing
feedback loops are inactive, which is not the case.
Feedback loops varying from the mono-synaptic
reflex arc and the cortico-cerebellar loops
(Dimond, 1980) to the visual
feedback loop, are continually active, but the relevant
information is arriving "too late" in the case of rapid movements.
Apart from open-loop control by programming, there is a related but distinct principle that was postulated to explain the motor phenomena that appeared to operate without feedback: Feedforward control. The essence of feedforward control is, that earlier systems in a chain of processing units bypass the activity of intermediate processing units and bring about state changes in the units further away in the direction of the end of the chain. Feedforward control has the effect of overruling the activity of the intermediate processing units. In industrial engineering practice, feedforward is often used to implement safety mechanisms that prevent the system from overloading in case of input signals reaching ceiling values. The explanation that Dijkstra & Denier van der Gon (1973) put forward to account for the apparent ability of the motor system to reach a target after a disturbance without high-level feedback was the existence of a gamma-efferent feedforward signal that designated, a priori, the expected muscle length at the target location. This paper is typical for the transition from predominantly feedback-oriented explanations towards feedforward and ultimately, open-loop or programming-oriented explanations for phenomena in motor control.
The preliminary conclusion is, that cybernetics elegantly describes some existing phenomena in motor control. With respect to handwriting it can be concluded that the existence of feedback loops such as the mono-synaptic reflex arc and the cortico-cerebellar loops introduce a self-organizing autonomy into the effector system (the writing hand) in the domain of posture and stiffness control. At the same time however, the concept of feedback is insufficient to explain the corrective properties of motor control in case of absent or delayed sensory information. Also, the origin of complex patterns like writing is left implicit in a pure cybernetical theory.
2 The Open-Loop Approach: Cognitive Motor Theory
As stated earlier, the experiments by Bizzi (1980), Bizzi, Polit & Morasso (1976) played an essential role in the paradigmatic shift in which feedback as such was increasingly considered to be inadequate as an general explanation of motor control. It was shown that in fast aiming movements of the head or the arm (Wadman, 1979), final targets could be reached in the absence of essential feedback information (visual, vestibular, or proprioceptive feedback). The explanation for this phenomenon that was put forward, and that is still accepted for the greater part today, is that the central nervous system determines in advance of such an aiming movement, the ratios of muscle activation (co-contraction) levels. In this view, the motor apparatus is a combination of tunable mass-spring systems. The role of the existing feedback loops was consequently limited to (1) slow and fine adjustment as in posture control, to (2) adaptation to new or strange postures (Wadman et al., 1980), not internalized by the "programming" system, and (3) and to learning. These findings, as well as psychologically oriented models on motor preparation (Sternberg, Knoll, Monsell, & Wright, 1983) have influenced the development of a perspective we will call Cognitive Motor Theory. This field has exerted a marked influence, also on the development of theories on handwriting production (Hulstijn, & Van Galen, 1983; Hulstijn & Van Galen, 1988; Teulings et al., 1986; Van Galen, 1980). The paradigm has led to interesting discoveries that have been described extensively elsewhere (Teulings, 1988). However, there are some problems to the Cognitive Motor Theory. For example, the algorithmic view on motor processes inherently introduces discrete and sequential processing stages, and computer-based metaphors like "buffering" and ünpacking". In retrospect, an attractive aspect of cybernetics with respect to modeling motor control was that all the various processes function inherently parallel, in the models as well as in the neural reality. It is only recent that the concept of parallellism regains attention in staged and serial modeling (Van Galen, Meulenbroek, & Hylkema, 1986).
However, two basic aspects of the Cognitive Motor Theory approach are used and adhered to in the present thesis. The first is the concept of a motor program as a prepared system state that controls actual movement and that is of a more abstract nature than simple, stored muscle activation patterns. The second is the finding that "programming" is only possible for a motor action of limited duration. In other words, in order to be able to produce cursive handwriting, the motor control system must prepare the action in advance, but at the same time, it cannot prepare in detail more than a few of the basic movements (strokes) making up a specimen of handwriting.
A corollary of the open-loop approach is that the internal representations used in motor control can be used by the organism to process the (delayed) feedback information. Although the peripheral feedback information arrives too late to influence the individual stroke production, it can be used in the learning of handwriting (adjusting the "motor programs") and to compensate future strokes. As an example, deviations from the base line in handwriting can be compensated by adapting the vertical size of subsequent strokes. From a study in blindfolded writing (Schomaker & Van der Plaats, in prep.), it appeared that a striking difference between sighted and blindfolded writing lies in the reduced linearity of the base line.

Figure 2 shows two samples of handwriting of a single subject, in a normal (2a) and a blindfolded condition (2b). Apart from the non-horizontal orientation, the baseline is not linear because of within-word and between-word fluctuations. The between-word fluctuations are of a ßtaircase" type, caused by the positioning uncertainty at each pen lift. The positioning of the first word of a line of text was guided by the experimenter. It should be noted, that the mode of feedback that is involved here differs strongly from the physiological feedback in Section 1, in that it requires cognitive activity. The writer must see the handwriting base line or visually estimate it, in case of unruled paper, and he or she must know if the subsequent strokes have an end point that is located on the base line in order to produce an adapted "program" for the movements to come. The example also indicates that visual information is used to calibrate the global writing parameters size and orientation. In blindfolded writers, the orientation mostly deviates from the horizontal base line, but there are no systematic biases in the group of subjects. All 10 subjects wrote larger in the blindfolded condition. Apparently, the visual information is also needed for a feedforward Ëinstellung" of global parameters like orientation and size before the initiation of this motor task. The fact that writing size is systematically larger instead of smaller may be caused by the fact that larger movements compensate for the lack of visual feedback by larger muscle-length variations and a consequently enhanced proprioceptic feedback. Another effect caused by the removal of visual information is the so-called ßtroke counting error", here exemplified by the erroneous spelling of the words huis (house) and zee (sea) (Figure 2b, line 1 and 4 respectively) where a perseveration of strokes from the digram ui 2 or the letter e takes place. This effect has also been reported by others (Ellis, Young & Flude, 1987). This phenomenon points to the necessity of the visual detection of an ënd-of-allograph" condition, especially in the case of a repeating pattern.
3 The ecological viewpoint: The Systems Dynamics Approach
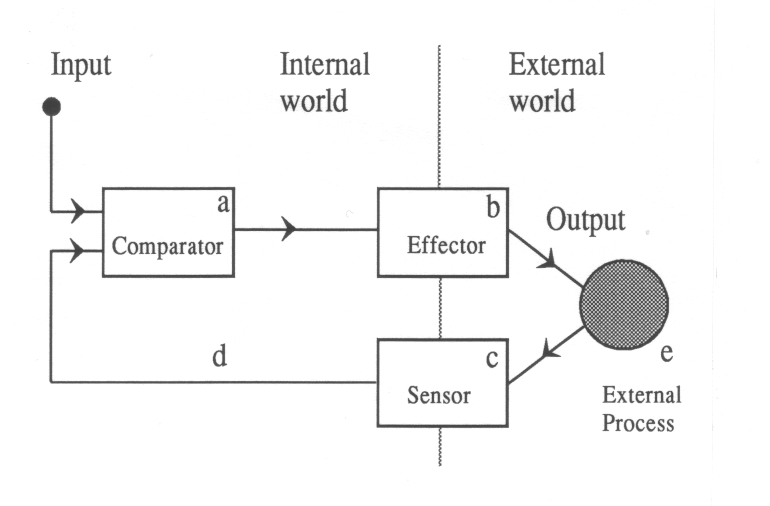
The ecological or "Gibsonian" perspective (Gibson, 1979) evolved from a growing discontent of several researchers who felt that the cognitivist, computational, approach complicated matters rather than explaining basic features of motor behavior and providing "deep" insight in these features. The cognitivist approach yielded complex models (Sanders, 1983), graphically depicted by connected "boxes", hence the term "boxology" (Bootsma, 1988). This type of model often appears to be somewhat remote from both the physical motor behavior and the physiological processes. More specifically, doubt can be cast whether all behavioral phenomena are explicitly programmed (computed). It is very well possible that motor control is brought about by a more autonomous process. In this latter approach, the idea of an internal representation of movement such as a stored pattern of receptor activity typical for a specific motor task is rejected.
Although the ecologists' criticism with respect to the cognitive approach is reviewed extensively elsewhere (Bootsma, 1988), it is useful to elaborate on some points. Interestingly, the ecological approach also partly rejects cybernetical explanations for motor behavior. For example, a given oscillatory component in a motor action pattern can be explained as the consequence of non-ideal servo behavior, but the same data can be described as being produced by a mass-spring system (Table 2), without the need for concepts like comparator, error correction and the like (Figure 1). In other words, in the eyes of the Gibsonians, a system may behave like some technical contraption, but it is considered more parsimonious to look at simple physical analogs for the description of the system as a whole. It is considered inappropriate to look for active system components if the data can be explained by passive mechanisms like attraction to equilibrium states. In a sense, the ecological perspective is holistic, not using concepts of physics in the regular reductionistical sense.
|
In many theories of the motor system the concept of mass-spring systems is
used. In fact, it is used so often that hearing the words will cause an
overhasty Äha Erlebnis" in many listeners. I would like to point out here,
that there are very large, sometimes subtle differences in the way the
mass-spring analog is used.
1. The mass-spring system as a direct analog for the
biomechanical behavior of the motor system.
2. The mass-spring system as an explanation for
feedback-less error adjustment.
3. Oscillations of a mass-spring system as a metaphor
for the organism-environment interaction. |
Table 2. The ubiquitous mass-spring analog.
In a paper by Saltzman & Kelso (1987), many basic concepts of the
Gibsonian
approach in motor theories are dealt with. These authors prefer to talk about
the "task-dynamic approach" when referring to their theory. However, the
term dynamic or dynamics is a frequent source of ambiguity (Table 3).
|
Often the terms dynamic and dynamics are used in a confusing way. There are at least three interpretations.
1. Dynamic as opposed to Static
2. Dynamic vs Kinematic
3. Dynamics as a method of analysis |
Table 3. The terms Dynamic and Dynamics and their meaning
In the sequel of this chapter, interpretations 2 and 3 (Table 3) will be
referred to using the terms Dynamics and System Dynamics,
respectively. In general, it would be profitable if the term kinetics
were used in case the force domain is referred to.
We will try to find arguments against the ecological approach and analyze two papers (Saltzman & Kelso, 1987; Beek & Beek, 1988) to see if the approach of Systems Dynamics is the ultimate panacea for the complexity problem in motor theories, and a good candidate for a handwriting production model.
1. It seems as if the differences in terminology between Cognitive Motor Theory and the Systems Dynamics Approach obscure the fact that it is the same motor system and the same motor processes that are the subject of study. This difference in terminology is maintained on purpose, carefully avoiding each other's concepts. In Saltzman & Kelso (1987), the term motor programming is carefully avoided, although the configuration of a Task network on the basis of Task space and Body space (ibid.) is clearly something like "preparation" or motor "programming".
2. There is a tendency to peruse anecdotal evidence. Example are the "diving gannet" (Lee & Reddish, 1981) and the ßkilled marksperson" (Tuller, Turvey & Fitch, 1982). There is no methodical, falsifiable approach in modeling as is used in some cognitive theories (Sanders, 1983).
3. The Systems Dynamics Approach virtually completely ignores the internals of the neural systems involved. In this sense it is purely descriptive. Only a very complex and matured device such as the human nervous system is capable of learning the task dynamics for a wide spectrum of motor tasks during an individual's lifetime, no matter how simple and parsimonious a dynamics description for the behavior in a specific task might be in terms of its mathematics.
4. The Systems Dynamics Approach is suited best for a limited class of motor tasks, i.e., oscillatory behavior, like walking which has since long been known to be produced by relatively independent and self-organizing low-level spinal and brain-stem modules. It can be fairly effective to describe other pure oscillatory tasks (Beek, 1989).
5. The parsimony of the Systems Dynamics Approach breaks down in complex patterning tasks. As an example we can take cursive handwriting. In this motor task, discrete action pattern units are concatenated. The model of Hollerbach (1981), assuming that the oscillator for a complete word is installed in advance does not hold. Writers only plan the movements for one or two letters ahead (Hulstijn & Van Galen, 1983; Stelmach & Teulings, 1983; Schomaker & Thomassen, 1986). Even if we would succeed in describing an oscillator configuration for a single letter, or even two letters, how then are the basic action units concatenated? Is this done by an associative process, or by "buffering"? Eventually, representational concepts will be needed, similar to those that are currently in use in Cognitive Motor Theory.
6. Looking at the Systems Dynamics Approach with a skeptical attitude, the method appears as an elaborate form of curve fitting, especially if one were to use it for modeling oscillatory behavior that is subtly modulated in phase, frequency and amplitude, like cursive handwriting movements. In this case the relation between the actual movement process and the original Newtonian equation of movement can be quite far-fetched, losing contact with the original physical parameters. The famous oscillator model of handwriting by Hollerbach (1981) needs 13 parameters. In a paper by Beek & Beek (1988), the phrase ßcouting for" (a non-linear function) can be found, conveying an essential problem of the approach that is characteristic of all curve fitting attempts. To understand the essence of this criticism, let us take a look at the method in more detail. Again, assuming the special case of cyclic tasks, an equation of motion can be given that describes a time-invariant periodic attractor:
| (1) |
Saltzman & Kelso (1987)
where m is mass, a is acceleration, b is the viscosity coefficient, v is velocity, k is the stiffness coefficient, s is displacement, and s0 is the equilibrium position. The non-linear escapement function f(s,v) is needed to counteract the energy loss caused by viscous friction. Given an appropriate f(s,v), the system described by this equation will tend to oscillate at a fixed frequency and a fixed amplitude, for all initial conditions of s and v, except for s = s0 Ùv = 0. The stable oscillating state occurs at the limit cycle in the system's phase portrait (v plotted vs s). A more realistic equation is given by Beek & Beek (1988), assuming that we cannot be certain that the friction (bv) is really viscous, or that the elasticity is linear and can be described by the term k(s-s0):
| (2) |
Beek & Beek (1988)
where W(s,v) comprises all deviations of the ideal mass-spring system in terms of friction and non-linear elasticity, including the escapement needed to keep the oscillation going. In other words W(s,v) is an extension of f(s,v). Note, however, that we are moving away from the idealized mass-spring system even further, and that the system described is a kinematic one, unlike equation (1). Given kinematic data, the goal now is to find a W(s,v) that is appropriate to model these data. Beek & Beek (1988) introduce several methods to decide if W(s,v) is one (combination) of a catalogue of non-linear functions (Duffing, Van de Pol, Rayleigh). What is the real purpose of searching after such an equation? A valid reason can be the fact that the domain described with the equation contains all temporal, spatial and/or force invariances (autonomously corrective effects) in a parsimonious way. But what if the complexity of W(s,v) exceeds other possible functional approximations to the term a + s? In other words, is the researcher allowed to fill in any non-linear function (polynomial, Fourier etc.) as long as the curve fits? It is essential that the Systems Dynamics Approach is adhered to as long as it describes motor phenomena in the most parsimonious way, keeping into account the physical and physiological limitations of the system under study. It appears however, that even in an evidently oscillatory task like juggling, other non-linear components like actively injected Dirac pulses have to be added to describe the behavior properly. Quoting:
In conclusion, all our evidence points to momentary action in the form of Dirac forcing pulses ('kicks') along the loop of the hand in addition to non-linear (and oscillatory, LS) behaviour. Hence the main tenets of the ecological approach are preserved, but dynamical research programmes, taking an a priori stand in favour of full autonomy and, thus not designed to reveal the presence of pulsed forcing, might well, through prejudice, miss the point.
And the point is, of course, that some active central nervous system process is involved in keeping the oscillation going, by intentional kicks (ibidem).
Looking at the modeling of cursive handwriting movements again, it can be reasoned that here a time-variant W(s,v,tk) would be needed for each temporal segment k coinciding with pieces of movement (letters or combinations of a very limited number of letters) that are produced by a corresponding non-linear oscillator. Most probably, just as in the juggling problem above, a time function of Dirac pulses has to be added if the influence determined by W(s,v,tk) is not sufficient to produce the trajectory. In both cases, parsimony is lost, leaving us with the usual non-autonomous patterning problem. This shortcoming of a pure äutonomous" approach makes it inappropriate as the sole basis for the development of a handwriting model. However, there are also several strong points in the Systems Dynamics Approach. We will discuss four of them.
1. Empirical findings indicating that a parsimonious
dynamical system
description is applicable to a specific motor task are intriguing. Indeed, a
repertoire of complex pattern generators or oscillators will lead to a
simplified mode of control. In terms of the Cognitive Motor Theory, the
specification of parameters for a general task program is simplified. But then
again, the non-linear dynamical system will
have to be configured or "geared
up" somehow, requiring active neural intervention on the part of the organism.
2. It is a misconception, indeed, that all kinematic phenomena must be planned explicitly. But apart from the Systems Dynamics Approach, also system-theoretical pulse-oriented models (Plamondon & Maarse, 1989; Dooijes, 1984) assume that the kinematic details are largely caused by the impulse response of the effector system.
3. The emphasis on the tight coupling between perception and movement does justice to the essence of behavior: The organism's goal is to survive in a chaotic and hostile environment. The study of perception and motor control in isolation would ultimately be detrimental to the development of cognitive science. The current approach in perception studies can be described as analyzing the facilities of a hypothetical philosopher who lives in a box and looks at the strange world outside through a hole. The study of motor control can be described as an attempt at analyzing hand and arm movements at a microscopic level while ignoring or forgetting about perceptual (visual, proprioceptive and tactile) processes.
4. The minimization of the assumed required cognitive (computational) resources needed for motor control is attractive. Many primitive species are able to produce incredibly complex movements, without possessing a cortex or cerebellum. From the ecological perspective, it can be argued that it is futile to try and model a single function in the behavior of an insect in terms of a cybernetical system, if there is only a limited number of receptors, ganglia and effectors available, each contributing to a number of functions at the same time. Equally, to model the behavior of such an insect in terms of a list of production rules (IF-THEN list) is only descriptive and too remote from the actual physiological system. It is one of the problems in cognitive science that elegance of modularity is preferred to such an extent that one tries to find modules everywhere. In fact, however, the pervasive idea of modularity in technology is something new, only becoming feasible when the cost per processing element (transistor) decreased to an acceptable level in the 1960's. Earlier, during the times of the radio tube (thermionic valve) it was considered excellent engineering practice to make optimal use of the dynamical behavior of the expensive tubes by combining as many functions as possible in a single tube, at the cost of losing the option of a clean and "maintenance-friendly" modularity. Since biological systems are self-maintaining, there is no external constraint necessitating the development of a degree of modularity which would be considered elegant by the scientist who tries to find order in a complex system.
4 Robotics
Robotics is currently a most stimulating technological field of interest to the researchers in psychomotor control. The compelling goal of building moving and manipulating flexible machines has led to the discovery of many new facts and to a clarification of previously underexposed concepts and implicit ideas. The following paragraph is an excerpt from a paper published earlier (Schomaker, 1988) 3.
Consider the mechanical structure of a biological or technical arm. An arm is composed of a series of inflexible oblong links, connected by joints. The joints can be classified according to the number of degrees of freedom (df) or movement axes, e.g., prismatic and revolute joints. As a simple two-dimensional example, let us take a piece of "meccano", consisting of four straight links. The first link is fastened to the table loosely with a screw, each other link is loosely connected to the end of its predecessor. We now have obtained an arm with four degrees of freedom. The next step is to draw a random scribble on the table. The purpose of this experiment is to consider how the free end of this mechanical arm, the hand, or end effector, can follow the scribble. Let us call the scribble the path that must be followed. Leading the "hand" along the path leads to irregular shapes of the arm. In fact, with this given arm, the path can be followed in an infinite number of ways: The time functions of the joint angles are indefinite. To impose some more constraints, we can identify points on the path and define the times at which the hand must be at the identified position. At this time we know the trajectory of the hand. Although the problem becomes tractable more and more, the time functions of the joint angles are still indefinite. Many different joint angle time functions are possible to obtain the same resulting trajectory. This is the essence of the inverse kinematics problem: How to calculate the individual joint angles in a complicated mechanical manipulator system if only the trajectory of the end effector is known? It is an example of a coordinate transformation problem from a 2- or 3-dimensional, Cartesian space, to an N-dimensional space of much higher dimensionality, and a typical ïll-posed" problem. To alleviate the problem, other constraints can be introduced, like a simple heuristic that states that changes in joint angle must be distributed evenly over all joints. Other constraints may consist of specifying the orientation of the end effector along the trajectory, apart from its end point. Nevertheless, there is no general computational solution to this transformation problem for all possible geometrical manipulator structures and numbers of df. On the other hand, humans solve the inverse kinematics problem continuously during movement, without being conscious of the computational effort involved. Only in the case of neurological disorders one becomes painfully aware of the complexity of the motor system (Schomaker, 1988).
In industrial robotics, the problem of inverse kinematics is approached by using numerical algorithms that are optimized with respect to computational speed (Luh & Lin, 1984; Paul, 1979; Hollerbach & Sahar, 1983). Still, these algorithms require a large amount of computation time, which increases steeply as the complexity of a robot arm, in terms of its number of df, increases. In practice, to simplify he computation, the geometrical structure of industrial robot arms is reduced to six df, of which three df are occupied by a spherical wrist.
|
A useful mathematical description of the inverse kinematics problem is
via the inversion of the Jacobian matrix J describing the current geometrical
state of a manipulator:
where dq is the vector of changes in the joint angles, J is the Jacobian, a function of the geometry of the manipulator and the current joint angles, and dX | df is a combined vector representing changes in the end effector position and angle with respect to the base. Problems arise in the case of a singular Jacobian and in the case of manipulators with a large number of degrees of freedom requiring a very large amount of computation (Desa & Roth, 1985). |
This restriction also reduces the use of high-level formal robot control languages, which cannot obtain their full potential in terms of flexibility in on-line control. Instead, in industrial practice, most of the trajectory formation is inflexible and taught to the robot by manual guiding: A human operator does the actual inverse kinematics computation for the robot system. And this introduces an intriguing question. How is the inverse kinematics problem solved in the human motor control system with its hundreds of degrees of freedom, its inherent non-orthogonal geometry and its complex relation between actuators (muscles) and joint angles? In handwriting, for example, one of the most complicated known manipulator systems is involved: The human hand. In chapter 8, we will consider solutions to the inverse kinematics problem.
However, there is more to motor control than end-effector trajectory formation and joint angle time functions. In an imaginary world without mass and forces the obtained joint angles are sufficient to produce a graphical computer simulation of the robot movements according to the planned trajectory. In the real world, on the contrary, objects, including the manipulator itself, are characterized by mass, stiffness and static and dynamic friction in case of contact with another object. This introduces forces which disturb the planned trajectory. There are also "parasitic" forces, like the Coriolis force resulting from the rotating links. The disturbances can only partly be counteracted by (post hoc) feedback (Section 1). This holds a forteriori for the biological motor control system with its limited force range (compared to gravitation) and its neural transmission delays. Consequently, it is necessary that the motor control system anticipates forces and torques. This introduces a problem, comparable to the inverse kinematics problem, viz., the inverse kinetics problem. What are the torques on the joints, given the size and orientation of a force applied at the end effector? This is not just a technical problem. As an example we take the experienced batsman in baseball. The available time for a hit is much too short to determine the necessary torque per joint during movement. Instead, he has to make use of an internal representation of the movement to plan the necessary torques and forces before the movement starts (Schmidt, 1982). This is especially important to maintain the body balance.
If a manipulator is in contact with an external object, the concept of compliance or mechanical impedance is needed. Objects may be damaged if the grip, push or pull force is to high. Therefore, controlled ëlasticity" is needed in a manipulator. In a motor system consisting of two antagonistic muscles around a 1-df joint (e.g., an elbow), compliance control can be achieved by lowering the activation levels for both muscles while leaving the ratio of their contraction levels constant. There exists a wide range of motor tasks, varying from opening a door to polishing a curved surface, where the requirement for a sophisticated control of compliance is evident. In handwriting, the movements of the pen-tip are confined to the two-dimensional plane, whereas the arm is a complicated 3-D object. One may expect that this has consequences for the pen force, e.g., the less compliance, the higher the pen force, if the pen-tip movement is not planned to take place exactly within the two-dimensional plane. Chapter 4 deals with the problem of the relation between pen-tip movement and pen force.
The robotics perspective broadly influenced the work in Chapters 3, 4 and 8, where the problems of inverse kinematics and inverse kinetics reappear.
5 The connectionist approach
There are some problems with the cognitivist approach to modeling motor control. The first problem concerns the symbolic character of the handwriting model that was developed (Chapter 3). Symbols are discrete and monolithic entities, whereas movement appears as a continuous process. Computing with symbols and computing with quantities are still separated fields in computer science, and it is not easy to find a symbolic formalism that does justice to the continuous nature of motor control. The proposed model (Chapter 3) provides an interface between the symbolic and quantitative domains. The second problem is of a more epistemological nature. Although a descriptive "Turing" approach to modeling can be very fruitful to gain insight in the computational aspects of motor control, there is a risk of deviating from the physical and physiological system to such an extent that the proposed computational stages are completely theoretical. Therefore, it seems necessary to take a step in the direction of model types that are closer to the intrinsic nature of the biological system performing motor control: The brain. The most intriguing feature of the brain is the fact that its single processing elements, the neurons, operate relatively slow (with firing rates mostly in the order of 100 Hz, maximally 1000 Hz), whereas the reaction time for a response in a large range of tasks of varying complexity is of an order of magnitude (150-1000ms). Given a fixed cortico-muscular delay, imposed by the axonal transmission and the muscle biomechanics, of 40-110 ms, it becomes apparent that the number of neurons involved in a perceptuo-motor task, counted as a single thread serially down the neuraxis, must be limited. Changes in activity are only updated at a pace of the inverse of the firing rate (intra-cortical transmission delays play a minor role since they are very short as compared to the delay in the efferent nerve trunk). As Ballard (1986) states: "...at the very least, this would seem to indicate that the cortex does massive amounts of parallel computation". The corollary of this observation is that the serial "loops", ïterations" and "recursion" in symbolic computational models of cognition are not likely to play a predominant role in neural activity, be it of a perceptual or motor control nature. It is far more likely that cognition is brought about by parallel computation of highly interconnected, but relatively slow processing elements. The field of research that is based on this insight is called "Connectionism". Its perspective raises new questions with respect to computation and representation in cognition and motor control, some of these are dealt with in Chapter 5. It is the purpose of the latter chapter to initiate the development of a complete neurally-oriented model of handwriting, the first steps being undertaken in the chapters 6 through 8.
6 Conclusion
In this chapter, a review of relevant theoretical viewpoints was presented. The eventual selection of ideas that are fruitful in the current modeling approach may be summarized as follows (the relevant sections within this chapter are shown in bold type).
Feedback systems provide a relative autonomy of the peripheral effector
system involved in handwriting, such that the central motor control system does
not have to specify all movement and force details (Cybernetics).
Feedback can be of a discontinuous, delayed nature, and still have an
effect on motor control (e.g., learning). This finding necessitates
representational concepts (Cybernetics and Cognitive Motor Theory).
Preparation and anticipation play a predominant role in handwriting, and
handwriting movement appears to consist of a stream of separable movement units
(Cognitive Motor Theory). The discrete character of handwriting movements
represents a good starting point for a symbolical model, which will be presented
in Chapter 3.
The transformation from perceptual and internal data to the effector domain
is a distinct and computationally non-trivial problem in all motor control
tasks, including handwriting. Also, the problems of force control and
compliance play an important role, which becomes evident if one imagines
what would be necessary to let a mechanical arm produce handwriting movements
(Robotics).
Although symbolical models of motor control may provide insight
on an abstract level, and display the idealized behavior of the
system under study, they may deviate substantially from what is realized in the
actual neural motor control system. In the symbolic
paradigm, symbols are objects that can be manipulated using the
appropriate formal operations. Such an object is representationally stable
(does not decay gradually) and can be operated upon an infinite number of
times. In the connectionist paradigm (Connectionism), a symbol is represented by a distributed
system state, which can be transformed by operations that are limited
by neural constraints. Here, the symbol (read: system state), is
representationally unstable, and of a transient nature, requiring an active
process such as selective attention or concentration. This essential feature
limits the number of ßymbols" that can be operated upon simultaneously, e.g.,
the well-known 7±2 limit (Broadbent, 1975), as well as
the number of operations that can be performed on them (how many people are
able to plan more than a handful of moves ahead in playing the game of chess?).
Consequently, a symbolic model is useful in describing some classes of
behavior, i.e., behavior that is based on transitions between discrete system
states, and that is performed under high mental concentration. Examples are the
neat production of connected cursive words without interjection of blockprint
allographs, the production of syntactically correct sentences, and the
evidently algorithmic processes like mental arithmetic. However, natural
behavior is characterized by errors that are indicative of the limitations of
the underlying cognitive processes (Harley, 1984). Also, in
motor behavior, such as handwriting, there are phenomena that are
incommensurable with a pure symbolic approach, such as quantitative pattern
transform, the production of smooth time functions and the representation of
the effector system. These functionalities in motor skills are non-symbolic
and difficult to express explicitly in linguistic terms. To describe this
observation, the concepts of "tacit knowledge" (Polanyi,
1967), and "behavior-based tasks" (Steels, 1989) have been
coined. In Chapter 3, this problem is partly solved assuming an interface
between the symbolic and the quantitative domain. In Chapters 5-8, however, the
perspective is switched to a more neurally-oriented viewpoint, in the hope that
new insights will emerge, especially with respect to the low-level aspects of
handwriting control that fall in the class of "tacit knowledge".
Finally, concurrent with the experiments on handwriting
production, work has been done in the field of pattern recognition. As a test
case for the theoretical insights on psychomotor control in handwriting,
Chapter 9 describes the problem of recognizing pen-tip movements in cursive
script, one of the goals of Esprit project 419 (Thomassen
et al., 1988). The practical problem of pattern recognition requires theories
and techniques that have been developed in the fields of electrical
engineering, statistics, artificial intelligence and computer science, rather
than in psychology. It is only with the introduction of connectionist models in
cognitive science (McClelland &
Rumelhart, 1986), that psychologists produced widely
accepted tools that really work for practical applications in pattern
recognition. Consequently, only part of the work presented in Chapter 9 and in
Teulings, Schomaker,
Gerritsen, Drexler, &
Albers (1990) will be of a "psychological" nature. However,
the psychomotorically inspired segmentation of handwriting movements in order
to describe movements in an abstract fashion (Teulings,
Thomassen, Schomaker &
Morasso, 1986), will prove to be very promising starting
point for ön-line" handwriting recognition. For the time being, we will revert
to the actual production of handwriting.
7 References
Author Index
Abraham, R.H., & Shaw, C.D. (1984). Dynamics, the geometry of behavior, part 1: Periodic behavior. (220 pages). Santa Cruz: Aerial.
Adams, J.A. (1971). A closed-loop theory of motor learning. Journal of Motor Behavior, 3, 111-149.
Allum, J.H.J, Dietz, V., & Freund, H.-J. (1978). Neuronal mechanisms underlying physiological tremor. Journal of Neurophysiology, 41, 557-571.
Ballard, D.H. (1986). Cortical connections and parallel processing: Structure and function. Behavioral and Brain Sciences, 9, 67-120.
Beek, P.J. (1989). Juggling dynamics. Doctoral dissertation. Amsterdam: Free University Press.
Beek, P.J., & Beek, W.J. (1988). Tools for constructing dynamical models of rhythmic movement. Human Movement Science, 7, 301-342.
Bendat, J.S., & Piersol, A.G. (1971). Random data: Analysis and measurement procedures, London: Wiley.
Bizzi, E., Polit, A., & Morasso, P. (1976). Mechanisms underlying achievement of final head position. Journal of Neurophysiology, 39, 435-444.
Bizzi, E. (1980). Central and peripheral mechanisms in motor control. In G.E. Stelmach & J. Requin (Eds.), Advances in psychology 1: Tutorials in motor behavior (pp. 131-143). Amsterdam: North Holland.
Bootsma, R.J. (1988). The timing of rapid interceptive actions. Doctoral dissertation, Amsterdam: Free University Press.
Broadbent, D.E. (1975). The magic number seven after fifteen years. In A. Kennedy & A. Wilkes (Eds.), Studies in long term memory (pp. 3-18). London: Wiley.
Crossman, E.R.F.W. (1960). The information capacity of the human motor system in pursuit tracking. Quarterly Journal of Experimental Psychology, 12, 1-16.
De Luca, C.J. (1979). Physiology and mathematics of myoelectric signals. IEEE Transactions on Biomedical Engineering, 26, 313-325.
Desa, S., & Roth, B. (1985). Mechanics: Kinematics and dynamics. In G. Beni & S. Hackwood (Eds.) Recent advances in robotics (pp. 71-130). New York: Wiley.
Dijkstra, S., & Denier van der Gon (1973). An analog computer study of fast, isolated movements. Kybernetik, 12, 102-110.
Dimond, S.J. (1980). Neuropsychology: A textbook of systems and psychological functions of the human brain. London: Butterworth.
Dooijes, E.H. (1984). Analysis of handwriting movements. Doctoral dissertation. Amsterdam: University of Amsterdam.
Ellis, A.W., Young, A.W., Flude, B.M. (1987). Afferent dysgraphia in a patient and in normal subjects. Cognitive Neuropsychology, 4, 465-486.
Fairbanks, G. (1955). Selective vocal effects of delayed auditory feedback. Journal of Speech and Hearing Disorders, 20, 333-346.
Gibson, J.J. (1979). The ecological approach to visual perception. London: Houghton-Mifflin.
Gisbergen, J.A.M., Van Opstal, A.J., & Roebroek, J.G.H. (1987). Stimulus-induced midflight modification of saccade trajectories. In J.K. O'Regan & A.Lévy-Schien (Eds.), Eye movements: From physiology to cognition (pp. 27-36). Amsterdam: Elsevier.
Grimby, L., Hannerz, J., & Hedman, B., (1979). Contraction time and voluntary discharge properties of individual short toe extensors in man. Journal of Physiology, 289, 191-201.
Harley, T.A. (1984). A critique of top-down independent levels models of speech production: Evidence from non-plan-internal speech errors. Cognitive Science, 8, 191-219.
Hogan, N. (1985). The mechanics of multi-joint posture and movement control. Biological Cybernetics, 52, 315-331.
Hollerbach, J.M. (1981). An oscillation theory of handwriting. Biological Cybernetics, 39, 139-156.
Hollerbach, J.M., & Sahar, G.S. (1983). Wrist-Partitioned Inverse Kinematic Accelerations and Manipulator Dynamics. MIT-AI Memo 717.
Hull, C.L. (1943). Principles of behavior: An introduction to behavior theory. New York: Appleton.
Hulstijn, W., & Van Galen, G.P. (1983). Programming in handwriting: Reaction time and movement time as a function of sequence length. Acta Psychologica, 54, 23-49.
Hulstijn, W., & Van Galen, G.P. (1988). Levels of motor programming in writing familiar and unfamiliar symbols. In A.M. Colley and J.R. Beech (Eds.), Cognition and action in skilled behaviour (pp. 65-85). Amsterdam: Elsevier Science Publishers.
Jones, R.W. (1972). Principles of biological regulation. London: Academic Press.
Kelso, J.A.S., Southard, D., & Goodman, D. (1979). On the nature of human interlimb coordination, Science, 203, 1029-1031.
Klir, G.J. (1969). An approach to general systems theory. New York: Van Nostrand Reinhold.
Laming, D.R.J. (1968). Information theory of choice-reaction times. London: Academic Press.
Lashley, K.S. (1951). The problem of serial order in behaviour. In L.A. Jeffress (Ed.), Cerebral mechanisms in behavior: The Hixon Symposium (pp. 122-130). New York: Wiley.
Lee, D.N., & Reddish, P.E. (1981). Plummeting gannets: A paradigm of ecological optics. Nature, 293, 293-294.
Lippold, O.C.J. (1970). Oscillation in the stretch reflex arc and the origin of the rhythmical, 8-12 c/s component of physiological tremor. Journal of Physiology, 206, 359-382.
Luh, J.Y.S., & Lin, C.S. (1984). Approximate joint trajectories for control of industrial robots along cartesian paths. IEEE Transactions on Systems, Man, and Cybernetics, 14, 444-450.
Marsden, C.D., Merton, P.A., & Morton, H.B. (1973). Latency measurements compatible with a cortical pathway for the stretch reflex in man. Journal of Physiology, 230,, 58-59.
McClelland, J.L., Rumelhart, D.E. (1986). Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Volume 1 Foundations. Cambridge, MA: MIT Press.
Morasso, P. (1981). Spatial control of arm movements. Experimental Brain Research, 42, 223-227.
Olson, P.L., & Sivak, M. (1986). Perception-response time to unexpected roadway hazard. Human Factors, 26, 91-96
Parker, T.S., & Chua, L.O. (1987). Chaos: A tutorial for engineers. Proceedings of the IEEE, 75, 982-1008.
Paul, R. (1979). Manipulator Carthesian Path Control. IEEE Transactions on Systems, Man, and Cybernetics., 9, 702-711.
Plamondon, R., & Maarse, F.J. (1989). An evaluation of motor models of handwriting. IEEE Transactions on Systems, Man and Cybernetics, 19, 1060-1072.
Polanyi, M. (1967). The tacit dimension. London: Routledge & Kegan.
Rack, P.M.H. (1981). Limitations of somatosensory feedback in control of posture and movement. In V.B. Brooks, (Ed.). Handbook of physiology, section 1: The nervous system, Vol. 2: Motor control, part 1 (pp. 229-256). Bethesda: American Physiological Society.
Redfearn, J.W.T. (1957). Frequency analysis of physiological and neurotic tremors. Journal of Neurology, Neurosurgery and Psychiatry, 20, 302-313.
Roberts, W.J., Rosenthal, N.P., & Terzuolo, C.A. (1971). A control model of stretch reflex. Journal of Neurophysiology, 34, 620-634.
Saltzman, E., & Kelso J.A.S. (1987). Skilled actions: A task-dynamic approach. Psychological Review, 94, 84-106.
Sanders, A.F. (1983). Towards a model of stress and human performance. Acta Psychologica, 53, 61-97.
Schmidt, E.M., & McIntosh, J.S. (1979). Excitation and inhibition of forearm muscles explored with microstimulation of primate motor cortex during a trained task. Abstracts of the 9th Annual Meeting of the Society for Neuroscience, Vol 5, pp. 386.
Schmidt, R.A. (1982). Motor control and learning: A behavioral emphasis. Champaign: Human Kinetics.
Schomaker, L.R.B., & Thomassen, A.J.W.M. (1986). On the use and limitations of averaging handwriting signals. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 225-238). Amsterdam: North-Holland.
Schomaker, L.R.B. (1988). Robotica en menselijke motoriek. In P.J.G. Keuss, G. Ten Hoopen & A.A.J. Mannaerts (Eds.), Psychonomische Publikaties: Menselijke Motoriek (117-140). Amsterdam: Swets en Zeitlinger.
Schomaker, L.R.B. & Van der Plaats (in prep.). Spatial and temporal effects on the writing of lines of cursive script by removing visual feedback.
Steels, L. (1989). Connectionist problem solving: An AI perspective. In R. Pfeifer, Z. Schreter, F. Fogelman-Soulié, L. Steels (Eds.), Connectionism in Perspective (pp. 215-228).
Stelmach, G.E. (1982). Motor control and motor learning: The closed-loop perspective. In J.A.S. Kelso (Ed.), Human Motor Behavior: An introduction (pp. 93-139). London: Erlbaum.
Stelmach, G.E., & Teulings, H.-L. (1983). Response characteristics of prepared and restructured handwriting. Acta Psychologica, 54, 51-67.
Sternberg, S., Knoll, R.L., Monsell, S., & Wright, C.E. (1983). Control of rapid action sequences in speech and typing. Approximate text of a speech held at the Annual Meeting of the American Psychological Association.
Teulings, H.L. (1988). Handwriting-Movement Control. Research into different levels of the motor system. Doctoral dissertation. Nijmegen University, The Netherlands.
Teulings, H.L., Mullins, P.A. & Stelmach, G.E. (1986). The elementary units of programming in handwriting. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 21-32). Amsterdam: North-Holland.
Teulings, H.L., Schomaker, L.R.B., Gerritsen, J., Drexler, H., & Albers, M. (1990). An on-line handwriting-recognition system based on unreliable modules. In R. Plamondon, & G. Leedham (Eds.), Computer Processing of Handwriting (pp. 167-185). Singapore: World Scientific.
Teulings, H.-L., Thomassen, A.J.W.M., Schomaker, L.R.B., & Morasso, P. (1986). Experimental protocol for cursive script acquisition: The use of motor information for the automatic recognition of cursive script. Report 3.1.2., ESPRIT project P419.
Thomassen, A.J.W.M., Teulings, H.-L., Schomaker, L.R.B., Morasso, P., & Kennedy, J. (1988). Towards the implementation of cursive-script understanding in an online handwriting-recognition system. In Commission of the European Communities: D.G. XIII (Ed.), ESPRIT '88: Putting the technology to use. Part 1 (pp. 628-639). Amsterdam: North-Holland.
Tuller, B.,Turvey, M.T., & Fitch, H.L. (1982). The Bernstein perspective: II The concept of muscle linkage or coordinative structure. In J.A.S. Kelso (Ed.), Human motor behavior: An introduction (pp. 253-270). London: Erlbaum.
Van Boxtel, A., & Schomaker, L.R.B. (1983). Motor unit firing rate during static contraction indicated by the surface EMG power spectrum. IEEE Transactions on Biomedical Engineering, 30, 601-609.
Van Galen, G.P. (1980). Storage and retrieval of handwriting patterns: A two stage model of complex behavior. In: G.E. Stelmach & J. Requin (Eds.), Tutorials in motor behavior (pp. 567-578). Amsterdam: North-Holland.
Van Galen, G.P., Meulenbroek, R.G.J., & Hylkema, H. (1986). On the simultaneous processing of words, letters and strokes in handwriting: Evidence for a mixed linear and parallel model. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 5-20). Amsterdam: North-Holland.
Von Hámos, L. (1964). Das Prinzip der Rückkopplung, der Regelung und der nichtdigitalen Rechenkomponenten. In H. Frank (Ed.) Kybernetische Machinen (pp. 133-150). Frankfurt: Fischer.
Wadman, W.J. (1979). Control mechanisms of fast goal-directed arm movements Doctoral dissertation. Utrecht University, The Netherlands.
Wadman, W.J., Boerhout, W., & Denier van der Gon, J.J. (1980). Responses of the arm movement control system to force impulses Journal of Human Movement Studies, 6, 280-302.
Wiener, N. (1948). Cybernetics: or control and communication in the animal and the machine. New York: Wiley.
Wurtz, R.H., & Mohler, C.W. (1976). Organization of monkey superior colliculus enhanced visual response of superficial layer cells. Journal of Neurophysiology, 39, 745-765.
Chapter 2
Planar pen-tip kinematics: invariance
The current chapter deals with a fundamental aspect in the modeling of handwriting behavior. Are handwriting movements replicatable at all, if a writer produces a given word several times? Only if there exists an invariance in the movement patterns over several replications, it becomes plausible to assume that handwriting movements are based on a stable internal representation that provides for the sequential launching of automatized movement units. Theoretically, the spatial shape of a given piece of handwriting trace on paper (the path) can be brought about by an infinite number of kinematic time functions (trajectories). Figure 0 shows several replications of a Dutch word, written with a vertical size of 2mm to 20mm, thus using a varying number of muscles in each replication. It is evident that there exists an invariance, both with respect to the shape and with respect to the pen-tip velocity pattern. The following experiment is a more detailed study concerning invariance in handwriting.
On the Use and Limitations of Averaging Handwriting Signals 4
Lambert R.B. Schomaker
Arnold J.W.M. Thomassen
Abstract
The averaging of handwriting signals is subject to a number of special restrictions that in general do not apply to other signals such as electrophysiological recordings. Specific problems are presented by the choice of the entities to be averaged, by the choice of time-reference points and by duration variability. Knowledge of the signal production mechanism and of temporal and spatial characteristics of the handwriting signal is needed to solve these questions. It is noted that the signal is deterministic at the local level, which justifies the use of averaging techniques. The problem of stroke duration variability is dealt with by applying time-axis normalization prior to averaging. Examples of averaging at the stroke, letter and word level are presented. Results indicate that at up to four letters can be averaged without noticeable distortion in the spatial domain. Eventually, however, variability in stroke duration will dictate the choice of time-reference points for the time-axis normalization in multi-letter handwriting segments. This will 'warp' the original time path. If care is taken in the selection of time references, time-axis normalization and averaging can be useful in movement analysis, pattern matching and simulation of handwriting.
1 Introduction
Ensemble averaging is a technique, used in many conditions where the reliability of measurement of a single sample record is reduced by some degree of noise. The measurement Xk may be assumed to be composed of a signal Sk and a noise component ek:
| (1) |
where ek is a stationary random signal and Sk is a fixed- duration transient with deterministic properties. The averaged signal [`X]k is obtained by:
| |||||||||||||||||||||||||
If the noise in the given samples is uncorrelated and the mean value of the noise is zero, then for large N:
| (4) |
Averaging of N sample records thus results in noise reduction: the variance of the error component of a single value k in [`X]k will be reduced with a factor 1/N (Bendat & Piersol, 1971; Regan, 1972). Apart from the random error, there may be a bias in each measurement, for instance caused by non-stationarities of the signal transient such as increasing or decreasing mean square value in the series of individual sample records. The main advantage of ensemble averaging over other methods of noise reduction such as low-pass filtering is that ensemble averaging selectively cancels noise contributions without affecting the 'true' signal portion of the spectral characteristics of the signal.
One major assumption in using averaging is the notion of time-lock. In many applications, the time reference used is an external event that triggers the occurrence of the transient to be measured. Furthermore, transients are assumed to have fixed duration. In practice, some jitter in the transient onset time and some variation in duration are taken for granted if they fall within predetermined limits. In handwriting signals, however, as well as in other types of free-floating human motor output, there are no external time-reference points and duration of segments having identical spatial representation may vary substantially. Nevertheless, it would be very useful in analysis, pattern matching and simulation of handwriting if an average representation of a specific stroke, letter or word produced by a certain writer were available to represent the idealized shape and dynamics of such handwriting segments for that person.
Therefore, we shall take a look into the main problems in selecting adequate time-reference points and in dealing with duration variability.
Before averaging of handwriting can take place, time-reference points have to be selected. From studies of handwriting it is known that the handwriting signal can be segmented reliably by taking the part of the displacement signal between two zero crossings in the Y-velocity signal as a stroke (Teulings & Thomassen, 1979). Another solution, taking the moment of maximum Y velocity as time reference is rejected because of its greater dependence on the velocity profile. Y strokes defined in the former way have the property of reflecting a combined agonist-antagonist muscle group action. Theoretically, the use of the acceleration signal would thus introduce the possibility of separating agonist and antagonist action. In practice, however, the double differentiation of the displacement signal leads to an unacceptable increase in noise level. The basic unit in averaging, therefore, will be a stroke in the velocity domain, the time-reference points being two adjacent zero crossings in the Y velocity. This also determines the time segment of the X velocity belonging to the same stroke. The velocity profile of Y strokes of a specific class (e.g. "last down stroke in a ") is very reproducible within a subject and varies from triangular to sine shaped. Velocity profiles of strokes that occur in a transition from clockwise to counter-clockwise movement are often bimodal or broadened, but their shape is reproducible for a given class (e.g., the connecting stroke from g to e ). According to the criteria by Bendat & Piersol (1971) we should classify single strokes as being deterministic transients (Note 1). Combined with the knowledge that zero crossings in the Y velocity are reliable time-reference points this justifies the use of averaging handwriting signals of a single subject at the local (i.e., stroke) level. It should be noted that, although single strokes can be considered to be deterministic, large segments of handwriting contain such a large amount of time and amplitude variations that they have to be classified as random time series. As a consequence, methods used for random data analysis like spectral analysis are still applicable on larger segments (minimally lasting five seconds) (cf. Maarse, Schomaker & Thomassen, 1986).
When a subject is asked to write a page of text, the movement duration of a specific letter will vary among the different realizations of that letter due to non-intended size and context effects. Thus, after selecting time-reference points, we shall have to normalize the time axis of the different replications before averaging. A comparable problem is encountered in speech recognition where the duration of the phonemes within a word may vary across several replications of the same word. If a minimum of assumptions with respect to signal shape is preferred and a fast computer is available, normalization of time axis can be done by means of Fourier transform (Note 2). A forward Fourier transform is done to obtain the amplitude and phase frequency spectrum, followed by an inverse Fourier transform with a time spacing of samples as determined by the ratio of old duration and normalized duration.
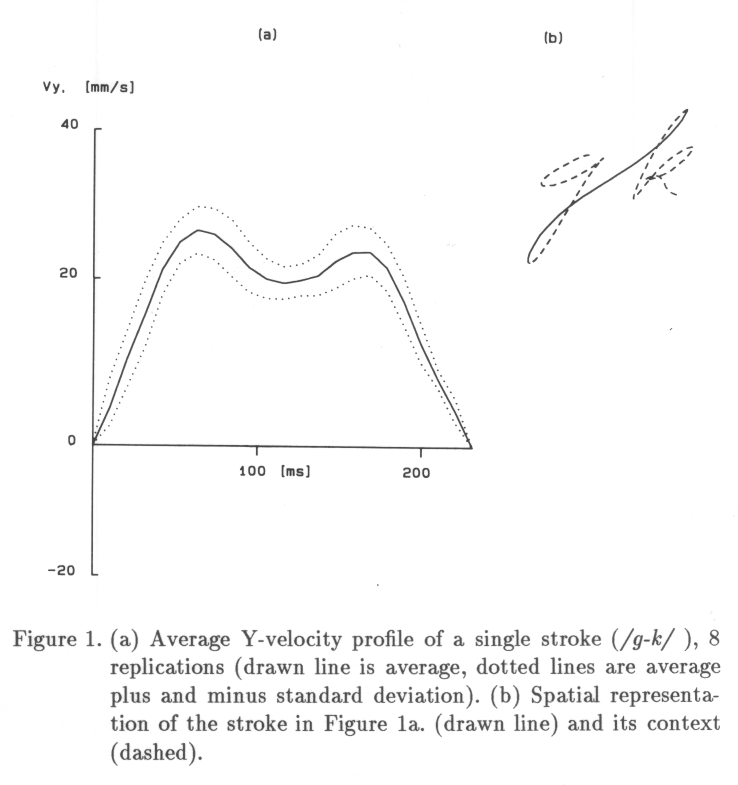
At the stroke level, an averaging technique may provide a reliable estimate of the strategy used to produce the displacement in that stroke. The velocity profile of a stroke determines the efficiency of its movement (Teulings, Thomassen & Van Galen, 1986). Figure 1 shows the typical (averaged) Y-velocity profile of a large up stroke in which a change of sense of rotation is produced. The stroke is the basic averaging unit. After time-axis normalization, the only sources of variability in a set of strokes are the stroke-size differences and differences in the shape of the velocity profile. Strokes may have equal size (area of the velocity profile) and have different shape of velocity profile.
Knowing that single strokes can be averaged, it would be interesting to know to what extent a given record of handwriting can be averaged. It is hypothesized that if the right time-reference points are chosen, sequences of strokes can be averaged also reliably if the movements are overlearned, e.g., in the case of a single letter , written by an experienced writer. The problem in averaging multiple-stroke handwriting segments is that each further stroke introduces a time variability, apart from the already mentioned size and shape variability. If the movements are overlearned, a handwriting segment can be assumed to be homothetic, i.e., ratios of stroke durations are constant in different realizations (Viviani & Terzuolo, 1980). Figure 2 shows the effect of the location of time reference for one letter. In 2a, it may be seen that the choice of Y-velocity maxima in connecting strokes leads to an unacceptable distortion of the average letter representation in the spatial domain. Cause of the distortion is the fact that connecting strokes are embedded in the motor context of the end of the previous letter and the start of the next letter. A better choice may be seen in 2b, where the first and last zero crossings of the Y-velocity signal within the letter proper were used as time-reference points, disregarding the connecting strokes.

In the case of naturally produced handwriting, the
straightforward averaging of even larger units, such as
words , is made increasingly more difficult by hesitations,
pen-up
movements and allograph variations that may be expected to
disturb the homothetic features of the movement sequence.
Also, in these larger
units, there is an increased probability of non-overlearned
sequences to
introduce a greater time variability. For instance,
connecting strokes may or may not be part of a motor program,
depending on the degree of automation of the specific sequence
of letters.
In sequences encompassing instances of evidently large
time variability due to occasional hesitations or pen-up
movements, a time warping technique might be necessary, i.e.,
segmenting the handwriting into pieces each of which can
be assumed to be homothetic, and
normalizing time for each
segment separately. Once this has been done, ensemble averaging
or pattern matching can be applied. In speech recognition, this
problem is solved, using an optimal time-alignment procedure
called dynamic time warping
(Brown & Rabiner, 1982).
From an exceptionally regularly writing subject the average word computer could be obtained (Figure 3a), but hesitations and prolonged stroke duration may cause distortions (Figure 3b) if they are not accounted for in the averaging procedure. The average word gen is distorted by a hesitation before executing the down stroke in g in the last of the five replications (the hesitation cannot be inferred from the spatial representation).

In order to assess the discussed problems encountered in averaging multi-letter segments of handwriting in greater detail, we shall analyze some experimental data in the next sections of the present paper, using time-normalization and averaging techniques. The following aspects will be illustrated.
Deviations from the average Y-velocity pattern can be attributed to time, size and shape variations (note that in the current study stroke size is not normalized in any way). Possibly large deviations from the average pattern are indicative of transitions between discrete states in the motor production process. Such transitions are likely to occur during movements connecting one letter to the next. Consequently, three types of connecting strokes will be examined.
If we know the average stroke duration of each stroke, the uncertainty of finding the stroke ending of the n-th stroke in some time segment in the velocity signal increases with the number of strokes since each new stroke adds its variability in duration. Normalizing the time axis will have the effect of reducing this uncertainty in a curvilinear fashion, maximum uncertainty remaining around the middle of the handwriting time segment. In the limiting case where the variance of stroke duration is the same for all strokes, the variance of stroke onset time will be proportional to stroke number (first stroke is number zero) before normalization. After normalizing the time axis, the variance of stroke onset time will be proportional to n * (N - n), where n is the stroke number and N is total number of strokes.
2 Methods
Two adult right-handed male subjects, aged 49 and 28, participated in the experiment.The movements of the tip of the writing stylus were recorded by means of a large-size writing tablet (Calcomp 9000) connected to a computer (PDP 11/45). The laboratory-made writing stylus was equipped with a pressure transducer. The stylus contained a normal ball-point refill. Thirty-eight pseudowords were printed on specially prepared A4 response sheets in twelve rows of two to five words each. A row contained a certain 'family' of pseudowords allowing specific comparisons. The rows themselves were placed in a quasi-random order. Pseudowords contained minimally three letters, the maximum was five letters. From this material, the pseudowords , and are selected for the present purpose since they contain an identical part (ag) and a contrasting part, that starts with three possible types of large connecting strokes, i.e., g-u which ends in a sharp cusp, g-n which ends in clockwise turn, and g-e which consists of a clockwise and a counter-clockwise turn in one stroke.
The subjects' task was to write on the response sheet immediately below the place where the pseudowords were printed. The response sheet was placed on the writing tablet and was held by the subject in a convenient position and at a preferred angle, just as in a normal writing situation. A pseudoword had to be written fluently without raising the pen. A session consisted of writing the 38 pseudowords on the sheet once. An experimenter-controlled tone sounded to signal the onset of a 2.5 s period during which the writing could be produced. Two tones signalled the end of the interval. All pseudowords could easily be written within this 2.5 s period, so that no time pressure was imposed on the subject. The experimenter took care that he did not start the interval until the subject's hand rested at approximately the appropriate position for the next word. If the subject was not satisfied, due to hesitations, errors (e.g. selection of incorrect allographs), jerks, late starts or slow movements, he was immediately given another trial in which the word was written below the rejected product. A session, which lasted only four minutes, could be followed by a further session after a rest of a few minutes, or sessions could be separated by a whole day. Each subject completed ten sessions.
The X and Y-coordinate values and the pressure at the tip of the pen (Z coordinate) were sampled during 2.5 s intervals at a 105 Hz rate, samples having an accuracy of 0.02 mm in both X and Y directions. Prior to our analyses, these handwriting data were digitally filtered with a finite-impulse response filter (pass band 0 to 10 Hz, transition band 10 to 30 Hz; Rabiner & Gold, 1975). Since the orientation of the handwriting was left to the writer's preference data were automatically rotated to obtain a horizontal baseline, using the low extremes of small letters as a reference. Velocity signals were calculated by differentiating the handwriting coordinates versus time using a five-point finite-differences impulse response (Dooijes, 1984). Handwriting was segmented on the basis of zero crossings in the Y-velocity signal, the first point in a segment being the start of the first down stroke in the first letter (a ), the last point being the end of the last stroke of the last letter (e) in the analyzed pseudowords. Of each word (ague, agne and agee) eight replications per subject were entered in the analysis. The average duration of each word was used as the reference duration in the time-axis normalization. After time normalization, the average Y-velocity pattern and its standard deviation (SD) pattern were calculated (N=8) for each word and each subject separately. For comparison purposes and data reduction, the following measures were calculated per Y stroke. From the time-normalized replications, SD of stroke size and SD of stroke duration were determined. From the average Y-velocity and the individual time-normalized Y-velocity replications, the SD of the average Y-velocity pattern was calculated. The latter measure was obtained by pooling sums of squared deviations per stroke.
3 Results
The mean word durations are shown in Table 1. Of the ten sessions, two sessions were lost due to technical problems.
| Word | Subject 1 | Subject 2 | ||||||
| mT | sT | mn | Nw | mT | sT | mn | Nw | |
| [ms] | [ms] | [samples] | [words] | [ms] | [ms] | [samples] | [words] | |
| ague | 1467 | 68 | 154 | 8 | 1457 | 100 | 153 | 8 |
| agne | 1419 | 52 | 149 | 8 | 1423 | 80 | 150 | 8 |
| agee | 1305 | 41 | 137 | 8 | 1257 | 102 | 132 | 8 |
Figure 5 shows the variability in time of zero crossing, before and after time-axis normalization. Note the overall decrease in variability and the curvilinear relationship between stroke number and stroke-onset time variability after normalization.
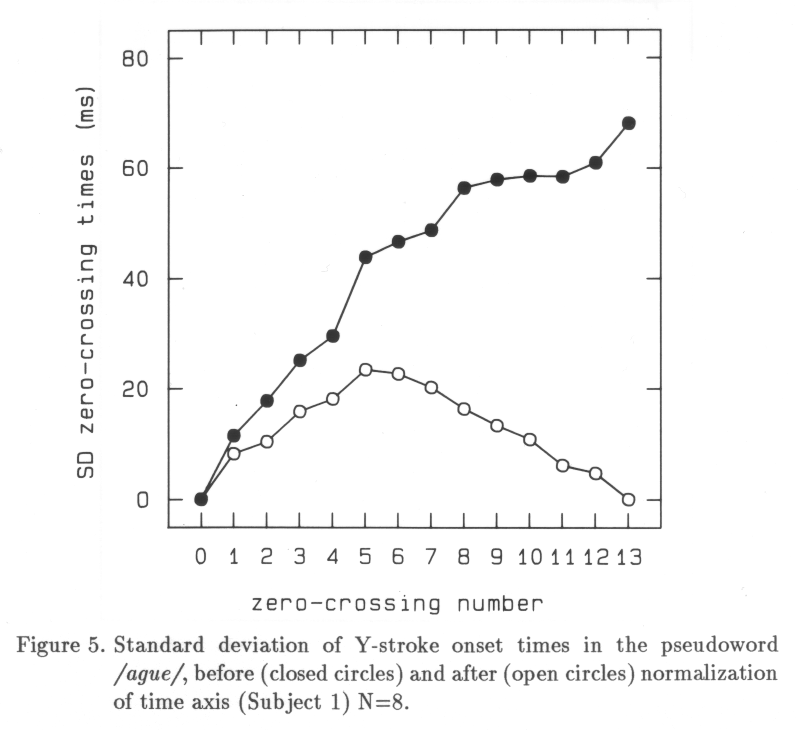
Figures 6, 7 and 8 allow a comparison of three types of variability per stroke. The a_panels show the deviation from the average Y-velocity pattern. At the seventh stroke, which is the large down stroke in , there is a peak in the variability of the Y-velocity. This peak is not related to the curvilinear stroke-onset variability caused by time normalization, because it occurs in the same place for the 13-stroke words ague and agne as for the 11-stroke word agee. Shifting the first time-reference point up to three strokes to the right, moreover, had no influence on this effect: variability always remained maximal at the large down stroke in (not shown). The largest variability (peak as well as overall) is reached in , followed by , and finally if both subjects are combined. The b_panels show stroke size variability. There is no clear peak at the seventh stroke. In fact, a peak occurs at the eighth stroke which is the connecting stroke . Only in Figure 8 () stroke size variability is also high at the seventh stroke as written by Subject 1. The c_panels show stroke-duration variability which is increased at or around connecting strokes (numbers 4, 8, 12). There is no clear relationship between duration variability and the variability in Y-velocity at the seventh stroke itself.
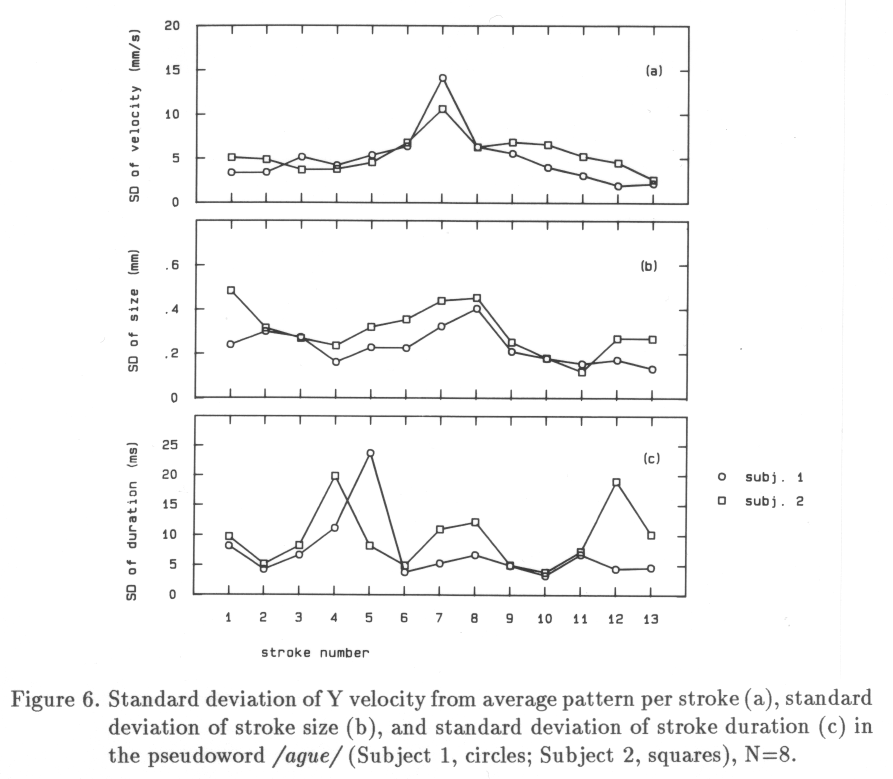
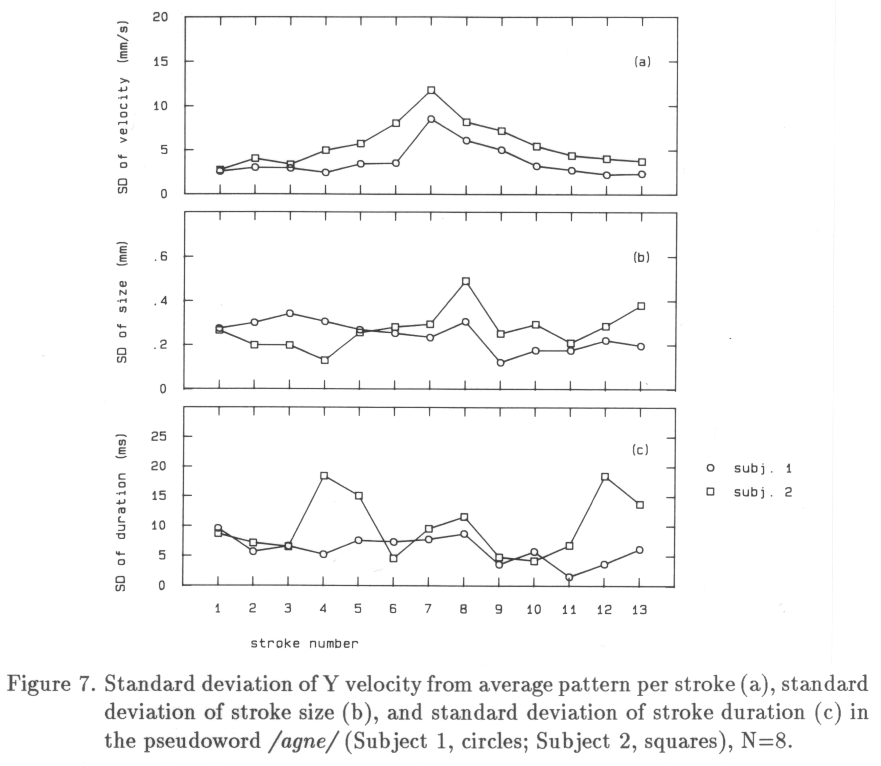
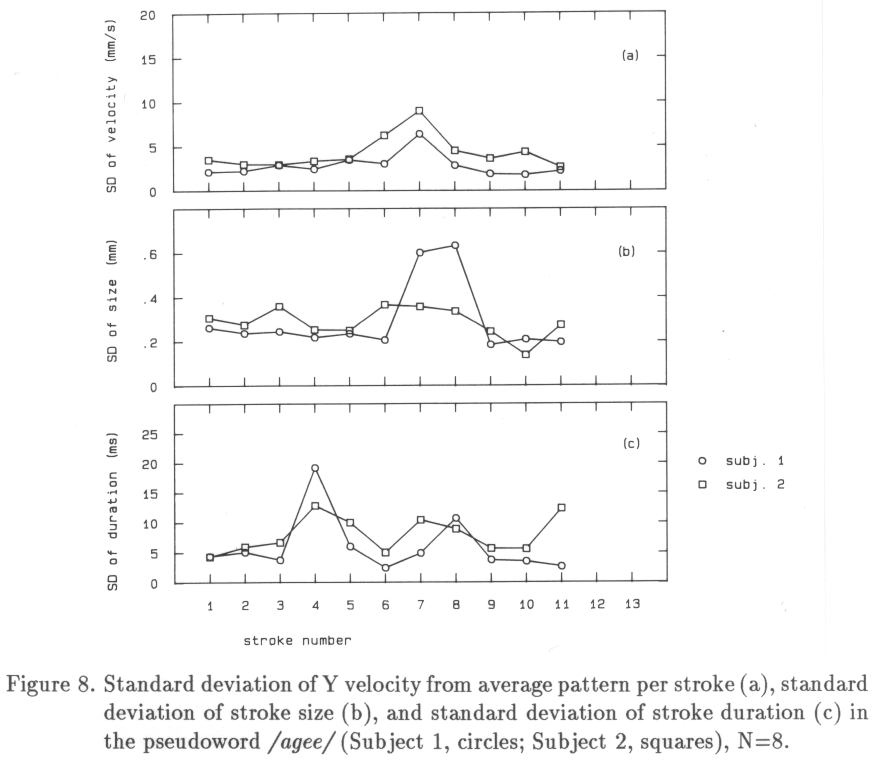
4 Discussion
An interesting finding of the present study is that handwriting segments up to four-letters can be averaged very well because the consistency across the individual replications is high, even though the task involved pseudowords. Normalization of the time axis was a sufficient condition to obtain a reliable average. Within a subject, normalizing stroke size seems to be unnecessary. The detected peak deviation in the Y-velocity remains a problem to be explained. The possibility of an artefact caused by the normalization operation may be excluded since the effect was independent of number of strokes or time reference chosen. Size and duration variability of the stroke itself are unlikely to cause the effect (Figures 6, 7 and 8). Another source of error could be variable shape of the velocity profile of the large down stroke in . Inspection of Y-velocity profiles of the individual replications indicated that this was not the case. In fact, the source of the effect can be traced back to the occurrence of duration variability earlier in the pattern, at the fourth and fifth stroke. Possibly this variability can be explained by anticipation of the large down stroke in and the subsequent large connecting stroke. In this case, the duration variability did not cause visible distortion in the spatial representation of the average. It is advisable, however, to analyze the variability of stroke onset times (Figure 5, closed circles) before time-axis normalization. At the location of sudden increases in variability the handwriting signal should be split up in subsegments. To obtain a more reliable estimate in the case of the pseudoword ), subsegments would be: (a) strokes 1 to 4; (b) stroke 5; and (c) strokes 6 to 13.
The time normalization technique can be a valuable tool in movement analysis, pattern matching and simulation. Before it can be applied, however, careful inspection of the of the stroke-onset time variability appears to be needed. When the homothetic assumption is violated in a handwriting segment, subsegments have to be defined, thereby 'warping' the time axis. In movement analysis, time normalization and averaging can be used to detect special strategies in the velocity profiles that are used by the subject to obtain specific curvature shape in the spatial domain. In pattern matching of handwriting signals the technique can be of use by providing reliable averages that are used as templates. In the matching process itself, time normalization is used to enable matching of a specific handwriting pattern with the template. In simulation of handwriting, time-axis normalization is used to obtain reliable averages of letters and connecting strokes from a writer. Only reliable averages allow the determination of important parameters in the simulation model.
Use of the Fourier transform has the disadvantage of being time consuming. Fast Fourier has the disadvantage of requiring sample record sizes that are powers of two (the technique of adding zeros appeared to cause unacceptable distortion). The use of splines is rejected because it also can introduce serious estimation errors. During the last few years, much work has been done on this subject. Methods of interpolation using finite impulse response differentiation are promising with respect to calculation time (Sudhakar, Agarwal & Suhash, 1982).
5 Appendix
- If an experiment producing specific data can be repeated
many times with identical results, within the limits of
experimental error, then the data can be considered
deterministic. If such an experiment cannot be designed, then
the data are considered random (Bendat & Piersol, 1971).
- The steps necessary to achieve time-axis normalization using
Fourier transform are as follows:
- Determine normalized duration Tn and normalized number of
samples Nn by averaging movement duration of the different
replications.
- Calculate x and y velocities.
For x and y:
repeat steps (c) to (g) for each sample record with Ni values. - Make sample record circular by
linear detrending.
- Apply forward Fourier transform with Ni frequency domain
estimators, with k = 0 to Ni-1.
Xk = Ni-1
å
n = 0(xn e-j pkn/Ni) (5) - Apply inverse Fourier transform with Nn time domain
estimators, with n = 0 to Nn-1.
xn¢ = Ni-1
å
k = 0(Xk e+j pnk/Nn) (6) - Decircularize sample record by restoring linear trend.
- Gain correction (multiply sample record with Ni/Nn).
- Determine normalized duration Tn and normalized number of
samples Nn by averaging movement duration of the different
replications.
6 References
Bendat, J.S., & Piersol, A.G. (1971). Random data: Analysis and measurement procedures (pp. 1-55). London: Wiley.
Brown, M.K., & Rabiner, L.R. (1982). An adaptive, ordered, graph search technique for dynamic time warping for isolated word recognition. IEEE Trans. on Acoustics, Speech and Signal Processing, 30, 535-544.
Dooijes, E.H. (1984). Analysis of handwriting movements. Doctoral dissertation. Amsterdam: University of Amsterdam.
Maarse, F.J., Schomaker, L.R.B., & Thomassen, A.J.W.M. (1986). The influence of changes in the effector coordinate system on handwriting movements. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 33-46). Amsterdam: North Holland.
Rabiner, L.R., & Gold, B. (1975). Theory and application of digital signal processing. Englewood Cliffs, NJ: Prentice-Hall.
Regan, D. (1972). Evoked potentials in psychology, sensory physiology and clinical medicine (pp. 243-248). London: Chapman and Hall.
Sudhakar, R., Agarwal, R.C., & Suhash, C.D.R (1982). Time domain interpolators using differentiators. IEEE Trans. on Acoustics, Speech and Signal Processing, 30, 993,997.
Teulings, H-L., & Thomassen, A.J.W.M. (1979). Computer aided analysis of handwriting. Visible Language, 13, 218-231.
Teulings, H.L., Thomassen, A.J.W.M., & Van Galen, G.P. (1986). Invariants in handwriting: The information contained in a motor program. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary Research in Handwriting pp. 305-315. Amsterdam: Elsevier.
Viviani, P., & Terzuolo, V. (1980). Space-time invariance in learned motor skills. In G.E. Stelmach & J. Requin (Eds.), Tutorials in motor behavior (pp. 525-533). Amsterdam: North Holland.
Chapter 3
A computational model
After having collected data on the replicatability of movement patterns, an experiment was done to assess the influence of surrounding characters, i.e., the temporal context on the size and duration of strokes in handwriting (Thomassen & Schomaker, 1986). From the experiment it appeared that temporal context influences are present, displaying most of their effect in the temporal domain (stroke duration). As an example: in writing the cursive word , the duration of the down strokes of the 's is different, the first being written faster. At the same time, however, the effects seem to differ in magnitude and direction between subjects, such that a general "law" could not be determined easily. It was decided to continue the development of the handwriting model without incorporating these subtle context effects until more is known about their origin.
So, a computer model was developed that represents the computational stages in transforming discrete letter identities into continuous movement. The transform is from a symbolical representation at the "higher", cognitive, level into a quantitative representation at the "lower", spatio-temporal motor level. An essential aspect of the model at the lower non-symbolical level is a representation of spatial stroke shape that is based on differential relative timing. Indeed, it is the relative timing of muscular contractions: the subtle switching On and Off of muscle groups during a complex action, that determines the spatial characteristics of the resulting movement path. It is shown that shape, as expressed in the end-point curvature, can be defined in terms of the relative difference in timing of two orthogonal effector sub-systems, with the overall movement duration as the local reference. In earlier theories, the concept of phase shift was used (Hollerbach, 1981), assuming that there is a single (narrow-banded) fundamental frequency of a two-dimensional phasor signal generated by a mass-spring oscillator, that determines the shape of the handwriting. The weakness of this assumption becomes clear if one examines the frequency spectrum of handwriting movements (Teulings & Maarse, 1984; Maarse et al., 1986) or the distribution of stroke size and duration in handwriting. The changes in the movement parameters are occurring on a stroke-to-stroke basis. The existence of this subtle concatenation of events reduces the likelihood of an oscillator mechanism as the central explanation for the production of words in handwriting, as evidenced by the large number of parameters needed to describe word production in terms of a mass-spring oscillator. In this chapter, the alternative view is taken, i.e., that there exists an active pattern generator mechanism, leading to movement behavior that may appear oscillatory at times, within a limited time window, but that is basically a fluent concatenation of discrete and limited-duration movement segments with a temporal range of typically a single letter.
References
Hollerbach JM (1981). An oscillation theory of handwriting Biological Cybernetics, 39, 139-156.
Maarse, F.J., Schomaker, L.R.B., & Thomassen, A.J.W.M. (1986). The influence of changes in the effector coordinate systems on handwriting movements. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 33-46). Amsterdam: North-Holland.
Teulings, H.L., & Maarse, F.J. (1984). Digital recording and processing of handwriting movements. Human Movement Science, 3, 193-217.
Thomassen, A.J.W.M. & Schomaker, L.R.B. (1986). Between-letter context effects in handwriting trajectories. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 253-272). Amsterdam: North-Holland.
A computational model of cursive handwriting. 5
Lambert R.B. Schomaker
Arnold J.W.M. Thomassen
H.L. Teulings
Abstract
This paper presents a computational model for the production of handwriting, starting with allograph codes as input and ending with a target pen-tip trajectory as output. In the model, a distinction is made between a symbolic level of processing and a quantitative level of processing. At the symbolic level, a grammar for the connection of cursive allographs determines abstract codes for connecting strokes. At the quantitative level, a translation of symbols into a sequence of parameterized strokes takes place. A parsimonious stroke parameterization in the velocity domain is used, that is based on planning in Cartesian space and allocation of time to movement components along the spatial axes. With the basic model settings used, simulation results already show a satisfactory correspondence with original handwriting samples.
1 Introduction
Attempts to generate new cursive script by means of a computer confronts us with the fundamental problems that the human motor system has to solve likewise. In the past, many models of handwriting were proposed, basically aiming at digital or analog regeneration of existing samples of handwriting (Denier van der Gon et al., 1962; Vredenbregt & Koster, 1971; Hollerbach, 1981; Dooijes, 1984; Plamondon & Lamarche, 1986; Maarse, 1987). This paper discusses a computational model that describes the generation of new samples of handwriting on the basis of motor principles and on the basis of knowledge of idiosyncratic features of the handwriting of a given individual.
The production of handwriting requires a hierarchically organized flow of information through various transformations (Ellis, 1986; Teulings et al., 1987). The writer starts with the intention to write a message (semantic level), which is transformed into words (lexical and syntactical level). When the individual letters (graphemes) are known, the writer selects specific letter shape variants (allographs). This selection is done according to a formal allograph selection syntax, according to individual preferences or just according to random choice. A formal rule, for instance, is the use of a capital letter at the beginning of a new sentence. An example of preferential context rules is the use of differently shaped versions of or , depending on the adjacent allographs or on the serial position of these letters in a word.
Below this level we enter the scope of the current model, were the allographs are transformed into movement patterns. Both spatial and temporal characteristics of error-free, non-hesitant handwriting tend to show some invariance for a given writer. However, it has been shown that there exists a tendency for the spatial characteristics to be more invariant than the temporal characteristics (Teulings et al., 1986). The reason for this can possibly be located in the nature of handwriting as a means of linguistic communication. It seems reasonable to assume that the handwriting production system 'stores' the information pertaining to the task-related constraints: the produced spatial shapes are to be read by someone at a later time. Also, the spatial characteristics of handwriting are strongly consistent for a given writer (Maarse et al., 1986), regardless of the end effector or writing apparatus used (Raibert, 1977). Therefore, we assume that there exist spatial representations of allographs, residing in some long-term memory. These idiosyncratic spatial allograph representations (paths) have to be transformed into spatio-temporal representations (target trajectories). For the adult writer, this transformation is assumed to be automatized or 'overlearned' for the strokes within an allograph, i.e., the strokes that are merged in a fixed context. However, the temporal representation of a single allograph is also to be embedded in the current movement context and linked to its neighbors by connecting strokes and/or pen-up movements. This task places a separate demand on the information processing capacities at this stage. There is some experimental evidence to support this view (Meulenbroek & van Galen, 1989). Thus, during writing, a decision process will be active that determines the best connecting strategy, given two successive allographs.
It should be noted that at this level, there is as yet no specification of the eventual end effector. The output of our model is a target trajectory in 3-D space. This choice is based on evidence that the planning of movements indeed takes place in a 3-D representation of the outside world as opposed to planning in intracorporal joint space. For instance, Hollerbach and Flash (1981) calculated the trajectory deviations caused by Coriolis forces that can be expected theoretically in fast targeting movements. On the basis of the near-rectilinear experimental hand trajectories they conclude that an a priori adjustment in movement programming takes place to overcome the Coriolis disturbances and keep the hand movements rectilinear. The spatial trajectory of hand movements generally is more invariant and less complex than the course of individual joint rotations in time (Morasso, 1986). This principle is assumed to be of ecological significance in the planning of movements in the same space as in that where objects and obstacles are located. Planning in joint space would lead to a large variability in the trajectory of the end effector which interferes severely with requirements as regards collision avoidance and minimization of inertial force in object handling. It should be noted that this does not hold for all motor tasks. Consider, for instance, other actions than the free planar pen-tip movement in handwriting or 3-dimensional pointing movements, where planning in joint space actually is required, e.g., in isometric force appliance to an object held with two hands, or the holding of the pen by several fingers in handwriting.
The description of the pen tip trajectory in an internal spatio-temporal representation constitutes the bottom range of the scope of the current model. Of course, the authors do not claim to know in what form these representations actually exist in the motor system, but they strongly believe there must be a fluent spatio-temporal representation of movements. So, it is doubted whether the nervous system enjoys any special advantages by using bang-bang or staircase-typed movement representations (Dooijes, 1984; Plamondon & Lamarche, 1986). Although, at the lowest level, motor unit contractions (twitches) are indeed discrete events, the nervous system uses the mechanisms of firing rate control and recruitment of a large number of motor units (van Boxtel & Schomaker, 1983) to produce continuously varying muscle excitation. It is only then that mechanical damping (read: filtering) takes place.
Still lower levels in the motor system would have to handle the problem of the conversion from 3-D internalized space to n-dimensional joint space, such that the chosen end effector will follow the prescribed trajectory and forcing pattern in external 3-D space: the problem of inverse kinematics and inverse dynamics transformations (Asada & Slotine, 1986). The final stage would be the specification of the excitability pattern for the alpha and gamma-motoneuron pools of the involved muscles.
Since a neural information processing system is plagued by a continuous stream of interoceptive and exteroceptive noise, and since it is confronted with real-world mechanics in the final stage (friction, hysteresis and writing-surface irregularities) feedback loops will exist, returning information to higher levels, or operating within a given level. At the level of our model, visual or proprioceptive feedback delays are estimated to exceed the maximum delay for continuous control. Thus, position information that is fed back to the operating level of the model can only be used in reprogramming subsequent strokes. A stroke currently in production cannot be modified: it is assumed to be produced ballistically.
After having located the current model within the global system for handwriting production, we will now focus on the requirements and constraints for this model. The type of handwriting that is to be simulated is the ballistic, fluent handwriting of an experienced adult writer. This restriction allows us to disregard the complex problems involved in motor-learning processes. The point of departure thus is a 'status of the system' in which the writer has at his disposal a number of stable spatial representations of allographs, as well as a sufficient amount of motor experience to translate these spatial representations into movements of a given end effector.
Input to the model will be chains consisting of allograph symbols for lower and upper case letters, blanks and an occasional period or comma. These symbols are viewed as the parallel of internal abstract categories available within the neuronal system. Output of the model will be a specification of the planar target trajectory of the pen tip. Pen-lifting movements along the Z axis are reduced to a binary signal (pen up/down). A feedback mechanism will be used to maintain the orientation of the generated target trajectory. With respect to stroke parameterization and representation, the aim is to use a parsimonious topological description. We will now proceed to discuss the model from bottom up.
Already in early simulation studies it became apparent that the timing of movement units is an essential determinant of handwriting (Denier van der Gon & Thuring, 1965; Vredenbregt & Koster, 1971). When we look at the vertical and horizontal velocity components we see a pattern of low-frequency content near-sinusoidals of varying amplitude and period, only disturbed by a moderate amount of noise (Figure 1).
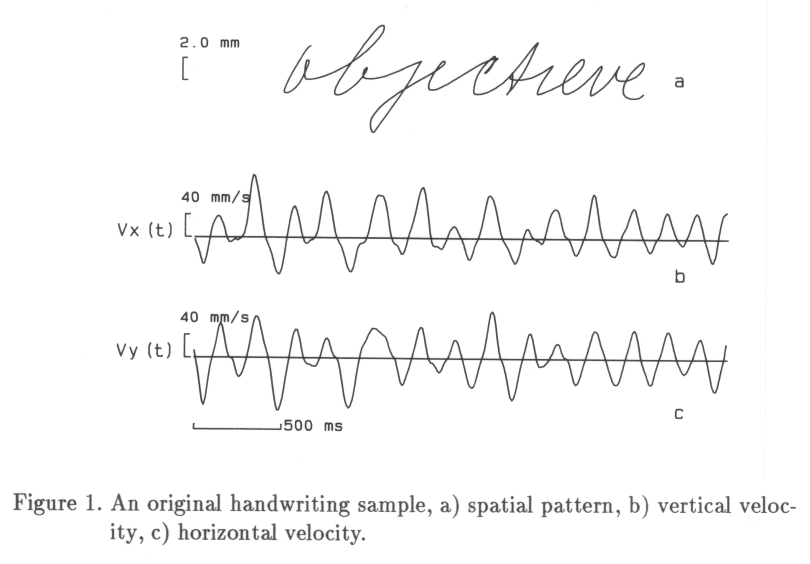
Sometimes the zero crossings in both signals coincide, sometimes the horizontal component (vx) lags the vertical component (vy) and vice versa. Thus, according to one hypothesis, handwriting is produced by modulating a horizontal and a vertical mass-spring oscillator (Hollerbach, 1981). Apart from the fact that such a model requires a considerable number of parameters (i.e., 13), to account for slant and size constancy, there are indications that modulated oscillation is not the type of motor control that the writer uses. In the first place, in our experiments, writers experience considerable difficulty in producing simple repetitive patterns like or for a sustained period of time (longer than 2 seconds) without errors. One might expect that this simple kind of oscillation should be easy for a system that controls movement by amplitude and phase modulation. Second, size and timing variations occur very often in handwriting, i.e., on a discrete stroke-to-stroke basis, which seems to be contrary to the idea of a mechanical sinus oscillator. This argument is also supported by findings which show that the 'isogony' principle which is dependent upon sinusoidal oscillation holds for scribbling movements, but not for normal cursive handwriting (Thomassen & Teulings, 1985). A third objection comes from the fact that at movement onset we would need a special input forcing pattern for the oscillator (a mass-spring system) to achieve its spatial target pattern immediately from rest. The authors support the view of trajectory formation as a process of chaining discrete strokes (Morasso et al., 1983). However, unlike the stroke definition in (Morasso et al., 1983), which is essentially in polar coordinates, the stroke is defined here as a combined acceleration plus deceleration movement unit for a spatial axis in Cartesian space. The basic shape of such a stroke is (near) sinusoidal in the velocity domain (Figure 1). In cursive handwriting, at least two such corresponding momentum impulses (Maarse, 1987; Plamondon & Maarse, 1987) are needed for the production of a spatial stroke, one per spatial axis. Maarse (1987) compared a number of handwriting models. With respect to the quality of fit, velocity-domain models appeared superior. Included in the comparison were triangularly shaped momentum impulses and sinusoidally shaped momentum impulses. The latter signal type is used in the current project: it appeared to produce only a slightly lower quality of fit than the triangular signal type, which gave the best fit. In fact, careful observation of velocity profiles in human handwriting will reveal that the actual shape is something between triangular and sinusoidal (Teulings et al., 1986). It could be argued that the best approximation would be a filtered (damped) version of the synthetic and physically not realizable triangular momentum impulses. In order to avoid the choice of a filter transfer function, we will continue to use the sinusoidal momentum impulse as the fundamental movement unit in this model, until we know more about the physical origin of the small deviations between the observed and the simulated strokes.
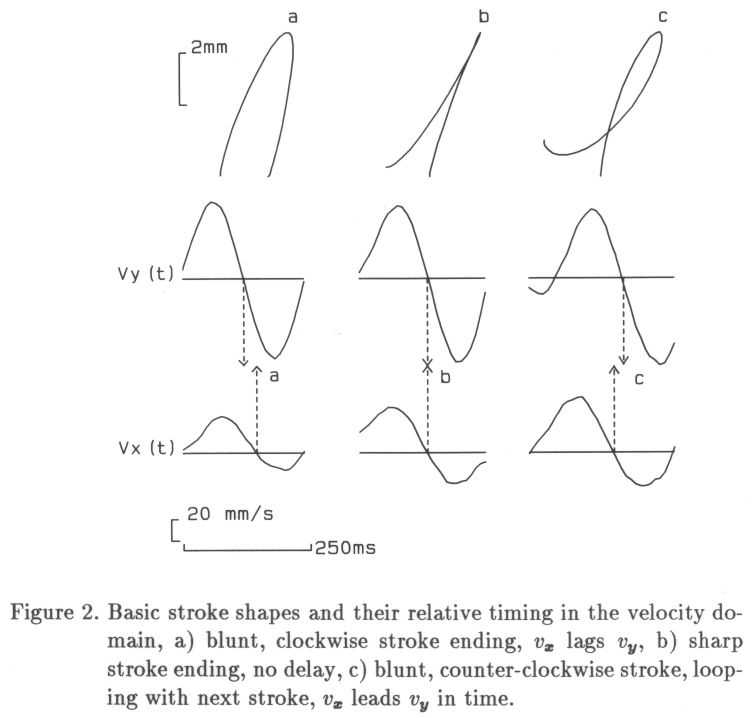
Figure 2 shows examples of the three basic stroke types in handwriting. The spatial up stroke is produced by horizontal and vertical momentum impulses of specified onset time, amplitude and duration. The vast majority of strokes in handwriting is of this type, with shapes varying gradually from very blunt and clockwise, via sharp, to very blunt and counter-clockwise, and looping. Since both X and Y impulses contribute to the same spatial stroke, they are considered to be 'locked', i.e., they are not independent in the sense that horizontal and vertical movements are considered to be independent 'signals' in other studies (Dooijes, 1984; Maarse, 1987). One could, for instance, as is done in many studies, parameterize the vx and vy signals by creating independent parameter lists for both directions, containing duration and amplitude of each sinusoid. After parameter evaluation and integration versus time one would obtain displacement functions containing regenerated sample of handwriting. Generation of new movements, however, implies that a system is producing movement components along each of the two or three orthogonal axes for a given discrete spatial stroke. Thus the parameterization method should account for the time allocation of momentum impulses corresponding to a spatial stroke. A straightforward and simple method is the following. The basic parameters are the required relative horizontal and vertical displacement in space, DX and DY, of a movement section which we call a 'compound stroke'. Times of occurrence of zero crossings in the vx and vy signals determine the points in time at which the spatial distances, DX and DY, respectively, can be determined. This deals with the displacement per se. The remaining characteristics to be parameterized are the impulse durations and the shape at the stroke ending (Figure 2, points a, b and c). As can be seen from this figure, shape could be described by the time delay between the two vx and vy zero crossings. We then would need three parameters in addition to DX and DY, viz., the durations of both momentum impulses and a time delay parameter. However, if the momentum impulses indeed belong together and are produced by the same pacing mechanism we can also assume the following. The duration of the execution of a single spatial stroke, as derived from the standard segmentation of the tangential velocity signal (Teulings et al., 1987), will be the basis for the durations of the vx and vy momentum impulses, Tx and Ty respectively. So we take the compound stroke duration T as the third parameter. In a given sample of handwriting, it can be estimated by measuring the time between two minima in the tangential velocity, or simply by taking the average (Tx+Ty)/2. Instead of taking the physical time delay as the fourth parameter, we now introduce a shape parameter C which is the proportion delay of the given compound duration T, to be achieved at stroke ending. Parameter C is comparable to the concept of 'phase', but it has the advantage of not being related to the concept of oscillation. C can attain positive or negative values, roughly varying from -1.5 (counter-clockwise) to +1.5 (clockwise). With this method, smoothness of the transition between two strokes depends on the overlap in time of the two movement components.
| Parameter | Name | Unit | |
| 1 | DX | relative horizontal displacement | mm |
| 2 | DY | relative vertical displacement | mm |
| 3 | T | duration (Tx+Ty)/2 | ms |
| 4 | C | shape factor (tvx = 0 - tvy = 0)/T |
Table 1. An overview of the used stroke parameters.
The duration parameter T can be made relative itself if it is expressed as a proportion of the period of the required average stroke pacing, thereby deferring the introduction of physical time to a later stage of processing. In the current model, however, we will express T in absolute terms. Note that the proposed stroke parameterization only determines the shape of the stroke ending. The curvature of a stroke's beginning is completely determined by its predecessor. Thus, a curvilinear shape of an initial stroke in a word is characterized by a preceding stroke for which holds: DX = 0, DY = 0, C ¹ 0, T > 0. The proposed method allows for a context-sensitive and parsimonious stroke modeling that is suited for use at the bottom level of the generator, where the target trajectory is compiled. Furthermore, it allows for a selective global biasing of each of the parameters, for example to induce sharper or rounder letter shapes by multiplying parameter C with some factor. Now we will proceed with the higher levels of the current model.
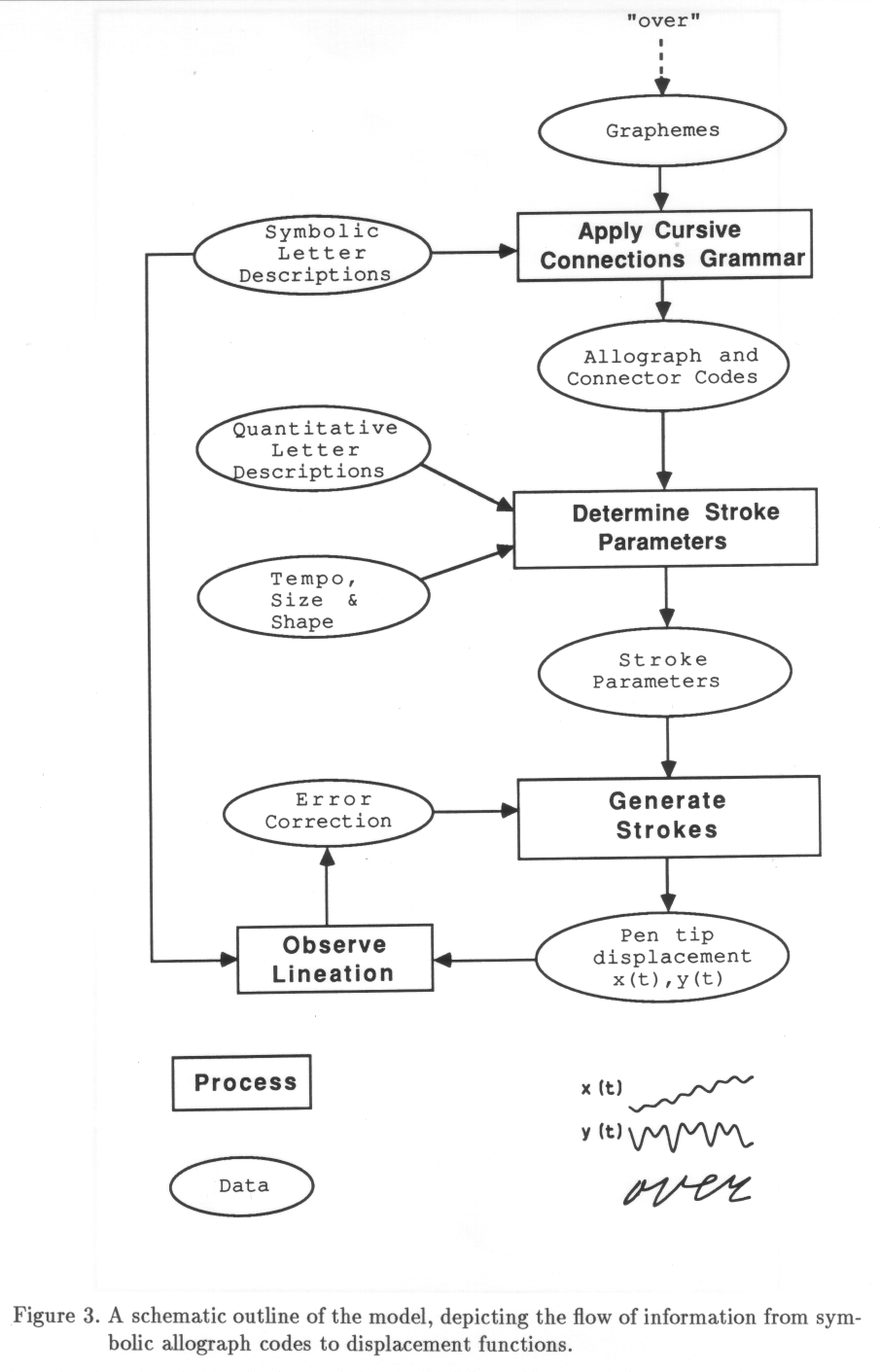
Figure 3 gives an overview of the data structures and the data processing modules of the model. The incoming data are allograph symbols. They will be converted stepwise into a quantitative form.
The first step is to insert symbols for connecting strokes and pen-lifting strokes between the allographs. This is done by the Cursive Connections Grammar (CCG). The CCG can be understood as a 'Production System' (Witteveen, 1984) with rules such as:
<ALPHA><ALPHA> :== <ALPHA><CONNECTOR><ALPHA>
<ALPHA><PENUP> :== <ALPHA><ENDSTROKE><PENUP>
<ALPHA><PUNCT> :== <ALPHA><ENDSTROKE><PUNCT>
<PENUP><ALPHA> :== <PENUP><BEGINSTROKE><ALPHA>
<ENDSTROKE><*> :== <ENDSTROKE><PENUP><*>
<*><PUNCT> :== <*><PENUP><PUNCT>
where <ALPHA> stands for 'a symbol belonging to the set of
alphabetic symbols', <*> stands for any symbol, etc.
Connecting strokes (or <CONNECTOR>s as termed above), are the pieces
of handwriting, normally starting at about the base line
or descender
line and completing the shape of the current letter, spanning the
horizontal distance to the next letter and initializing the shape
of this next letter. The rules shown above, tell us to insert
connecting strokes between two alphabetics, to append small ending strokes if
we are at the verge of a pen-up movement, and to lift the pen if
there is a punctuation sign coming. The CCG is applied recursively
to an incoming pair of symbols and it inserts pieces until no
rule has an effect any more. To be able to substitute the generated
insertion symbols, the CCG consults a qualitative (ordinal)
description of allographs: the Symbolic Letter Description. This is
a grid of available spatial vertical and horizontal levels and
levels of curvature. For instance, going from an to an
requires a connecting stroke from to ,
and with .
The resulting symbol chains enter the
Stroke Parameterization
process (step two), where they are further refined and converted
into a sequence of stroke parameters, that are biased by the
global setting of the tempo, size and shape factors. The
refinement is achieved by consulting the Quantitative Letter
Description, a more accurate but less general parallel of the
Symbolic Letter Description.
The third and final step is the
distribution of available
time for a spatial stroke among momentum impulses along the X
and Y axis according to the required size and shape by the
Stroke Generator. The output of the Stroke Generator is
monitored by a process that uses the Symbolic Letter Descriptions
as a lineation reference. This is necessary because the position
data have to be updated in the correct cells of a memory of the
lineation that has actually been produced until now. This memory is of
the exponentially decaying type. If an already
generated stroke
deviates too much from the current state of the lineation memory,
the programming of the size of the subsequent stroke is adjusted.
The architecture of a computational model of any aspect of human behavior is fundamental to its plausibility. The architecture of the current model is built upon the concept of a continuous flow of the smallest chunks of information possible through a hierarchically constructed set of operations. The opposite view would be that of a sequence of operations on larger information units such as complete words or sentences. There are some arguments against the latter approach. In the first place, it would be a severe limitation of the model if it would operate word by word only: we know that the human writer can write cursive words that are dictated by spelling letter by letter. A speaker generally has to wait until more "letters" are known since phonemes encompass a much larger context than graphemes do. Indeed, there are some indications that the scope of motor context in handwriting may be much smaller than in speech. In handwriting there is nothing like the intonation in speech (pitch envelope) which is semantically important and can only be produced if several words are known beforehand. Therefore we would like to restrict the extent of the motor context in the handwriting generator as much as possible until empirical evidence commands the contrary. In the current model, motor context is confined to a range of strokes that belong to two letters only (Hulstijn & van Galen, 1983). An architecture like this, working with such small chunks of information at a time can easily be made context sensitive at all levels by insertion of context-dependent steps of processing within the hierarchy. A stepwise, block-oriented model, on the contrary, can not be set to operate on chunks of information smaller than the minimum size (e.g. word by word). Much like the human information processor, the current model starts operating on the smallest amount of information coming in and passes it to lower levels of processing. The active levels will process down-flowing data only if there is insufficient context available to complete the ongoing operations, thus working on an 'as needed' basis. We will proceed to describe how a working model is built and make some comparisons between simulated and original handwriting samples.
2 Methods
The generation parameters are based on a page of handwriting (12 lines, 75 words, 230 seconds duration) of a very experienced and 'regular' writer (male, righthanded, age 44). Furthermore, use is made of a continuously growing corpus of recorded handwriting samples of several subjects (righthanded, age 18 years and older) to test the analysis procedures.
Pen tip displacement signals were recorded by means of a large-size writing tablet (Calcomp 9240), sampling frequency 105 Hz, spatial resolution 0.025 mm, or by means of a medium-size tablet (Vector General), sampling frequency 100 Hz, resolution 0.02 mm. The analog axial pen pressure was digitized (10bits, 1g/bit) synchronously with the displacement data. Unless stated otherwise, the displacement data are off-line digitally low-pass filtered with a FIR filter with 25 weights and a transition band from 10 to 30 Hz (Rabiner & Gold, 1975). The displacement signals (Sx and Sy) are differentiated by means of a five-weight FIR window (Dooijes, 1984) to obtain horizontal (vx) and vertical (vy) velocity signals. The pen pressure signal is used to obtain reliable pen up/down information.
The first step is to analyze histograms of the spatial positions of vertical extrema. The recorded handwriting data should have horizontal orientation, either by a proper recording procedure or by post-hoc numerical rotation. Separate lines of handwriting are extracted. To obtain reliable histogram peaks, the lines should contain a sufficient amount of body size points as in , descender points as in and ascender points as in (Figure 4). The histogram of the Y minima will show a distinct peak indicating the position of the base line of handwriting (Y0). To
the left of this large peak there will be some small peak indicating the position of the descender line (Yd). The histogram of the Y maxima will show a clear peak at the level of the body-size line (Yb). To the right of this large peak there will be some peaks indicating ascender line positions (Ya). The body-size size can be estimated reliably by
| (1) |
Because there will be much less descender and ascender samples in a piece of cursive script than base line and body-size line samples, estimates of descender and ascender size will be less reliable. The descender size is determined by
| (2) |
and the ascender size by
| (3) |
The ratios Ha/Hb and Hd/Hb will be characteristic for the writings of the subject in question. The method described has indeed been used successfully in a study on writer identification (Maarse et al, 1986). Other, slightly more subtle, characteristic levels in lineation are the global maxima in the global minima in , and the positions of dots on and which tend to be much more variable. Analysis of several handwriting samples revealed a lineation that reflects the handwriting method taught at primary school. Deviations often comprise overshoots and undershoots in the first and last strokes of words, respectively. An even more detailed refinement is obtained by observing the handwriting more closely. Between the base line and the body-size line, three levels may be identified, indicating endings of terminal strokes, intermediate levels (as in , cursive ) and starting points of initial strokes, respectively. Depending on the individual writer, these levels may coincide, or additional levels may be present. The identified levels are given an ordinal number and a corresponding symbolic name. The handwriting sample used in this study contained 10 levels of lineation (Table 2).
Table 2. An example of the ordinal classes of stroke
characteristics in the symbolic stage, and
their names. This 'grid' is used by the
Cursive Connections Grammar to build connecting
stroke codes.
DEFINE
LINEATION:
Low (minimum in <g>, <j>)
Low-PLUS (minimum in <p>, <q>)
Base-line-MINUS
Base-line (minima in <m>)
Base-line-PLUS
Intermediate
Mid-line (maxima in <m>)
Mid-line-PLUS
Upper-line-MINUS (maximum in <t>, <d>)
Upper (maximum in <k>)
SHAPES:
Negative (counter-clockwise)
Sharp
Positive (clockwise)
PROGRESSION:
Close
Normal
Far
PENSTATUS:
Down
Up
END
Coding example for a connecting stroke:
(b_m_p_c) = 'from Base to Mid, clockwise (p) and Close'
Within letters, a wide range of stroke ending curvatures is found. Since the fine-grained within-letter shape is not needed in the symbolic stage, we leave the stroke shape definition within letters to the quantitative stage. For the connecting strokes, as a rough approximation, only three levels of the shape of connecting strokes were sufficient for the writer under study: counter-clockwise as in a connecting stroke leading to , sharp as in a connecting stroke leading to and clockwise as in a connecting stroke leading to .
Here also, a coarse categorization in three levels of horizontal progression between letters is sufficient: Close, Normal and Far. Since the vertical and horizontal sizes of connecting strokes are strongly coupled (typically, r=0.9), this categorization is relative to the vertical size of a stroke.
Preprocessing involves low-pass filtering and segmentation. The aim is to find the corresponding vx and vy momentum impulses for each spatial stroke, which is not trivial. This is done by means of an algorithm that indicates possible corresponding vx and vy momentum impulses and allows the operator to correct misalignments. The success of this operation depends upon the percentage of hesitations or slow correcting movements (graphical editing) in the handwriting sample. Since the model describes ballistic movements, samples containing severe movement artefacts are excluded from the analyses. Residual shortlasting (i.e., shorter than 30 ms) local disturbances that cause misalignment are solved by applying additional local filtering with a simple first-order recursive filter ( y(k) = ax(k) + beta y(k-1), a = b = 0.5). This procedure guarantees that no overall filtering bias is imposed on the signal at moments where no segmentation difficulties arise. Another source of segmentation difficulty is the projection of the movements onto the orthogonal axes of the tablet. If the direction of a ballistic stroke coincides with one of the axes of the tablet, the movement residual in the orthonormal direction will be irregular. Such problems can be avoided by determining the preferred axes of handwriting beforehand (Denier van der Gon, & Thuring, 1965; Teulings et al., 1989). When the correct segmentation points are known, the four stroke parameters DX, DY, C and T are calculated. Stroke sizes DX and DY are calculated by numerically integrating the corresponding vx and vy strokes. Moments of zero crossings (tvx = 0 and tvy = 0) are inversely interpolated and used to obtain stroke durations Tx and Ty. The 'compound' stroke duration is approximated by
| (4) |
The shape factor C is determined by the time difference between the zero crossings in vx and vy, i.e.:
| (5) |
In the generation process, this parameterization results in dividing the available time T for the compound stroke equally over the separate axes, such that the delay at the stroke ending is as prescribed:
| (6) |
| (7) |
| (8) |
| (9) |
where
$\Delta t_{b}$ is the delay between the velocity zero crossings of both axes at the beginning of the stroke,
$\Delta t_{e}$ is the requested delay of the velocity zero
crossings of both axes at the ending of the stroke,
$T'_{x}$ is the duration of the vx momentum impulse,
$T'_{y}$ is the duration of the vy momentum impulse.
3 Results
The construction of the letter description data structures (by lineation analysis, analysis of shape and analysis of horizontal progression) for the writer under study did not pose any special problems. In building the quantitative letter and stroke definitions, non-cursive letters or letters containing editing movements were excluded (two s, which were in block print, and two out of 26 s, also of block print type, with pen-lifting). There were no other allograph variations.
Table 3. Letter frequencies.
a (13), b (10), c (10), d (21), e (97), f (5), g (13),
h (11), i (29), j (1), k (8), l (14), m (7), n (48),
o (22), p (9), q (1), r (19), s (20), t (26), u (8),
v (12), w (5), x (1), y (4), z (1), D (3), H (2),
Z (1).
Frequencies of pen-lifting and special movements are: blank spaces (61), commas (5), periods(4), dottings (30), editing (2), long-lasting blanks (2), new line movements (11), other pen liftings (12). Table 4 presents a sample of transformations at the symbolic stage, produced by the Cursive Connections Grammar. Note the inserted codes for connecting strokes and pen-lifting movements. Also note the crude approximation of horizontal progression for spaces between words, (space) denoting the default horizontal progression, (spacef) indicating movements above the paper, 'landing' somewhat more to the right. As can be seen, the connectors are generic, no reference is made to the surrounding allograph codes within the connector codes themselves.
Table 4. A sample of input and output to the Cursive Connections
Grammar, a) input text, b) output codes. See table 2
for an explanation of the used codes.
a) ...an adequate language does not exist.
b) ...(a)(b_m_p_c)(n)(b_bplus_s_c)(spacef)(a)(b_m_s)(d)(b_m_n)
(e)(b_m_p)(q)(lplus_m_s_c)(u)(b_m_s)(a)(b_uminus_s)(t)(i_m_n)
(e)(b_bplus_s_c)(space)(i_u_n)(l)(b_m_s)(a)(b_m_p_c)(n)(b_m_s)
(g)(l_m_s_c)(u)(b_m_s)(a)(b_m_s)(g)(l_m_n)(e)(b_bplus_s_c)
(spacef)(d)(b_m_s_c)(o)(m_m_n)(e)(b_m_p_c)(s)(space)(i_m_p_c)
(n)(b_m_s_c)(o)(m_uminus_s)(t)(i_i_s_c)(space)(i_m_n)(e)
(b_m_s_c)(x)(b_m_s_c)(i)(b_m_p_c)(s)(b_uminus_s)(t)(i_i_s_c)
(penup_pendown)(period)
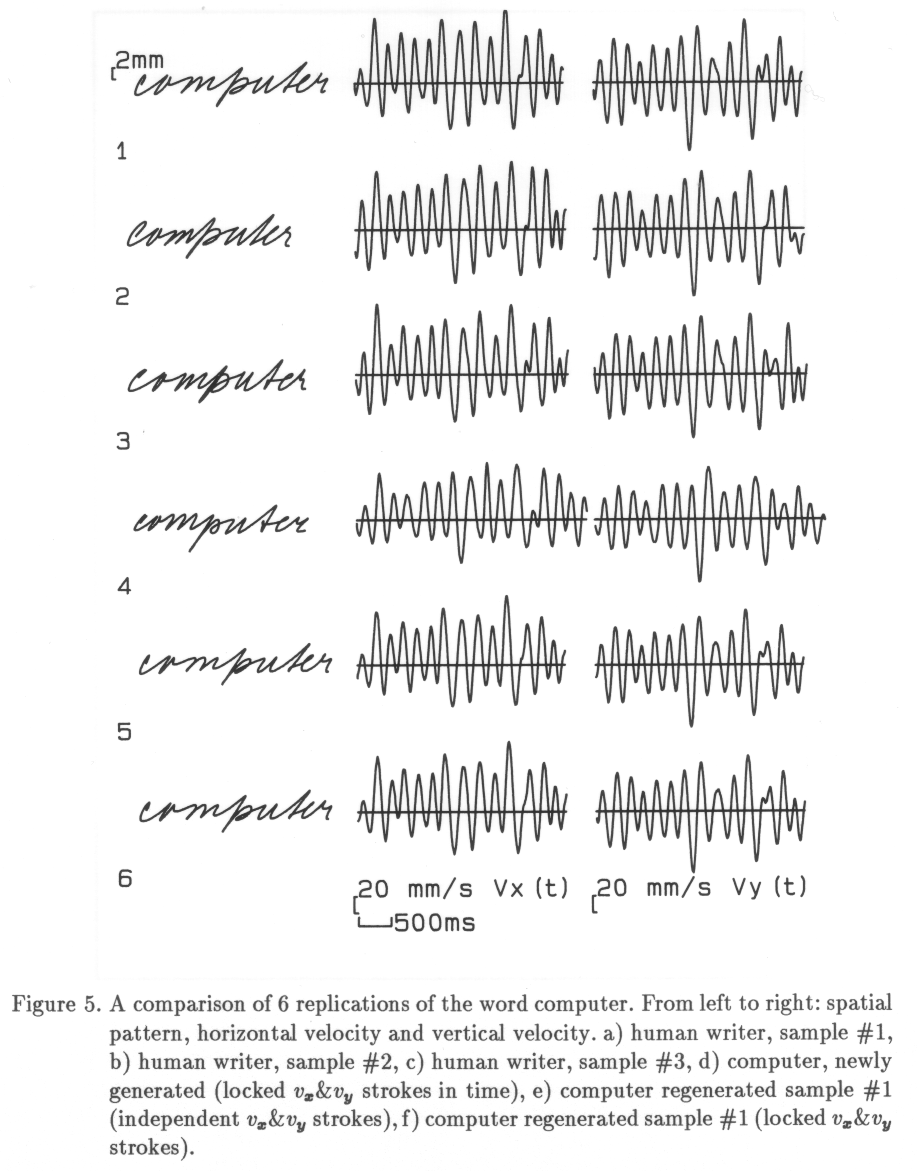
Figure 5 shows a comparison between some replications of the word 'computer'. The first three replications are originally written by the subject. The fourth sample is newly generated by the model. The fifth sample is a regenerated version of the first word, by parameterizing the horizontal and vertical momentum impulses independently, as in (Maarse, 1987). The sixth sample is also a regenerated version of the first word, but in this case, stroke parameterization was done by locked corresponding X/Y momentum impulses, as in the generator model.
Table 5 presents a numerical account of the differences between the horizontal stroke sizes of the 6 replications. It appears that on the average, the model produces horizontal connections (4) that are 0.2 mm shorter than the subject did (1-3). From the correlation table it appears that the model (4) does not produce strong deviations from the originals. As to be expected, regenerated versions (5) and (6) strongly resemble the original (1). Also, versions (5) and (6) are highly equivalent, which shows that the method of 'locked' momentum impulses does not produce deviations from regeneration by independent vx and vy momentum impulses.
Table 5. Comparisons of horizontal stroke size.
Mean and standard deviation (mm)
m s N
1 2.947 1.896 30
2 2.951 1.809 31
3 2.928 1.847 30
4 2.429 1.606 32
5 2.706 1.850 30
6 2.683 1.840 30
Correlation, N=30
1 1.000
2 0.742 1.000
3 0.989 0.744 1.000
4 0.934 0.717 0.917 1.000
5 1.000 0.741 0.988 0.933 1.000
6 1.000 0.744 0.988 0.932 1.000 1.000
Standard deviation of differences (Rows minus Columns)
1 0.000
2 2.432 0.000
3 0.497 2.417 0.000
4 1.231 2.408 1.355 0.000
5 0.258 2.364 0.560 1.121 0.000
6 0.278 2.347 0.555 1.121 0.056 0.000
Legend:
1-3 Original handwriting samples
4 Newly generated sample
5 Regenerated version of 1, by independent vx & vy
6 Regenerated version of 1, by locked vx & vy
Table 6 shows the comparisons of the vertical stroke sizes for all replications. On the average, the generated vertical strokes (4) are again somewhat smaller than the original vertical strokes. It appears that correlations between the vertical stroke sizes are higher than those between horizontal stroke sizes. The newly generated replication does not deviate significantly from the originals (1-3).
Table 6. Comparisons of vertical stroke size.
Mean and standard deviation (mm)
m s N
1 2.785 1.369 30
2 3.044 1.338 28
3 2.665 1.476 32
4 2.460 1.347 32
5 2.554 1.320 30
6 2.529 1.298 30
Correlation, N=28
1 1.000
2 0.990 1.000
3 0.966 0.967 1.000
4 0.970 0.970 0.989 1.000
5 1.000 0.988 0.965 0.969 1.000
6 1.000 0.989 0.966 0.970 1.000 1.000
Standard deviation of differences (Rows minus Columns)
1 0.000
2 0.490 0.000
3 0.826 0.854 0.000
4 0.789 0.861 0.516 0.000
5 0.254 0.617 0.834 0.726 0.000
6 0.282 0.619 0.825 0.717 0.054 0.000
Table 7 shows the comparisons of the horizontal stroke durations. From the average durations we can see that the generated strokes (4) lasted somewhat longer than the original strokes (1-3). From the correlation matrix we can see that in the comparisons (1-4), correlations are much lower than in the case of horizontal stroke size . The originals (1) and (3) appear to intercorrelate highly, whereas the original (2) and the model (4) are moderately intercorrelated.
Table 7. Comparisons of horizontal stroke duration.
Mean and standard deviation (ms)
m s N
1 105.857 26.728 29
2 103.463 26.617 30
3 107.959 30.891 29
4 108.439 26.797 31
5 105.397 31.094 29
6 105.890 31.653 29
Correlation, N=29
1 1.000
2 0.352 1.000
3 0.942 0.346 1.000
4 0.435 0.613 0.378 1.000
5 0.967 0.429 0.877 0.532 1.000
6 0.966 0.440 0.887 0.545 0.996 1.000
Standard deviation of differences (Rows minus Columns)
1 0.000
2 29.999 0.000
3 10.641 32.752 0.000
4 28.919 23.647 32.759 0.000
5 8.589 30.792 15.354 28.595 0.000
6 9.073 30.879 14.883 28.518 2.963 0.000
Table 8 shows the comparisons of the vertical stroke durations. From the average durations we can see that the generated strokes (4) take an intermediate position with respect to the original strokes (1-3). Here correlations are of even lower value than in the case of the horizontal stroke durations. The model (4) produces vertical strokes with durations that covary most closely with the original (3), the lowest correlations exist between the model (4) and the original (1).
Table 8. Comparisons of vertical stroke duration.
Mean and standard deviation (ms)
m s N
1 106.538 24.517 29
2 116.430 27.434 27
3 102.033 24.758 31
4 109.416 18.348 31
5 106.430 24.952 29
6 106.941 24.670 29
Correlation, N=27
1 1.000
2 0.512 1.000
3 0.361 0.288 1.000
4 0.171 0.236 0.715 1.000
5 0.976 0.501 0.329 0.206 1.000
6 0.974 0.520 0.406 0.261 0.990 1.000
Standard deviation of differences (Rows minus Columns)
1 0.000
2 25.529 0.000
3 26.276 30.071 0.000
4 27.207 28.942 15.849 0.000
5 5.300 25.872 27.013 26.780 0.000
6 5.386 25.218 25.176 25.577 3.342 0.000

Figure 6 shows a longer sample of spatial output of the model. At first sight the data give the impression of some 'naturalness': there are no evident artificial-looking shape repetitions. A given letter may differ in shape according to the context (e.g., or ). However, closer observation reveals some peculiarities. Some connecting strokes do not seem to be fully appropriate. Moreover, horizontal progression between words is a little coarse. In some strokes, finally, inflection points might be expected, as discussed in an earlier paper (Schomaker & Thomassen, 1986).
4 Discussion
Even with the parsimonious parameterization used, we have already obtained a reasonable approximation of the subject's handwriting in the spatial and temporal domain. From the comparisons made, provisional conclusions may be drawn. Again, spatial (size) consistency appears to be higher than temporal (duration) consistency in the comparisons of the three original words and a generated word. A striking finding is that the locked parameterization of momentum impulses proposed in this study does not lower the correlation with the original data as compared to an independent parameterization of horizontal and vertical velocity. In the spatial domain, between-letter context effects are present that resemble the handwriting of the original writer. The used lineation grid enables the model to maintain a horizontal baseline and to generate an estimate of the vertical position of the next pen-down position for new words. However, some qualifying comments must be made here. In the current state of the model, connecting strokes are generic, i.e., the - transition is considered to be the same as the - transition. This does not seem to be justified in all cases. It might be that in fact the human writer makes more use of stored connecting strategies for different allographic contexts, or performs more 'real-time' computation to program (connecting) strokes. In the former case, we would have to add transitions to the Cursive Connections Grammar and update the Symbolic and Quantitative stroke definitions. In the latter case, the Stroke Generator module should be made more sensitive to the current motor context. Such a solution would also make it possible to let the Stroke Generator reprogram strokes in case of changes of movement direction from clockwise to counter-clockwise and vice versa. The human writer shows a strategy where the stroke with the longest duration shows a short deceleration in these cases (Schomaker & Thomassen, 1986). Also, some bigrams might in fact be overlearned to such an extent that we should consider them to be part of a single two-letter allograph: a digraph. The horizontal progression between words can be made more natural by refining the grid of horizontal progressions. This can be done by further analyses on the histograms of horizontal stroke sizes. Also, what is needed is knowledge on the subtle perceptual cues that the writer uses in planning horizontal progression. In computer graphics, for instance, the designer of letter fonts defines 'hot spots' as anchor points for spatial concatenation. Probably such 'spots' also exist in handwriting curves. An interesting extension of the current model would be a top level that takes care of context-dependent allograph selection. Such an extension is only feasible if a large corpus of handwriting of a writer is available. In the recorded samples of handwriting (one page per subject) that the authors have available, however, most writers do not seem to exhibit a sufficiently consistent use of different allographs for formal rules to be derived. At the bottom level, a promising continuation of the current work would be the use of K-nets (Kinematic Nets) (Morasso & Mussa Ivaldi, 1987), a formalism that enables the solution to the inverse kinematics problem, to specify the joint and, eventually, muscle-domain control patterns for a given end effector. The advantage of this approach is the natural inclusion of dynamics (forces) in the movement control on the basis of the task-related demands in handwriting, i.e., producing a planar trajectory while applying sufficient force to produce a legible trace on the writing surface. Another point of discussion is the use of a Cartesian coordinate system at this level of movement planning. Some would argue that coding in terms of polar coordinates is more attractive in terms of rotation invariance. Although we do not really know how movement patterns are represented in the brain, there are some theoretical and practical considerations that support the choice of an orthogonal coordinate system as the frame of reference when planning external 3-D movements. Here, I would like to quote Denier van der Gon & Thuring (1965): 'the occurrence of perpendicular directions in biology and physiology is well-known, for instance the analysis mechanism of the semi-circular canals' (in the vestibular system). In (Denier van der Gon & Thuring, 1965) also, reference is made to the work of Dal Bianco in the 1940s who showed that cerebellar lesions can have specific consequences for movements in one orthogonal plane. A practical objection to the use of a running angle representation would be its dependency on the initial value and the propagation of direction errors in time. With respect to the architecture of the model, the following remarks can be made. We are confronted with a very complex real-life system on the one hand and the current 'paradigms' in science, as well as the 'state of the art' in technology on the other hand. These two latter aspects determine what is 'thinkable' and what is not. The terminology used, the processing steps indicated and the solutions that are proposed in this paper serve to guide our conceptualization of the handwriting process (cf. figure 3). Thus, a 'cognitive' module like the Cursive Connections Grammar can be implemented as a formal production system, as it is done in this study, or it could just as well be implemented as a neural network simulation in connectionist terms, as proposed in (Morasso & Mussa Ivaldi, 1987). In our view, the connectionist approach is appealing because of the somewhat more (bio)physical and physiological nature of the models involved. On the other hand, the danger exists that basic information processing steps are obscured in this approach, by relegating basic processes to a single artificial neural network that solves the demanded input/output relationships. Methodologically, a better procedure for matching model data with original handwriting might be one which uses dynamic programming to find a time warp function of the handwriting samples for an optimal alignment in time (Brault & Plamondon, 1987). Finally, we would like to mention the use of the proposed model as a synthesis stage within cursive-script recognition, which is under study in ESPRIT project P419 (Teulings et al., 1987).
5 References
Asada, H., & Slotine, J.-J.E. (1986). Robot analysis and control. New York: Wiley.
Brault, J.J., & Plamondon, R. (1987). Global and local time warping function for handwritten curves comparison. In R. Plamondon, C.Y. Suen, J.-G. Deschênes, & G. Poulin (Eds.), Proceedings of the Third International Symposium on Handwriting and Computer Applications (pp. 56-58). Montreal: Ecole Polytechnique.
Denier van der Gon, J.J., Thuring, J.P., & Strackee, J. (1962). A handwriting simulator, Physics in Medicine and Biology, 6, 407-414.
Denier van der Gon, J.J., & Thuring, J.PH. (1965). The guiding of human writing movements, Kybernetik, 2, 145-148
Dooijes, E.H. (1984). Analysis of handwriting movements. Doctoral dissertation. Amsterdam: University of Amsterdam.
Ellis, A.W., (1986). Modeling the writing process. In G. Denes, C. Semenza, P. Bisiacchi & E. Andreewsky (Eds.), Perspectives in cognitive neuropsychology, London: Erlbaum.
Hollerbach, J.M., & Flash, T., (1981). Dynamic interactions between limb segments during planar arm movement, AI memo No. 635, Massachusets Institute of Technology, Artificial Intelligence Laboratory, November.
Hollerbach, J.M. (1981). An oscillation theory of handwriting. Biological Cybernetics, 39, 139-156.
Hulstijn, W., & Van Galen, G.P. (1983). Programming in handwriting: Reaction time and movement time as a function of sequence length. Acta Psychologica, 54, 23-49.
Maarse, F.J., Schomaker, L.R.B., & Teulings, H.-L. (1986). Kenmerkende verschillen in individueel schrijfgedrag: automatische identificatie van schrijvers. (Characteristic differences in individual writing behavior: Automatic writer identification), Nederlands Tijdschrift voor de Psychologie, 41, 41-47.
Maarse, F.J., (1987). The study of handwriting movement: peripheral models and signal processing techniques, Doctoral dissertation, University of Nijmegen.
Meulenbroek, R.G.J., & Van Galen, G.P. (1989). The production of connecting strokes in cursive script: Developing co-articulation in 8 to 12 year-old children. In R. Plamondon, C.Y. Suen, & M.L. Simner (Eds.), Computer Recognition and Human Production of Handwriting (pp. 273-286). Singapore: World Scientific.
Morasso, P. (1986). Trajectory Formation. In Morasso, P. & Tagliasco, V. (Eds.), Human Movement Understanding. Amsterdam: North-Holland.
Morasso, P., & Mussa Ivaldi, F.A. (1987). Computational models of handwriting. In R. Plamondon, C.Y. Suen, J.-G. Deschênes, & G. Poulin (Eds.), Proceedings of the Third International Symposium on Handwriting and Computer Applications (pp. 8-9). Montreal: Ecole Polytechnique.
Morasso, P., Mussa Ivaldi, F.A., & Ruggiero, C. (1983). How a discontinuous mechanism can produce continous patterns in trajectory formation, Acta Psychologica, 54, 83-98.
Plamondon, R., & Lamarche, F. (1986). Modelization of handwriting: A system approach. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary Research in Handwriting pp. 169-183. Amsterdam: Elsevier.
Plamondon, R., & Maarse, F.J. (1987). A neuron oriented representation to compare biomechanical handwriting models. In R. Plamondon, C.Y. Suen, J.-G. Deschênes, & G. Poulin (Eds.), Proceedings of the Third International Symposium on Handwriting and Computer Applications (pp. 2-4). Montreal: Ecole Polytechnique.
Rabiner, L.R., & Gold, B. (1975). Theory and application of digital signal processing. Englewood Cliffs, NJ: Prentice-Hall.
Raibert, M.H. (1977). Motor control and learning by the state space model Doctoral dissertation, Massachusetts Institute of Technology.
Schomaker, L.R.B., & Thomassen, A.J.W.M. (1986). On the use and limitations of averaging handwriting signals. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 225-238). Amsterdam: North-Holland.
Teulings, H.L., & Maarse, F.J. (1984). Digital recording and processing of handwriting movements. Human Movement Science, 3, 193-217.
Teulings, H.-L., Thomassen, A.J.W.M., Schomaker, L.R.B., & Morasso, P. (1986). Experimental protocol for cursive script acquisition: The use of motor information for the automatic recognition of cursive script. Report 3.1.2., ESPRIT project P419.
Teulings, H.L., Thomassen, A.J.W.M., & Maarse, F.J. (1989). A description of handwriting in terms of main axes. In R. Plamondon, C.Y. Suen, & M.L. Simner (Eds.), Computer Recognition and Human Production of Handwriting (pp. 193-211). Singapore: World Scientific.
Teulings, H.L., Thomassen, A.J.W.M., & Van Galen, G.P. (1986). Invariants in handwriting: The information contained in a motor program. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary Research in Handwriting pp. 305-315. Amsterdam: Elsevier.
Thomassen, A.J.W.M., & Teulings, H.L. (1985). Time, size, and shape in handwriting: Exploring spatio-temporal relationships at different levels. In J.A. Michon & J.B. Jackson (Eds.), Time, mind, and behavior (pp. 253-263). Heidelberg: Springer.
Van Boxtel, A., & Schomaker, L.R.B. (1983). Motor unit firing rate during static contraction indicated by the surface EMG power spectrum. IEEE Transactions on Biomedical Engineering, 30, 601-609.
Vredenbregt, J., & Koster, W.G. (1971). Analysis and synthesis of handwriting, Philips Technical Review, 32, 73-78.
Witteveen, C. (1984). Programmed production systems, Doctoral dissertation, University of Utrecht, The Netherlands.
Chapter 4
Kinematics and kinetics
After having built a working model that describes the kinematical aspects of the pen-tip control problem, the question may be asked if kinematics is all there is in handwriting. Clearly, the movement is necessary to let the pen-tip travel along a path on the paper surface. However, there are other aspects in the writing task. A legible trace of regular thickness must be left behind by the pen. The paper or the pen must not be damaged by an applied force that is too large. The complex biomechanical end effector system that is not controlled along 3 orthogonal dimensions must follow the writing plane, without spending an overdue amount of muscular energy. Thus, force aspects, i.e., kinetics come into play, notably in the form of a compliance control problem. In this chapter, we try to find out if pen force is a passive dependent variable, determined by the kinematics of the movement and the parameters of the biomechanical system, or an actively controlled and independent control variable.
The Relation between Pen Force and Pen Point Kinematics in Handwriting. 6
Lambert R.B. Schomaker
Réjean Plamondon ·
Abstract
This study investigates the spectral coherence and time-domain correlation between pen pressure (axial pen force, APF) and several kinematic variables in drawing simple patterns and in writing cursive script. Two types of theories are prevalent: "biomechanical" and "central" explanations for the force variations during writing. Findings show that overall coherence is low ( < 0.5) and decreases with pattern complexity, attaining its lowest value in cursive script. Looking at subjects separately, it is found that only in a small minority of writers "biomechanical coupling" between force and displacement takes place in cursive handwriting, as indicated by moderate to high negative overall correlations. The majority of subjects displays low coherence and correlation between kinematics and APF. However, APF patterns in cursive script reveal a moderate to high replicatability, giving support to the notion of a "centrally" controlled pen pressure. The sign of the weak residual average correlation between APF and finger displacement, and between APF and wrist displacement is negative. This indicates that small biomechanical effects may be present, a relatively higher APF corresponding to finger flexion and wrist radial abduction. On the whole, however, variance in APF cannot be explained by kinematic variables. A motor task demanding mechanical impedance control, such as handwriting, apparently introduces a complexity that is not easily explained in terms of a passive mass-spring model of skeleto-muscular movement.
1 Introduction
Generally, researchers of handwriting movements in the fields of signature verification, forensic studies, and in biophysical or psychomotor studies have recognized the importance of the pen pressure 7 on the writing surface as an important dependent variable. For instance, in signature verification, the force exerted by the pen on the paper during handwriting appears to be a discriminating parameter between individual writers (Hale & Paganini, 1980; Crane & Ostrem, 1983; Deinet et al., 1987). Also, writer identification on the basis of normal handwriting samples is greatly improved if the pen-force signal is known (Maarse, Schomaker, & Teulings, 1986; 1988). Thus, in the writer identification or signature verification problem, the pen-force signal is an important source of information (Plamondon & Lorette, 1989). On the other hand, the number of studies exploring pen force is rather limited and little is known about the underlying control process.
Methods to measure pen force differ greatly. Sometimes, the pen force is measured directly with some kind of transducer during writing so that its time function is known. In the case where the transducer is mounted in the pen, and measures force along the longitudinal axis of the pen, we will speak about Axial Pen Force (APF). In the case where the transducer is located under the writing surface, normal pen force (NPF) is measured. In the latter case, the wrist is typically located on a separate supporting surface. At other times, as in forensic handwriting analysis, pen force is inferred from the static properties of the handwriting, i.e., trace thickness and depth (Baier et al., 1987) and the paper characteristics (Deinet et al., 1987), but the pen-force time function is not known. Another measure that is sometimes used is the pen-grip force (Kobayashi, 1981). In what follows, however, we will only be concerned with time-varying APF or NPF. Axial Pen Force and Normal Pen Force are related by:
| (1) |
A central question to be solved is the relationship between the pen-tip kinematics and the pen force. Essentially two viewpoints are relevant: the biomechanical hypothesis and the central control hypothesis.
In this view, the pen-force changes during writing are seen as a consequence of biomechanical factors related to the kinematics of the movements. Dooijes (1984) relates APF variations to the pen tip displacement in the vertical direction, supposedly brought about by the forefinger in many subjects which is "...pushing the pen into the paper surface during down strokes" (a stroke is generally defined as the trajectory segment between two consecutive minima in the tangential pen-tip velocity).
In this paper we would like to propose an approach that describes the pen force problem in terms of a mechanical impedance (Hogan, 1985) or compliance control problem (Asada & Slotine, 1986; Mason, 1982). A mechanical impedance is a system which accepts motion input and yields force output (Hogan, 1985). Suppose we wanted to let a robot system produce cursive script on some writing surface. We could define the motor task in terms of a pen-tip trajectory formation problem. In this situation the moving system has to control a lot of intra-corporal degrees of freedom (body df, bdf) in joint and actuator space. In the extra-corporal spatial domain, however, the movement in the air towards the writing surface demands the control of six (3 translational, 3 rotational) extra-corporal degrees of freedom (task df, tdf), while controlling zero degrees of freedom in the extra-corporal force domain since there is as yet no contact. However, at the moment of contact, making point-to-plane contact with the pen held in the end effector, the control problem is transformed into a five spatial tdf and one force tdf problem. The force is applied to the paper surface and compensated by a component, normal to the writing plane (NPF) and a frictional component along the writing plane. No torques are required by a point-to-plane contact. Clearly, the requirements of force control should be part of the motor task description. A possible description in handwriting is: äpply force in such a way that friction is overcome and a clear, legible trace is left behind". Thus, apart from the trajectory formation, mechanical impedance control is required. Since the writing system has to overcome surface (say, Coulomb) friction, additional force components have to be present along the X- and Y-axes, that are linearly related to NPF (Deinet et al., 1987). These additional force components complicate the control problem. There are task constraints, however, to make things easier for our robot. No rotation around the longitudinal pen axis is required for normal cursive script, so we can neglect this tdf. Furthermore, pen orientation does not have to be controlled explicitly (can be held approximately constant) since it is not part of the specific task requirements. In the human writer, the average orientation angle of the pen depends on hand anatomy and on personal preference, and variations seldom exceed a maximum amplitude of ten degrees in the normal cursive handwriting size, which is about 2.5 mm for an , on average. The movement system can concentrate on the pen tip's trajectory formation and on mechanical impedance, i.e., on regulating the normal pen force to produce a continuous trace of sufficient thickness and on overcoming friction in the XY plane by exerting an appropriate force along the X and Y axes.
According to a "pure" biomechanical hypothesis, variations in pen force are directly related to the peculiarities of the multi-degree-of-freedom, non-orthogonal effector configuration that a human hand in fact is. In this view, movements intended to take place in the XY plane are accompanied by inadvertent force variations along the Z-axis because the system is not exhibiting ideal active or passive compliance or both. If the system is geared to high stiffness, force variations will be of high amplitude; if the system is highly compliant, force variations will be reduced. However, in any case, the result will be a strong coupling between pen-tip kinematics and pen-force variations. As Figure 1 shows, the writing hand is a polyarticular system consisting of a closed kinematic chain. It is polyarticular in the sense that each tendon spans a considerable number of joints, going from its muscular attachment in the forearm to the distal finger tip. A grossly simplified biomechanical model describes APF as the consequence of compressing a viscoelastic system by moving the surface contact point in the direction of the normal at a fixed hinge. It also shows that in such a system, pen angle is directly related to pen tip position. Empirical evidence (1 subject) for the latter point is found in Deinet et al. (1987).
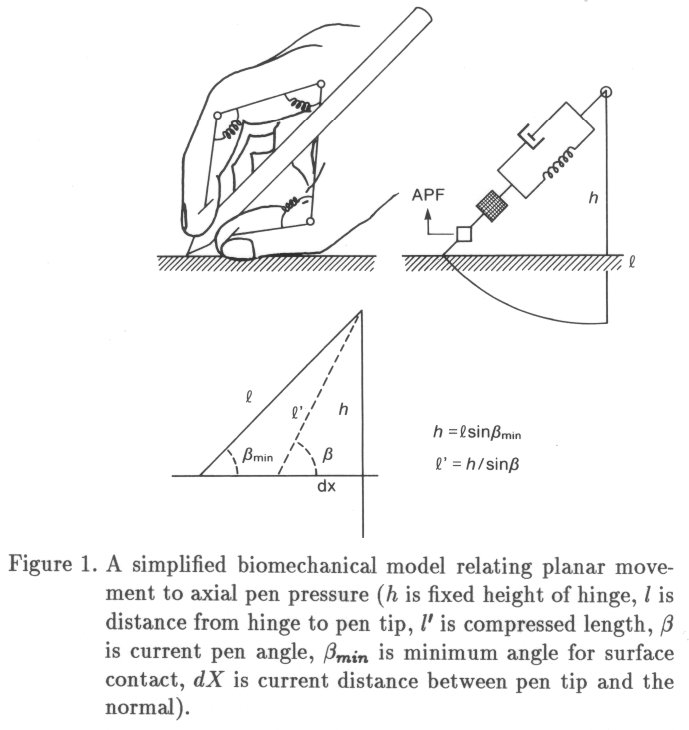
For example, in the pen-grip style with the palmar part of the wrist resting virtually flat on the writing surface, the finger flexion and extension will lead to larger variations in pen angle than wrist adduction and abduction, as an observation of the rear end of the pen during simple linear writing movements will reveal. The biomechanical hypothesis is attractive from the point of view of control efficiency. An appealing theory on skeleto-muscular motor control states that movements are brought about by the planning of muscle length ratios at target positions (Bizzi, Polit & Morasso, 1976; Morasso & Mussa Ivaldi, 1987; Hogan, 1985). In this view, movement is an equilibrium trajectory of minimum potential energy caused by the elastic energy that is stored by muscular (co-)contraction. This type of control obliterates a temporally fine-grained trajectory planning between intermediate target positions. Similarly, the application of force to external objects is the direct result of the difference between the stored elastic energy state and the state the motor system is forced to maintain after obstruction by an external object. In handwriting, the obstruction is presented by the pen, yielding pen-grip force, and by the writing surface, yielding NPF and friction. In equilibrium theory, the planned virtual trajectory would be located spatially beneath the writing surface. If we assume that the elastic energy potential function Ep of the end effector is smooth (a valley), that the movement direction coincides with the major or minor stiffness axis (Hogan, 1985), and that the movement does not cross the equilibrium point, there is a linear relation between small displacements and force. Under the same assumptions, force will generally covary strongly with displacement in complex movements patterns, too, since Ep is monotonically increasing with distance from the equilibrium point. The exception is the special case of the isotonic trajectories in which the shape of the movement pattern is fully determined by a constant force constraint.
However, it can also be hypothesized that variations in pen force are actively regulated by a central nervous system (CNS) process, independent of the trajectory control. For example, Kao et al. (1983) found an increase in normal pen force (NPF) as the patterns to be copied became increasingly complex. Another finding of this study was that pen force increased during the production of a single pattern. Furthermore, there is are many older (German) studies, relating pen force to high-level constructs such as personality or mental state (Kraepelin, 1899; Kretschmer, 1934; Steinwachs, 1969). A problem with these latter theories is that they do not attempt to describe important physical aspects of the pen-force control problem.
Leaving aside hypotheses that attach weight to high-level constructs, such as, e.g., mental stress, as causing the pen-force variations (Steinwachs, 1969), it can be hypothesized that in the process of learning to write the letter shapes (allographs), the writer adopts his own strategy or style of controlling pen force during trajectory formation. According to this viewpoint, the main intention of the movements is to produce spatial shapes within a certain amount of time. The shape of the pen-force time function would be only indirectly of importance: its average level should be just high enough to produce a trace of sufficient thickness. If force variations are indeed purely a matter of personal writing style, the result would be a complex, subject-dependent relation between pen tip kinematics and pen force.
The question of whether pen force is a natural, physical consequence of finger movement or an independently controlled variable is especially important in models of handwriting. Plamondon and Maarse (1989) give an overview of 14 models of handwriting from the point of view of systems theory. These models are two-dimensional and do not incorporate pen-force or mechanical impedance control. Ideally, to be included in these models, the pen-force signal should be independent of the movement control signals. Also, before developing a coupled oscillator model (Beek & Beek, 1988) of pen-force control, one must know if there is any coupling at all.
Although the separation of passive from active aspects in the handwriting process is a very complicated problem, and probably only partly solvable because the nervous system makes efficient use of the biomechanical and physiological characteristics of the effector and sensor systems in an integrated fashion, it seems worthwhile to test to what extent pen force is related to movement.
In a pilot study on the handwriting and drawing movements of two subjects, two methods of analysis were performed to test the relation between movement and pen force. First, it was argued that a simple first-order correlation would not suffice because of phase or time differences between the movement (displacement, velocity, acceleration and angular velocity) and the force signal. Therefore, a cross-correlation analysis was performed. Results revealed that the cross-correlation never displayed a consistent and reproducible clear peak value above 0.8 at a fixed delay, and correlation values were lowest if the movements involved scribbles or cursive handwriting. Subsequently, a second type of analysis was performed, that was based on the assumption that the combined linear contribution of planar displacement, velocity and acceleration yielded, by biomechanical coupling, an axial component of pen force. The latter analysis (linear multiple regression) did not yield consistent results in terms of signal significance or the proportion of explained variance. The conclusions of the pilot experiment were threefold. First, it appeared that it was of essential importance to control the pen-grip style of the subjects in order to allow for a comparison of finger and wrist contributions to the movement. For example, short straight lines of length 1 cm at an angle of 45 degrees can be produced by the wrist, the fingers, or a combination of both, depending on the forearm attitude. Second, it was evident that, in order to rule out either the "biomechanical" or the "central" explanation for pen-force variations, a larger number of subjects and recordings was necessary. Third, it can be argued that the lack of consistent findings is caused by the fact that the relation between movement and force is only significant within a limited frequency band, e.g., the 5 Hz periodicity in handwriting (Teulings & Maarse, 1984; Maarse, Schomaker & Thomassen, 1986), and that a lumped correlation measure hides such a dependency.
It is hypothesized that if pen force is the direct consequence of biomechanical loading and unloading of the wrist and finger muscles, it should covary with the movement produced by the stroke production process, regardless of the complexity of the drawing pattern as a whole, e.g., pen force invariably going up in downward strokes. In one study the fingers are mentioned as having a larger effect on pen-force variation than wrist movement (Dooijes, 1984).
According to several handwriting models, writing movements are generated by a system that produces bell-shaped tangential velocity profiles (ßtrokes") of the effector (Morasso & Mussa Ivaldi, 1982), along with the production of bell-shaped angular velocity profiles (Plamondon, 1987; 1989). A possible coupling (synergism) between this (CNS) stroke production mechanism and the pen pressure should be revealed by high coherence between tangential velocity and/or angular velocity on the one hand, and APF on the other hand. In this case, a hypothesis that can be put forward is that pen force will be increased at stroke transitions, where the tangential velocity is low and the angular velocity and curvature are high. We use the term tangential velocity instead of the more general term curvilinear velocity because we are dealing with planar movement.
In order to determine the existence and strength of linear relationships between movement and axial pen force, we will calculate the coherence spectrum for several types of handwriting patterns. The Cartesian displacement coordinates will be transformed into an estimate of the oblique system that represents the directions of wrist and finger movement, respectively. This provides the opportunity to separate the wrist and finger contributions to the axial pen force. Also, the coherence between APF and tangential velocity as well as angular velocity will be determined. A set of drawing patterns will be used, varying in complexity from straight lines to scribbles and cursive script.
2 Methods
Subjects. Sixteen right-handed students, five male and
eleven female, with an average age of 23.3 years, participated
in the experiment. Subjects were not informed of the purpose
of the experiment (i.e. that "pen pressure" was being measured).
Materials. The movements of the tip of the writing stylus
were recorded by means of a large-size writing tablet (Calcomp
9000). The sampling frequency was 105.2 Hz, samples having a
resolution of 0.025 mm and an accuracy of 0.25 mm in both X and Y directions.
The tablet was connected to a PDP 11/45 computer via a 9600 baud serial
line. The laboratory-made writing stylus was equipped with a strain-gauge force
transducer, measuring axial pen force in the 0-10 N range. The stylus contained
a normal ball-point refill in tight contact with the force transducer.
The analog signal from the pen-force transducer was low-pass
filtered (second-order Butterworth, -3dB at 17.5 Hz) and A/D
converted with a resolution of 10 bits. Data were stored on
magnetic tape and copied to a VAXstation 2000 computer where the
actual analyses were done. Software was written in Fortran-77.
Procedure. The subjects' task was to write predefined patterns or cursive words on a DIN A4 paper sheet placed on the writing tablet. The tablet was placed in such a way that the subject was sitting in a convenient position, writing at a preferred angle, just as in a normal writing situation. Patterns had to be written at a pace corresponding to normal writing speed. The recording of a single drawing pattern lasted 12 seconds. The duration of the writing of a single word is writer-dependent, but the maximum duration was set at 12 seconds. Before the actual recording took place, subjects had the opportunity to accustom themselves to the experimental set-up and to the writing patterns that were te be used. The writing patterns were practised three times each. To eliminate arm movements, the forearm was placed and fixed in an adjustable special-purpose cuff attached to the digitizer (Maarse, Schomaker, & Thomassen, 1986). The forearm was fixed in such a way that its inner side was parallel to the vertical axis (Y) of the digitizer. In order to allow free movement of the hand, the ulnar side of the processus styloideus ulnae was just above the top edge of the cuff (Figure 2).
Writing patterns were indicated by simple icons on the response sheet (Figure 3), on which six patterns were randomly distributed, and amounted to ten trials per pattern. The following writing patterns were used. In condition "F" (fingers), the subject had to make an oscillating writing movement at a preferred frequency, producing a short (maximally 6 mm) straight line by moving the fingers only, holding the wrist still, in a relaxed attitude. In condition "W" (wrist), the subject was asked to perform similar writing movements, in this case producing a straight line by using the wrist only, and holding the fingers still in a relaxed attitude. In a third condition, "C-", the subject had to draw counter-clockwise circles, about 5 to 6 mm in diameter. In a similar fourth condition, "C+", the circles were drawn in a clockwise fashion. In the fifth condition, "S", the subject had to draw scribbles, aiming at a spatial range of 6 by 6 millimeters, maximally. In the sixth condition,"H" (handwriting), the subject had to write the Dutch word "gestaakt" (ßtruck") in cursive style, without pen-lifts. This word was selected because it contains body-sized letters as well as ascenders and descenders, and is not too long. Care was taken to optimize the dynamic range of the wrist and finger movements, since the forearm was fixed. The subject was instructed to hold the writing hand relaxed in its preferred position. Finally, the response sheet was positioned with the left hand until the pen tip pointed to the center of the white response area below the stimulus pattern. No pen lifting was allowed during the trials.
Per subject, a data set of 10 trials x 6 patterns x 1280 samples x 3 coordinates (X,Y,APF) was collected (460.8 kilobytes). From each trial in the drawing pattern conditions, the middle 1024 samples (9.733s) were used in the analyses, thereby removing possible artefacts appearing during the initial and final periods of 128 samples (0.122s) at the beginning and at the end of a trial. From each trial in the text condition, the middle 256 samples (2.433s) of the written word were used (average word duration was 4.9 seconds). The signals, horizontal displacement (Sx), and vertical displacement (Sy), were obliquely transformed (Dooijes, 1984), using:
| ||||||||||||||||||||||||||||||||||||||
(2)
where l is the estimated angle for the axis of the wrist system, with respect to the Cartesian x-axis, and m is the estimated angle of the axis of the finger system with respect to the Cartesian x-axis. The angle f represents the angle between the wrist and finger axes. The wrist axis angle is obtained by estimating the angle of the written line from the (Sx ,Sy) coordinates in the "W" trials of a subject by linear regression. The finger axis angle is obtained by estimating the angle of the written line from the (Sx,Sy) coordinates in the "F" trials of a subject by linear regression. The application of eq. (2) transforms the data to the estimated ïnternal" effector coordinate system, with wrist activity indicated by Sw, and finger activity indicated by Sf.
The displacement signals Sx, Sy, wrist activity (Sw), finger activity (Sf), and axial pen force (APF), were differentiated, using a five-point convolution window with Lagrange weights (1/12, -8/12, 0, 8/12 and -1/12, Abramowitz & Stegun, 1970). The frequency domain transfer function of this differentiator is linear up to about 13 Hz in our case. Thus, the signals Vx,Vy, wrist velocity (Vw), finger velocity (Vf) and differentiated APF (i.e., dAPF) were obtained. From Vx and Vy, the tangential velocity (Va) and angular velocity (Vq) were calculated. The reason for the time-domain differentiation is twofold: (a) it removes low-frequency variations that would lead to large bias errors in the low-frequency range of the Fourier transform to be performed later, and (b) it keeps spectral components in the frequency range of interest (3-13 Hz) intact. Differentiation has virtually no effect on the coherence function estimate (see Appendix). Of each signal, the Fast Fourier Transform (FFT) was calculated per trial per condition per subject, after tapering with a 10 percent cosine window (Bendat & Piersol, 1971; van Boxtel & Schomaker, 1983). Bandwidth resolution (Br) before smoothing was 0.103 Hz except in the case of the handwriting condition where Br was equal to 0.411 Hz. The Fourier spectrum was transformed to a power spectral density function (PSDF). Also, cross power spectral density functions (CSDF) were calculated for the following comparisons: dAPF vs wrist velocity Vw, dAPF vs finger velocity Vf, dAPF vs tangential velocity Va, and, finally, dAPF vs angular velocity (Vq), a signal closely related to curvature.
The PSDF and CSDF were then smoothed with a rectangular window (l = 5) in order to increase the reliability of the individual spectral estimates and to make it possible to calculate the spectral coherence function (Bendat & Piersol, 1971). Then, per subject, per condition, the PSDF and CSDF spectra were averaged over the ten trials in a condition to obtain ensemble averages. This yields 2x5x10=100 statistical degrees of freedom for the average smoothed PSDF and CSDF per subject per condition. To obtain a general estimate of the PSDFs and coherence functions per condition, however, the ensemble average spectra were again averaged over the sixteen subjects. The PSDFs were normalized to unit area before averaging, and the obtained condition average was rescaled to physical units again. A condition average PSDF has 16x100=1600 statistical degrees of freedom. The coherence functions underwent Fisher's Z transform before averaging, the average being converted to the coherence domain again. The squared coherence (also called Magnitude Squared Coherence or MSC) is given by:
|
(3)
where:
| ||||||||||||||||||||||||
In order to test for non-stationarity, run tests were performed on all signals of each trial. The runs were determined by dividing each sample record into 10 segments of equal duration and calculating the 10 mean square values and their median value. This procedures captures non-stationarities in the mean and the variance of the signal. It is assumed that data are (weakly) stationary if maximally 5% of the trials exhibit a number of runs that has a probability of less than 0.05 of originating from a random process.
3 Results
The run tests revealed the following percentages (N=960) of sample records yielding a number of runs with p < .05: dAPF 3.23%, Vw 2.08%, Vf 3.02%, Vq 3.33%, all below 5%. There was no systematic relation between number of runs and condition. Table 1 shows the results for the preferred angles of the lines drawn in the conditions W and F. From the mean difference value, it can be inferred that the wrist and finger systems have approximately orthogonal movement axes, given the forearm attitude used.
Table 1.
Average preferred angles in degrees for the linear wrist and finger
movements with respect to the X-axis of the digitizer,
and their difference. Note that the forearm is aligned with the
Y-axis of the digitizer.
Subject Wrist Fingers F-W
01 36 136 100
02 26 132 106
03 44 127 83
04 35 129 95
05 36 127 91
06 36 141 105
07 52 136 85
08 35 134 98
09 48 128 79
10 31 146 115
11 22 132 110
12 39 130 91
13 39 127 88
14 42 123 81
15 53 159 106
16 48 134 86
Mean 39 134 95

Figure 4 shows a superposition of the patterns produced by wrist movement and by finger movement in a trial of the W and F conditions, respectively. The widths of the patterns indicate that the wrist movements are more accurate than the finger movements, a finding consistent with earlier studies (Maarse, Schomaker & Thomassen, 1986). Figure 5 shows the dAPF and Vf signals of a single trial in the clockwise circling (C+) condition, a time segment of 1s within this trial and the shape of both the total circling pattern and the selected 1s segment.
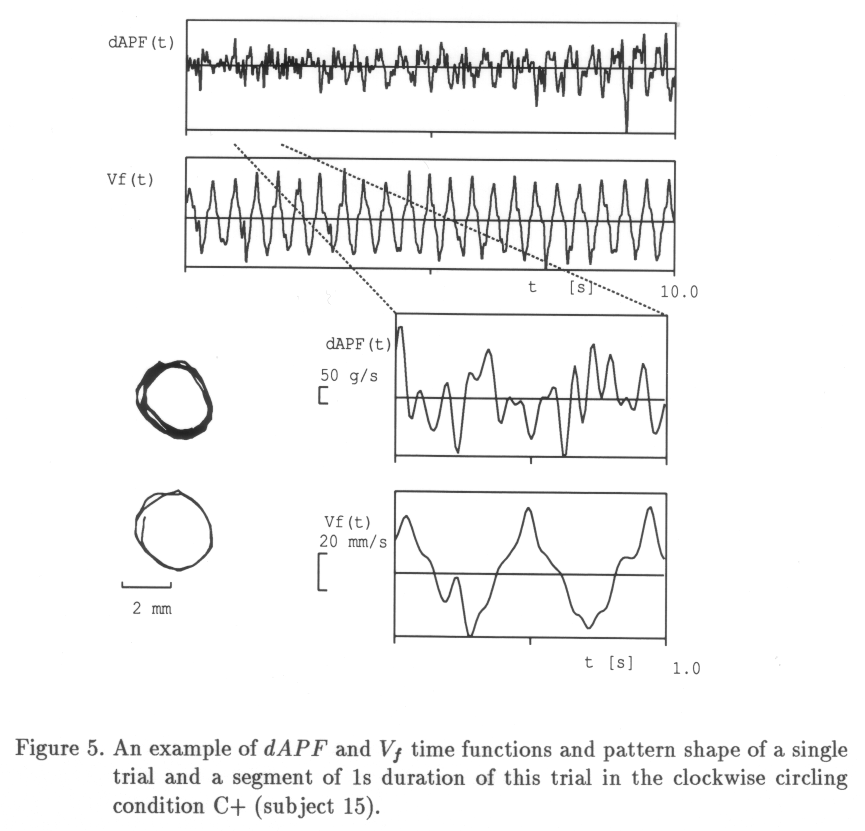
Figures 6 and 7 show the results of the comparisons of dAPF with Vw andVf (wrist and finger domain velocities). The figures are scaled in physical units to enable comparison. The smoothness of the handwriting spectra (panel H) as compared to the simple drawing spectra (panels C+,C-,F,W,S) is due to the shorter sample record duration in the former, resulting in a lower spectral resolution.
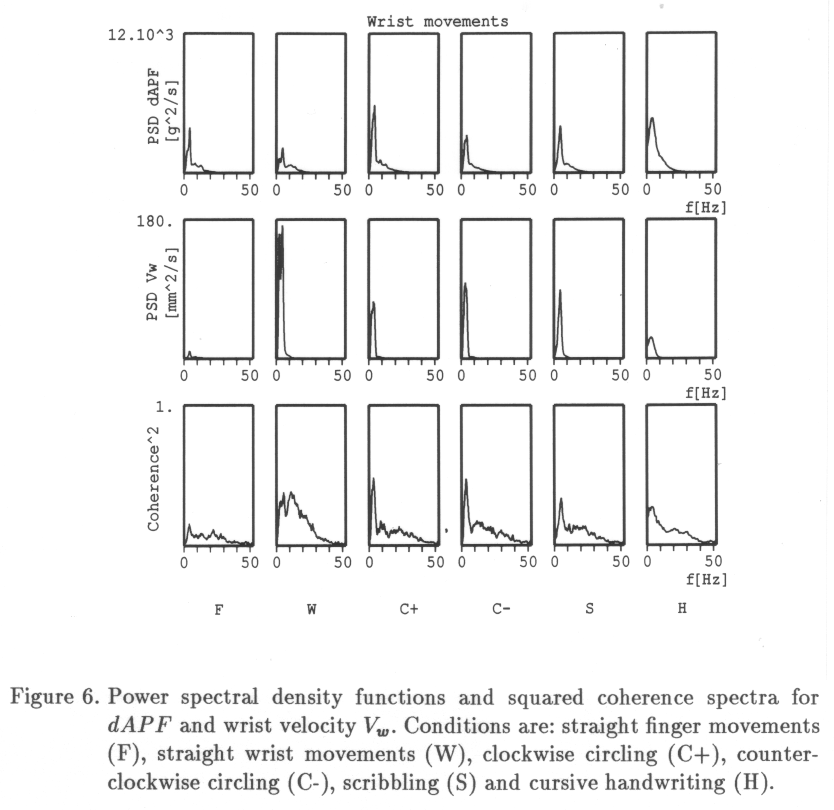

From the figures it is clear that all PSDFs (dAPF and kinematics) have a peak in the area of two to five Hz. The peak in the dAPF spectrum occurs at about the same frequency as the peak in the kinematics spectra, small deviations being due to the estimation error. The main difference between the dAPF and kinematics spectra is the relatively larger amount of dAPF power in the range above eight Hz, for all conditions. The most probable explanation is the contribution of friction with its hysteresis effects, and the paper surface irregularities in the APF signal. In fact, hysteresis could be inferred clearly in the single-subject dAPF PSDFs of six of the sixteen subjects, showing peaks up to the second harmonic. The reduced remainders of these higher harmonics can be seen in the average dAPF PSDF of the clockwise circling (panel C+) and the finger movement (panel F) conditions. Overall dAPF power is greatest in handwriting (panel H), intermediate in scribbles (panel S) and circling (panels C+,C-), and small in straight finger and wrist movements (panels F and W). The average, variance and time trend of the primitive APF signal are shown in Table 2. The average APF is not related to variance in this series of conditions. In cursive script, there is a positive time trend, in the other conditions, APF decreases slowly during a trial.
Table 2.
Average APF measures for all conditions, in [g] unless
otherwise stated. Note the maximum variance and positive
time trend in the cursive script condition (H). APF(0) and
APF(n) denote linearly estimated initial and final force level,
b is the gain of the time trend, r is correlation of APF vs time.
m s2 (g2) APF0 APFn b (g/s)
r ()
S 83.6 284.5 91.3 75.9 -2 -0.27
W 87.5 250.6 95.0 80.1 -1 -0.29
C+ 108.9 295.9 116.0 101.8 -1 -0.25
H 109.7 806.4 91.6 127.7 +8 +0.39
F 113.5 259.2 121.2 105.8 -1 -0.26
C- 115.3 307.7 124.0 106.6 -2 -0.29
The kinematics PSDFs in circling and scribbling are roughly comparable in shape and area (Figures 6 and 7, panels C+, C- and S). The differences in peak power values between circling and scribbling spectra reflect differences in spatial movement amplitude, rather than differences in periodicity, as can be inferred from peak width. When subjects are asked to produce scribbles, the temporal behavior is thus not as irregular as the spatial result would lead one to suspect. Scribbling is performed faster (average peak frequency 4.5 Hz) than circling (3.5 Hz).
Furthermore, as could be expected, the power of movements along the finger axis is greatly reduced when wrist movements were requested (Figure 7, panel W). This suppression takes place to a lesser extent with respect to the power of movements along the wrist axis in case of finger movements (Figure 6, panel F).
In the comparison between dAPF and the wrist velocity Vw, it appears that a maximum peak coherence (0.42 to 0.44) is reached in circling movements (Figure 6, panels C+ and C-). The difference in peak coherence between clockwise and counter-clockwise circling is small. This means that maximally 40% of the power in dAPF at the fundamental movement frequency can be explained by wrist movements, if the movements are circular. In straight wrist movements (W), the peak coherence is somewhat lower (0.35) but the more striking feature is that coherence is smeared out over a broad band from 5 to 20 Hz, (Figure 6, panel W). In straight finger movements, the wrist contribution to dAPF is negligible. The shape of the coherence spectrum for the scribbling movements is comparable to that for circling, but the peak coherence is lower (0.3). In producing cursive handwriting (panel H), peak coherence is still lower (0.25) and the shape of the coherence spectrum is broad banded.
In the comparison between dAPF and the finger velocity, peak coherence values and coherence spectrum shape are similar to those in the dAPF-Vw comparison, with the exception of the straight finger movement condition. The finger velocity in straight finger movements (Figure 7, panel F) explains 0.49 of the dAPF power at the fundamental oscillation frequency, which is the maximum peak coherence value obtained in this study. The coherence spectrum shape is of the broad-band type with peaks at the fundamental frequency 4.5 Hz, at 13.0 Hz and at 21.7 Hz. The coherence between the wrist velocity and dAPF is very low in straight finger movements (0.14).
The coherence between dAPF and tangential velocity or between dAPF and angular velocity Vq never reached a value above 0.3 in any condition.
An analysis of variance on the Z-transformed first-order (Pearson) correlation between APF and Sw and between APF and Sf revealed the significant main effects Condition (p < .0001, 5 df), Effector (i.e., Wrist vs Fingers) (p < .0001, 1 df), Subject (p < .0001, 15 df). The interactions were: a trivial Effector*Condition (p < .0001, 5 df) due to the F and W conditions, Subject*Effector (p < .0001, 15 df), Subject*Condition (p < .0001, 75 df). The finger movements were slightly more strongly correlated to APF (mean r=-0.23) than the wrist movements (mean r=-0.14). Note that in this analysis the sign of the correlation biases the average, unlike the case of mean coherence values. There is only one positive correlation (+0.09), between APF and finger displacement in the W condition. The correlation figures should be squared for comparison with coherence values. The largest mean correlation found was -0.39 for the fingers in the clockwise circling condition (C+). Clockwise circling (C+) yielded higher correlation values than counter-clockwise circling (C-) (Table 3).
Table 3.
Average first-order (Pearson) correlations over subjects (N=16)
between APF and finger displacement Sf and between APF and
wrist displacement Sw for all conditions.
Condition: F W C+ C- S H Mean
Effector:
R(APF,Sf) (Fingers) -0.36 0.09 -0.39 -0.24 -0.20 -0.22 -0.23
R(APF,Sw) (Wrist) -0.02 -0.15 -0.33 -0.11 -0.14 -0.10 -0.14
Mean -0.20 -0.03 -0.36 -0.17 -0.17 -0.16
To exclude the possible influence of pen angle variation, and consequent variation in the pen force, a test was performed with a modified tablet controller from which pen angle could be derived with an accuracy of 3 degrees (Maarse, Janssen & Dexel, 1988). The controller device was only available after collection of the main data set. Recordings (T=9 s) never revealed correlations below 0.96 between axial and normal pen force in any of the conditions (N=4 subjects). The reason for this strong relationship is the small amplitude of the pen angle variations (2.5 degrees) with respect to the average value (50 degrees).
Results thus far seem to indicate that, in cursive script, the relation between pen force and kinematics is rather weak, and that only in simple movement patterns a coherence of intermediate value can be observed. However, from a visual analysis of the single-subject time records, the impression was that the correlation between APF and kinematics is actually waxing and waning in time. We will now proceed to analyze this behavior for the cursive script condition (H). In order to determine the development of the relation between APF and vertical displacement over time, an instantaneous (running) Pearson r (rAPF,Y51(t)) (see Appendix) was calculated, using a window width of 51 samples, corresponding to about half a second, or at least a number of five strokes. This window-width value is not critical, as long as it is large enough to contain several strokes, and small enough to fluctuate within the sample record (the written word "gestaakt"). For simplicity, the raw vertical displacement Y(t) was chosen. This signal contains a large proportion of finger movement (Table 1). It appears that roughly three types of subjects were present.
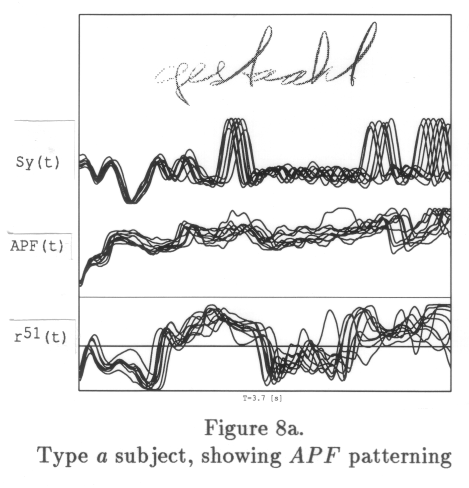

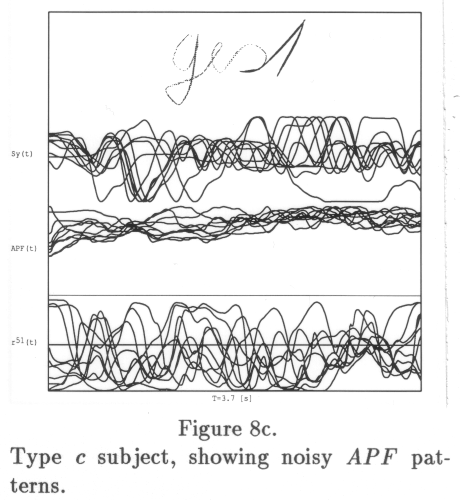
| Figure 8. Instantaneous Pearson r51 between APF and vertical displacement Sy during the production of a cursive word in three types of subjects. The relative APF level is coded in grey scale (high force in black). |
Type a subjects (10 in 16) show a high number of sign reversals ( > 4)
of the correlation rAPF,Y51(t) (Figure 8a). Locally, however, absolute
correlation values of 0.8 in rAPF,Y51(t) were not uncommon. Overall
correlation (and coherence) was low. Especially interesting in type a
subjects is the fact that the shape of APF(t), Y(t) and the correlation
time function rAPF,Y51(t) were well replicated over trials in the
cursive script condition.
Type b subjects (2 in 16) show a much more smooth pattern
of rAPF,Y51(t), with a limited number of brief sign
reversals, and a relatively high but negative correlation value (Figure 8b).
There is a medium inter-trial consistency.
Type c subjects (4 in 16) show noisy displacement and APF patterns and a consequently low correlation with kinematics (Figure 8c).
In order to track down the origin of the fluctuations in rAPF,Y51(t), a measure of replicatability of both APF(t) and Y(t) was needed. We chose to calculate the average correlations, via Fisher's Z transform, between replications of a word for APF, yielding RAPF,APF, and for the vertical displacement, yielding RY,Y. These measures will indicate the degree to which the writer was able to replicate the APF or Sy patterns over different realizations of the written word, given the beginning of the first down stroke in as the time synchronization reference. For comparison, the within-trial average correlation between APF and vertical displacement, RAPF,Y, was also calculated. The next measure calculated was the number of runs or phases, Nphases, in rAPF,Y51(t), in order to provide a measure of the complexity of the relation between APF(t) and Y(t).
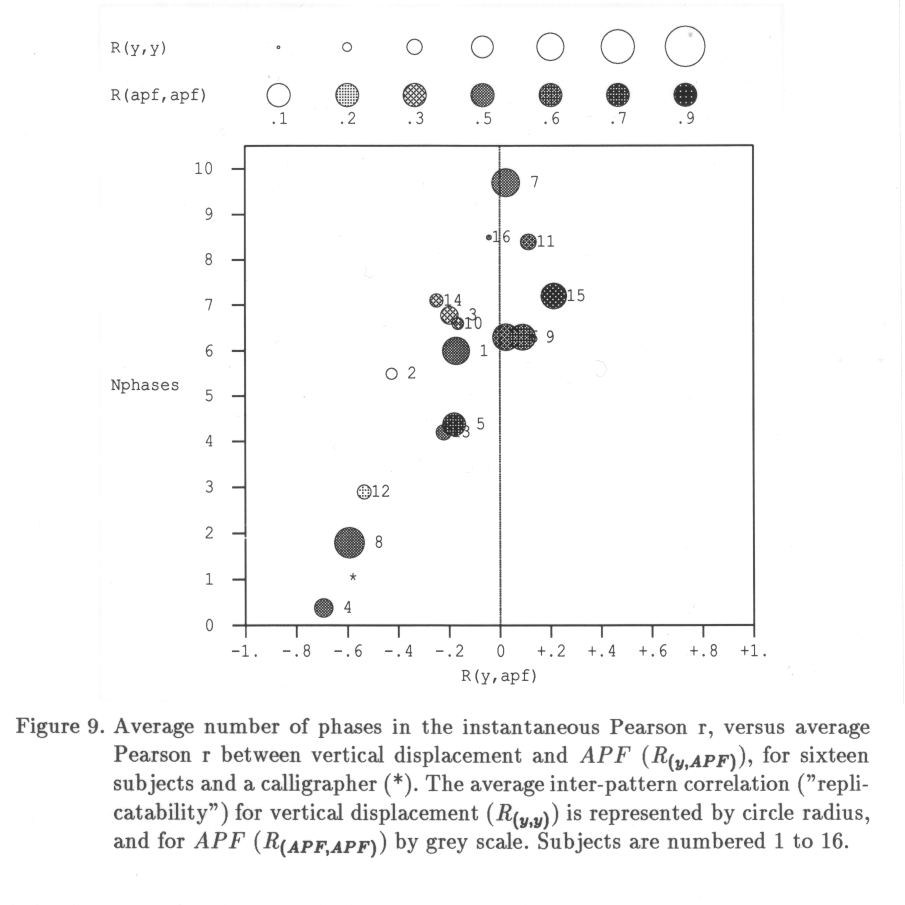
Figure 9 shows the distribution of subjects in a two-dimensional space of correlation complexity (Nphases) versus the average correlation between vertical displacement and APF (RAPF,Y). The replicatability of the APF and vertical displacement pattern Sy, as reflected in average inter-pattern correlations also are shown (RAPF,APF and RY,Y). Typical type a subjects are numbers seven and fifteen, typical type b subjects are numbers four and eight. Subjects two, ten, twelve and sixteen are typical of the type c category: note the small radius and light shading that are indicative of low inter-trial replicatability for both vertical displacement and APF for these subjects. Interestingly, from recordings of a calligrapher it was found that this person can be classified as a type b subject, as indicated by an asterisk (Figure 9). Table 4 contains the within and between-pattern correlations for all subjects, for the whole word "gestaakt" (4a) and for the time segment that corresponds to the first letter (4b). This letter was selected because it did not display allographic variation over the subjects. All subjects wrote it much in the same way, such that a clean ensemble average over 160 replications could be obtained (Schomaker & Thomassen, 1986). As could be expected from the rAPF,Y51(t) fluctuations, locally, within the , a somewhat stronger relation between APF and Sy can be found: another two subjects display a value of RAPF,Y that is less than -0.6. Subjects six, ten and sixteen display elevated writing times. Trend removal from APF and Sy yielded very similar figures. Figure 10 shows the time-normalized ensemble averages (n=10) of per subject and the overall average (n=160). Apart from the time normalization, no DC or amplitude normalization was performed in the calculation of the averages, but because of between-subject differences in the average APF level, Figure 10 is scaled to fit optimally, assuming an APF origin of 0. The panels are sorted in an order of increased relative APF variance, with the result that subjects with a low absolute correlation between APF and Sy are predominant in the top row, with an approximately flat APF profile, and subjects with a higher (negative) correlation between APF and Sy are predominant in the bottom row. Note the different APF patterns for each subject.

Table 4.
Average correlations (N=10 replications) between APF
and Sy, between the Sy functions of different replications
and between APF functions of different replications of the word
"gestaakt" (4a) and its first letter (4b), for all
subjects. Also shown are the average APF level and its
standard deviation and the average writing time.
4a. The word "gestaakt".
Subject R(APF,Y) R(Y,Y) R(APF,APF) mAPF sAPF T
(g) (g) (s)
01 -0.17 0.60 0.43 57 18 3.419
02 -0.43 0.24 0.11 60 12 2.974
03 -0.20 0.38 0.32 128 16 4.917
04 -0.70 0.39 0.47 85 18 4.312
05 -0.18 0.50 0.73 212 25 3.592
06 0.02 0.57 0.55 65 14 10.133
07 0.02 0.61 0.43 95 11 3.319
08 -0.59 0.65 0.45 100 25 2.596
09 0.09 0.57 0.65 114 25 3.361
10 -0.17 0.25 0.40 175 24 8.663
11 0.11 0.35 0.55 66 23 3.761
12 -0.54 0.31 0.14 83 19 5.990
13 -0.22 0.34 0.47 58 11 3.564
14 -0.25 0.29 0.36 97 15 5.471
15 0.21 0.56 0.77 140 19 3.736
16 -0.04 0.11 0.41 114 17 8.107
4b. First in "gestaakt".
Subject R(APF,Y) R(Y,Y) R(APF,APF) mAPF sAPF T
(g) (g) (s)
01 -0.19 0.52 0.43 154 7 0.278
02 -0.04 0.64 0.54 146 7 0.236
03 -0.21 0.76 0.60 88 8 0.373
04 -0.72 0.79 0.57 83 6 0.309
05 -0.60 0.53 0.36 67 20 0.287
06 0.28 0.79 -0.01 105 9 0.796
07 -0.12 0.76 0.46 226 28 0.247
08 -0.61 0.84 0.81 125 11 0.215
09 -0.41 0.67 0.48 72 17 0.328
10 -0.10 0.78 0.75 100 5 0.462
11 -0.25 0.71 0.31 74 5 0.279
12 -0.46 0.33 0.46 210 13 0.542
13 -0.60 0.64 0.62 89 11 0.326
14 0.01 0.83 0.66 130 16 0.419
15 0.19 0.77 0.67 57 6 0.309
16 0.00 0.49 0.01 93 19 0.694
4 Discussion
The moderate coherence values obtained indicate that, at least for the majority of writers, a simple biomechanical coupling between APF and kinematics is unlikely. The residual non-ideal or non-linear relation that exists, attains its greatest strength in simple linear movements, with low average pressure levels, deteriorating as movement complexity increases. Since the periodicity of the axial pen-force variations is the same as the periodicity of the movements, it must be the phase relation between the two that is time-variant or noisy. This latter explanation is supported by the finding that the first-order correlation between pen force and displacement fluctuates over time. The pen angle can be discarded as a cause of this phase jitter because it is coupled to the pen tip kinematics. With regard to pure spatial factors, like points of high curvature, the data reveal that there is no coherence between APF and tangential velocity or angular velocity. Since points of low velocity and high angular velocity correspond to the high-curvature points, high-order inter-relationships of this kind can be excluded. On the whole, pen force appears to be a separate control variable.
The mean first-order correlation over the subjects, between APF and wrist displacement, and between APF and finger displacement, shows comparable results to the coherence analysis but the values are lower, supporting the hypothesis that residual biomechanical coupling takes place predominantly at the modal movement frequency. There are indications that the residual correlations are due to biomechanical effects. The sign of these correlations is mostly negative, relatively higher APF corresponding to finger flexion and wrist radial abduction. On the whole however, variance in APF cannot be explained by kinematic variables. The fact that APF is somewhat stronger coupled (Table 3.) with movement in the clockwise circling condition than it is in counter-clockwise circling could be explained by the existence of a curl term in the stiffness matrix (Hogan, 1985) that has to be overruled in clockwise movement. More specifically, this finding points to a larger stiffness of the thumb subsystem as compared to the opposing finger system. For the cursive script condition, a more detailed analysis revealed three categories of subjects. Type a subjects ("APF patterners") displayed a complex but replicatable relationship between APF and displacement. The replicatability of the pen-force pattern and the instantaneous force-displacement correlation pattern both support the notion of independent, feedforward control of the force by the CNS in many subjects. It is well known that in handwriting at least one, but most probably several, strokes are planned in advance (Hulstijn & van Galen, 1983; Stelmach & Teulings, 1983). Transmission delays exclude the possibility of a continuously monitored pen tip displacement in a neural feedback loop. The average observed writing speed is eight to twelve strokes per second in the adult cursive writer. In type a subjects, it is quite likely that CNS advance planning or feedforward control is also the case with the pen force aspects (average force level and impedance) of the writing movement as it is with the trajectory formation (Rack, 1981).
In a small minority of subjects (type b, "biomechanics"), there can be a strong coupling between axial pen force and movement kinematics. The sign of the correlation between vertical displacement and APF is negative, which means that APF does indeed increase in down strokes (Dooijes, 1984), at least in this group of writers.
A third group of subjects is characterized by low replicatability of both kinematics as well as APF (type c, ßhakers"). It is as if these writers do not have a stable internal representation for cursive script movements.
In the current experiment, most subjects fall into category a. Here, the correlation between the force and displacement is time-variant, biphasic, and subject-dependent. The writer's strategy might be, at some time or in some specific writing context, to actively pre-program mechanical impedance during movement, thereby minimizing pen-force variations. This can be achieved by an anticipatory lowering of the amount of agonist/antagonist co-contraction. If the writer overcompensates, the sign of the resulting force-displacement correlation will be the inverse of the sign of the correlation in the case of uncompensated biomechanical force variations. If the writer fails to compensate or even increases stiffness, e.g., if the trajectory formation control temporarily requires more resources, the force-displacement correlation will be determined by the amount of noise in the neuro-muscular force control and by the biomechanics. In human handwriting, it is unlikely that the stiffness regulation mechanism is Cartesian, plane-oriented such as is used in the robotical seam welding of curved surfaces. If a planar target trajectory requires a high degree of hand stiffness along the X and Y axes for positional accuracy, this generally will have a strong effect on the stiffness along the Z axis, too. Considering the effects of pen-to-paper friction, current findings show that in using the relatively low-friction ball point stylus, the friction influence on APF is nearly constant, as witnessed by the high correlation between APF and NPF. Dooijes (1984) estimates the friction to be about 4% of the NPF value in the 0-2 N range. However, more study is needed on this topic.
Conclusions.
The levels of the coherence and first-order correlation between pen force and pen-tip kinematics in drawing simple patterns and in cursive script are rather low for a majority of writers. However, the replicatability of the pen-force pattern for a given word and the replicatability of the instantaneous correlation pattern between vertical displacement and pen force shows that the lack of overall coherence cannot be explained by an external source of random noise. A possible explanation is the presence of a separate control component that regulates pen force in an idiosyncratic fashion for each writer. One may speculate that this is possible since pen force is an extraneous, invisible variable, the time function of which is not explicitly addressed in the course of learning cursive script. The current findings are consistent with the known high discriminatory value of pen pressure in writer identification. A major implication for handwriting modeling (Hollerbach, 1981; Edelman & Flash, 1987; Schomaker, Thomassen & Teulings, 1989) is that trajectory control can be separated from pen-force control. The availability of a pen angle signal will allow for more detailed analyses, e.g., a decomposition of the axial pen force into 3-dimensional components. As a preliminary result however, it appears that pen angle variations are too small to explain a large proportion of the pen-force variance. The control of pen force during handwriting could be a paradigmatic example of how a biological manipulator handles mechanical impedance. Further studies will be needed on questions regarding the flexibility of the centrally controlled portion of pen force control in adapting to the various requirements of the motor task. This can be done by trying to teach the writer a given strategy of mechanical impedance control by means of artificial feedback about pen force. Such an experiment would reveal the learning ability of the human movement control system as compared to the teaching of the inverse dynamics solution to an artificial neural network (Kawato et al., 1987).
5 Appendix
1. The differentiation of two signals does not influence their coherence spectrum. Assume the signals u(t) and v(t), that are transformed by a linear operator h(t), then
| |||||||||||||
|
| |||||||||||||
2. The instantaneous or running Pearson correlation is given by:
|
|
Acknowledgements.
This study was supported by grants to Lambert Schomaker from
the Netherlands science organization NWO, project 560-259-020,
and from the European Esprit Programme, project 419.
This study was also supported by grants to Réjean Plamondon
from NSERC O915 and from The Netherlands Institute for
Advanced Study, 1989-1990.
Calligrapher's data courtesy of R.G.J. Meulenbroek.
6 References
Abramowitz, M., & Stegun, I.A. (1970). Handbook of mathematical functions (p. 914). Dover: New York.
Asada, H., & Slotine, J.-J.E. (1986). Robot analysis and control. New York: Wiley.
Baier, P.E., Teder, W., & Hussong, J. (1987). Future trends in automatic document analysis. In R. Plamondon, C.Y. Suen, J.-G. Deschênes, & G. Poulin (Eds.), Proceedings of the Third International Symposium on Handwriting and Computer Applications (pp. 146-151). Montreal: Ecole Polytechnique.
Bendat, J.S., & Piersol, A.G. (1971). Random data: Analysis and measurement procedures, London: Wiley.
Beek, P.J., & Beek, W.J. (1988). Tools for constructing dynamical models of rhythmic movement. Human Movement Science, 7, 301-342.
Bizzi, E., Polit, A., & Morasso, P. (1976). Mechanisms underlying achievement of final head position. Journal of Neurophysiology, 39, 435-444.
Crane,H.D., & Ostrem, J.S. (1983). Automatic Signature Verification Using a Three-Axis Force-Sensitive Pen, IEEE Transactions on Systems Man and Cybernetics, 13, 329-337.
Deinet, W., Linke, M., & Rieger, B. (1987). Analyse der Schreibdynamik. Technical Report, Bundeskriminalamt (BKA-Technische Forschung), Wiesbaden, February 1987, 278 pages.
Dooijes, E.H. (1984). Analysis of handwriting movements. Doctoral dissertation. Amsterdam: University of Amsterdam.
Edelman, S., & Flash, T. (1987). A model of handwriting Biological Cybernetics, 57, 25-36.
Hale, W.J., Paganini, B.J., (1980). An automatic personal verification system based on signature writing habits, Proceedings of the 1980 Carnahan Conference on Crime Countermeasures (pp. 121-125). Lexington: University of Kentucky.
Hogan, N. (1985). The mechanics of multi-joint posture and movement control. Biological Cybernetics, 52, 315-331.
Hollerbach, J.M. (1981). An oscillation theory of handwriting. Biological Cybernetics, 39, 139-156.
Hulstijn, W., & Van Galen, G.P. (1983). Programming in handwriting: Reaction time and movement time as a function of sequence length. Acta Psychologica, 54, 23-49.
Kao, H.S.R., Shek, D.T.L. and Lee, E.S.P. (1983). Control modes and task complexity in tracing and handwriting performance. Acta Psychologica, 54, 69-77.
Kawato, M., Furukawa, K., & Suzuki, R. (1987). A hierarchical neural network model for control and learning of voluntary movement. Biological Cybernetics, 57, 169-185.
Kobayashi, T. (1981). Some experimental studies on writing behavior. Hiroshima Forum for Psychology, 8, 27-38.
Kraepelin, E. (1899). Allgemeine Psychiatrie. Bd 2 (pp. 362-370). Leipzig: Thieme.
Kretschmer, E. (1934). A text-book of medical psychology (translated), (pp. 219-220). London: Milford, Oxford Univ. Press.
Maarse, F.J., Janssen, H.J.J., & Dexel, F. (1988). A special pen for an XY tablet. In F.J. Maarse, L.J.M. Mulder, W.P.B. Sjouw & A.E. Akkerman (Eds.), Computers in psychology: Methods, instrumentation, and psychodiagnostics (pp. 133-139). Amsterdam: Swets & Zeitlinger.
Maarse, F.J., Schomaker, L.R.B., & Teulings, H.-L. (1986). Kenmerkende verschillen in individueel schrijfgedrag: automatische identificatie van schrijvers. (Characteristic differences in individual writing behavior: Automatic writer identification), Nederlands Tijdschrift voor de Psychologie, 41, 41-47.
Maarse, F.J., Schomaker, L.R.B., & Teulings, H.L., (1988). Automatic identification of writers. In G.C. Van der Veer & G. Mulder (Eds.), Human-Computer Interaction: Psychonomic Aspects (pp. 353-360). New York: Springer.
Maarse, F.J., Schomaker, L.R.B., & Thomassen, A.J.W.M. (1986). The influence of changes in the effector coordinate system on handwriting movements. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 33-46). Amsterdam: North Holland.
Mason, M.T. (1982). Compliance and force control for computer controlled manipulators. In M. Brady, J.M. Hollerbach, T.L. Johnson, T. Lozano-Pérez & M.T. Mason (Eds.), Robot Motion: Planning and Control (pp. 373-404). Cambridge: MIT.
Morasso, P., & Mussa Ivaldi, F.A., (1982). Trajectory formation and handwriting: A computational model. Biological Cybernetics, 45, 131-142.
Morasso, P., & Mussa Ivaldi, F.A. (1987). Computational models of handwriting. In R. Plamondon, C.Y. Suen, J.-G. Deschênes, & G. Poulin (Eds.), Proceedings of the Third International Symposium on Handwriting and Computer Applications (pp. 8-9). Montreal: Ecole Polytechnique.
Plamondon, R. (1987). What does differential geometry tell us about handwriting generation? In R. Plamondon, C.Y. Suen, J.-G. Deschênes, & G. Poulin (Eds.), Proceedings of the Third International Symposium on Handwriting and Computer Applications, Montreal (pp. 25-27). Montreal: Ecole Polytechnique.
Plamondon, R., & Lorette, G. (1989). Automatic signature verification and writer identification: The state of the art. Pattern Recognition, 22, 107-131.
Plamondon, R., & Maarse, F.J. (1989). An evaluation of motor models of handwriting. IEEE Transactions on Systems, Man and Cybernetics, 19, 1060-1072.
Plamondon, R., (1989). Handwriting Control: A Functional Model. In R.M.J. Cotterill (Ed.), Models of Brain Function (pp. 563-574). Cambridge: University Press.
Rack, P.M.H. (1981). Limitations of somatosensory feedback in control of posture and movement. In V.B. Brooks, (Ed.). Handbook of physiology, section 1: The nervous system, Vol. 2: Motor control, part 1 (pp. 229-256). Bethesda: American Physiological Society.
Schomaker, L.R.B., & Thomassen, A.J.W.M. (1986). On the use and limitations of averaging handwriting signals. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 225-238). Amsterdam: North-Holland.
Schomaker, L.R.B., Thomassen, A.J.W.M., & Teulings, H.-L. (1989). A computational model of cursive handwriting. In R. Plamondon, C.Y. Suen, & M.L. Simner (Eds.), Computer Recognition and Human Production of Handwriting (pp. 153-177). Singapore: World Scientific.
Steinwachs, F. (1969). Mikromotorische Tonusregistrierungen und ihre diagnostische Moeglichkeiten. Jahrbuch, Landesamt fuer Forschung des Landes Nordrhein-Westfalen, Opladen (Germany): Westdeutscher Verlag.
Stelmach, G.E., & Teulings, H.-L. (1983). Response characteristics of prepared and restructured handwriting. Acta Psychologica, 54, 51-67.
Teulings, H.L., & Maarse, F.J. (1984). Digital recording and processing of handwriting movements. Human Movement Science, 3, 193-217.
Van Boxtel, A., & Schomaker, L.R.B. (1983). Motor unit firing rate during static contraction indicated by the surface EMG power spectrum. IEEE Transactions on Biomedical Engineering, 30, 601-609.
Chapter 5
Alternative approaches: Connectionism
As we have seen, the modeling approach used so far, has led to a modular symbolic processing architecture, specifying symbolic and quantitative data-structures and the operations performed on them. This approach is typical for the classical cognitivist viewpoint and is strongly related to methods used in artificial intelligence. The advantages of such an approach are the following:
- The resulting model is a working computer model, i.e., ideally it displays a functionality comparable to the human cognitive function that it is supposed to simulate.
- Basic processing steps are made explicit.
- In the process of model development, new and essential functionality that was previously implicit is uncovered.
There is a large difference between a working cognitive simulation model and the more descriptive information processing models as used in reaction time studies (Sternberg, 1969; Sanders, 1983). This is not to say that the latter models are of less importance, but the development of these models is characterized by a somewhat sterile and detached view on possible neurophysiological or even neuro-informatical processes underlying a given reaction time obtained in a specific experimental condition. In our view, one cannot simply label an information processing module with the name "Feature Extraction" without describing how this feature extraction takes place. However, a method like the Additive Factor Method (Sternberg, 1969) has considerable power in systematically guiding the experimentation process along a probable track, and one cannot dismiss the valuable empirical data obtained in this paradigm. Ideally, research in the field would be characterized by a dual-track approach, where a given team consists of a group dedicated to unravel the modular structure of a part of the human information processing system, and a group simultaneously working on the internal architecture of these modules, to create a working model that is satisfying with respect to both the reaction time data and its performance as compared to the empirical data.
Examples of functionality in handwriting production that was previously implicit and that was revealed during the development of our handwriting model are the presence of a module that maintains the base line position of the script trace by feedback and the (currently unresolved) module that solves the horizontal spacing between letters.
Apart from the mentioned advantages, there are also disadvantages to the symbolic information approach that was adhered to until now. To summarize:
- The symbolic processing architecture can be completely different from the biological neural architecture, thereby leading to the definition of processing steps in the model that are absent or unnecessary in the real biological system.
- The stress on symbolic processing interferes with the control of continuous variables.
- The undesirable deterministic, "machine-like", properties cannot be solved by merely injecting stochastic variation in the output of identified processing modules.
ad (1). Marr (1982) describes three levels at which any machine carrying out an information processing task must be understood: (a) the computational theory that describes the goal, the appropriateness and the logic of the used steps, (b) the representation of the information (input/output) and the transformation algorithms, and (c) the hardware implementation. The three levels describe an order that goes from general to specific, from abstract to concrete. It is Marr's belief that the computational description (a) is of importance for any representational mechanism and physical implementation of a system, e.g., a system that can reconstruct three-dimensional estimates of objects that are viewed binocularly. And indeed, the computational description of an information processing capability may be very general and it may potentially lead to the construction of a man-made system that is more powerful than any existing biological system performing this information processing capability. The point is that a computational theory, although certainly necessary for the general insight, can in fact be too general, and that there are no actual representational constructions or physiological machines that in the biological reality are able to perform the computations indicated. Many computational problems are ïll-posed", i.e., there exists no unique solution. Thus, an elegant matrix inversion in computational terms may turn out to be a fallacy in the real world because nature found less elegant, hybrid, solutions for the pitfall of ill-posedness and singularity. As for the second level (b), it is clear that the nature of representations and algorithms that are thinkable at a specific point in time is to a very large extent dependent on the technological and mathematical stage of development. Ultimately, at level (c), the physical characteristics of the systems onder study determine the correctness of the descriptions at the more general levels. Consider, for instance the situation where the goal is to create a simulation model describing the flow of river water in an arborizing estuary. One way of modeling would be the creation of a tree data structure with a decision process controlling the amount of water flowing through the river arms at a node. Clearly, this approach can have success in terms of the accuracy of the estimated water flow quantities. However, such a model does not do justice to the essence of the underlying physical processes. A water flow model in terms of a dynamical system described by differential equations obliterates the necessity of a "homunculus" decision process, the river arms simply being attractors in the system state space.
ad (2). The designation of symbols as basic processing objects gives rise to an interfacing problem: In what way can we step from symbols to a continuous temporal movement pattern? This problem is the complement of the so-called Analog-to-Digital (A/D) problem in categorical perception (Harnad, 1987). Here, unlabeled perceptual input of an analog and continuous nature must be categorized into discrete object representations. In the production of movements conveying the shapes of distinct letters, exactly the opposite problem has to be solved: The Digital-to-Analog (D/A) transform. One solution to the D/A problem is the expansion of symbols at a higher processing level into many more symbols designating infinitesimal steps as an approximation of the continuous flow at the lowest physical level. One could indeed argue that as long as the granularity of the symbol set is fine enough, there is no real problem. The neural process is limited, too, by a baseline noise level that leads to an error that is the parallel of the quantization error of a finite symbolic representation. Another, more parsimonious solution to the D/A problem is the invocation of an interface, as in chapter 7, that transforms a given symbol into a set of quantitative parameters that lead to the production of a fraction of a time function. The latter solution is also used in Morasso et al. (1983) and the minimum jerk models (Edelman & Flash, 1987) to modeling cursive script. The implication of these solutions to the D/A problem is that either there exists an active computational transform, or there exists a "passive" memory association between the symbolic representation of a letter and its corresponding continuous time function. For both the computational transform and the memory association mechanism it holds that a symbolic representation has to be linked uniquely to its (quasi-)continuous counterpart and not to other continuous representations. A severe problem of the symbolic processing approach is the so-called "brittleness" of symbolic information processing systems. Since symbols and rules operating on symbols are monolithic construction entities, there ïs nothing in between them". This makes it hard for such a system to handle novel input information that is not accounted for formally and explicitly. What is needed, in fact, is a new way of thinking about the representation of symbols and quantities in an information processing system (Harnad, 1987; Smolensky, 1988). Especially Reeke & Edelman (1988) vehemently attack the traditional information processing paradigm in artificial intelligence (and cognitive science) as:
"reducing intelligence to symbol manipulation."
ad (3). Since human motor behavior is characterized by both deterministic and stochastic components, a good model should explain the origin of both components. For example, in drawing movements, the amount of movement noise is influenced by context factors (Van Galen, Van Doorn, & Schomaker, 1988). This finding reveals properties that are typical of the neural movement control system. In modeling, it appears to be difficult to simulate the variability of a movement parameter if the modules and processes described by the model do not match the architecture and processes of the real biological system.
A field of modeling cognitive functions that enjoys renewed interest is connectionism, or the simulation of neural networks. The basic feature of all neural network simulations to date is, that they are based on a massive amount of relatively simple processing units (cells) that are highly interconnected. Each unit collects weighed input from a large number of other units and distributes its output to other units. The connections between units are characterized by their weights, which may be positive (excitatory) or negative (inhibitory). The units are characterized by their static transfer function, e.g. a sigmoid function of the net input, and often by a threshold parameter. To some extent such a system has similarities with the biological (often called "wet") neural networks existing in the brain (Smolensky, 1988; Ballard, 1986). For instance, firing rate is often an asymptotic function of the net synaptic input, sometimes sigmoid static transfer functions are found, and there exists a threshold excitation level below which a biological neuron does not fire (Bigland & Lippold, 1954; Kanosue et al., 1979).
But there are also large differences. Apart from some notable exceptions (Torras i Genís, 1986; Peretto & Niez, 1986; Kurogi, 1987), the cells are not stochastic renewal pulse oscillators (Lago & Jones, 1977) in most neural network simulations: They do not fire action potentials in time. The unit activation level is represented by a single value, sometimes even a binary number. Although the firing of an action potential by a biological neuron also is an all-or-nothing process, it is not the single discharge but the current average firing frequency that determines the informational state of a neuron. Also, in biological systems, separate inter-neurons are needed for inhibitory connections which are absent in most simulations. Another serious discrepancy is the fact that biological neurons have a large fan-in/fan-out ratio, i.e., the number of cells that receive information from a given neuron is small compared to the number of cells that send information to this very neuron (Crick, & Asanuma, 1987). The "fully inter-connected nets" that are often used in artificial neural networks are most probably rare in biological reality. Nevertheless, connectionism might be an interesting approach to modeling motor behavior since several neural network simulations have displayed behavior that is comparable to the behavior of biological networks: Learning by examples, generalization, association, robustness with respect to limited damage or internal noise, and graceful degradation in case of limited or noisy input. By graceful degradation is meant the fact that a network exhibits "reasonable" behavior if it is presented with noisy input. By contrast, deterministic syntactic systems, such as rule based expert systems, often get stuck in an inappropriate system state if presented with noisy data or data for which no explicit rules are defined (Reeke & Edelman, 1988).
Before trying to answer the question if this approach can solve the problems in cognitive and motor modeling raised above, let us give a short review of some of the basic architectures and models used, referring to their usefulness in the simulation and recognition of handwriting whenever applicable. For each of the models, some attention will be given to Architecture, Operation, Learning, and to Practical Issues.
1 Two-layer network architectures: Linear Classifier and Perceptron
One of the earliest ärtificial neural networks" is the linear classifier.
Figure 1 gives a schematic description of the architecture of a linear classifier (and the perceptron). There are three system components: (1) A layer of input units (cells, neurons), (2) a bundle of connections to (3) a layer of output units. In the sequel we will include the input cell layer in the counting of the number of layers. In this terminology, a linear classifier is a two-layer network. An N-layer network will have N-1 connecting bundles, where a bundle can be described as a two-dimensional weight matrix W. The rationale for this nomenclature is the realization that the input units may have their own properties (e.g., static and dynamic transfer function) and thus contribute to the network characteristics. The connections in the bundle also have their specific properties (connection sign and strength, delay).
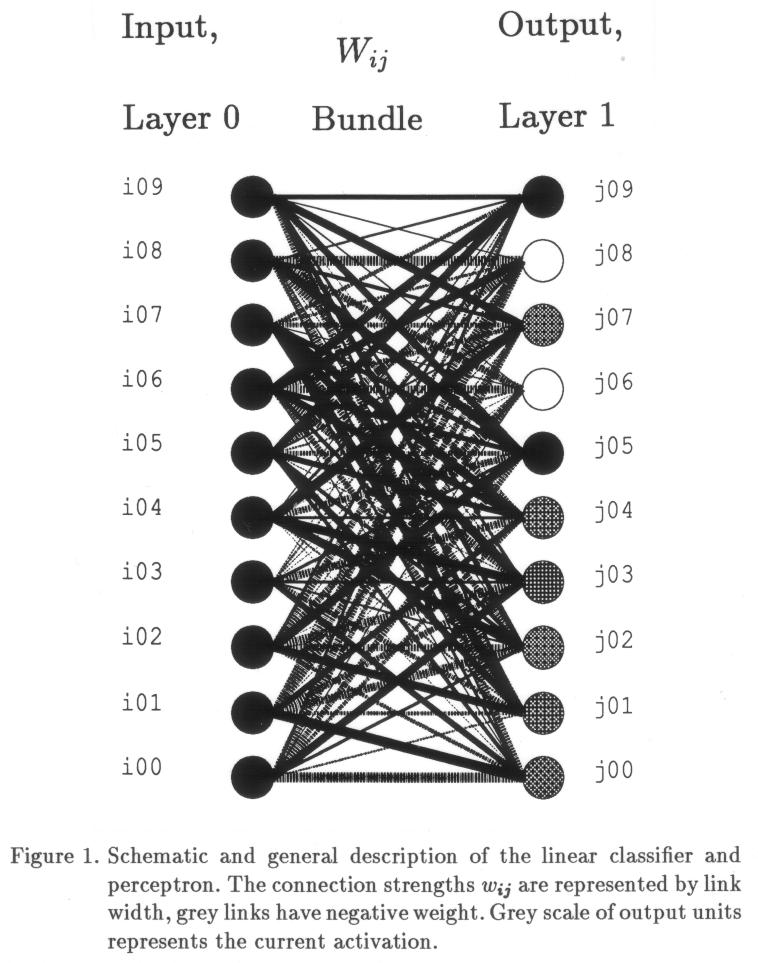
Assume an n-dimensional space Fn, where each dimension denotes a perceptual feature of observed objects O. The vector [i\vec]k containing n feature values, describes object k in Fn. Now assume a set of object classes K = {j1,jm}. The goal is to classify a given feature vector [i\vec]p as describing an object peK. In linear classification, this is done by specifying an objective function opj for each object class j, given pattern p, such that:
| (1) |
that is, the activation of an output cell j is the linear combination of the feature vector elements. A winner-take-all decision leads to the choice of the object class, read ünit", j for which opj is maximal. This relation is possible if the vectors describing the object classes are linearly separable.
In fact, for the linear classifier, the output unit activation function is a linear function of the net synaptic input x:
| |||||||||||||||
| (2) |
| (3) |
For the perceptron, both input and output units can only assume the value of 0 or 1. The output unit activation function is:
| (4) |
| (5) |
An often-used learning rule in artificial two-layer network is the Hebbian rule:
| (6) |
In words: A connection between input unit i and output unit j is strengthened if both units are active in input pattern [i\vec]p and target output pattern [t\vec]p. Using a Hebbian learning rule, inputvectors [i\vec] must be orthogonal ([i\vec]Tp[i\vec]q = 1 if p = q and 0 otherwise). This rule does not depend on the current state of the weight matrix.
Another well-known rule is the delta rule, also called Least Mean Squares (LMS) or Widrow-Hoff rule:
| (7) |
| Input | Output | |
| i1 | i2 | o1 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The problem with linear classifiers and perceptrons is that they cannot solve a problem like the exclusive-or (XOR) mapping. Table 1 gives the state table for this mapping. It is clear that there are no possible weights in a (2x1) architecture such that the linear combination w11i1+w12i2 = o1 for all states of i and o. For many problems, the functionality of a two-layer network is sufficient. An experiment with a two-layer network will be reported in Chapter 6, where its ability to learn a typical non-linear function is illustrated.
2 Multi-layer networks and learning by error back propagation
Two-layer networks are only able to solve a limited set of classification, association or transformation problems. If more, so-called hidden, layers are introduced, difficult transformations on non-orthogonal and not linearly separable data can be performed. This is only true if the static unit transfer function of the units in the hidden layers is a continuous, differentiable non-linear function.
Typically, multi-layer networks are characterized by the number of units per layer in the following notation: (nin x nhidden1 x...x nhiddenm x nout), e.g., (4x8x2) for a three-layer network.
The operation of a multi-layer network is as follows. Each cell j collects the afferent activity of cells i in the preceding layer:
|
|
The standard delta rule in case of a two-layer network without hidden units pertains to the modification of a weight w between an output unit j and an input unit i:
| ||||||||||||||
The generalized delta rule has the same form as the standard rule (Rumelhart, Hinton & Williams, 1986):
| (9) |
| (10) |
p. 327
where: f¢j(xpj) is the derivative of the unit activation function that transforms the sum of the activations xpj received at j from cells in the previous layer (xpj = åi wjiopi+qj). The unit activation function is (Rumelhart, Hinton & Williams, 1986):
| ||||||||||||||||||
p. 329
Its derivative simply being opj(1-opj), so the generalized delta rule rewrites as:
| (12) |
In words, roughly, the generalized delta rule reads as follows. Weight change during learning is proportional to the product of learning rate, the activity of the sending unit and the error of the activity of the receiving unit, or a weighed error of the activity of all the receiving units in case the latter belong to a hidden layer. The error itself is weighed by a function (the first derivative of the unit activation function) that leads to a maximum weight change if the activation of the receiving unit equals its threshold (bias) level q.
Whereas thresholds in biological networks are an inherent property of the neuron, in artificial or theoretical networks, a threshold can be defined as a connection strength to an auxiliary unit not part of the input, hidden, or output layers, that is continually exhibiting a constant activation level. This redefinition allows for the incorporation of threshold level adaptation during a learning process. In case of back propagation this implies that the generalized delta rule applies to both connection weights and threshold levels.
As Hecht-Nielsen (1987) notes, most applications of back propagation deal with mappings from binary input patterns to binary output patterns, although there is no fundamental objection against using vectors of non-binary activation patterns. This issue will be studied in an experiment to be described later (Chapter 6). There is no inherent provision for the representation of time, an essential aspect in the modeling of handwriting which will be addressed in Chapter 7. In Chapter 8, the capabilities of the multi-layer perceptron in finding a solution to an important mapping problem in motor control (and handwriting) are assessed: The autonomous learning of an internal representation of the effector system.
3 Hopfield networks
Hopfield (1982) networks are characterized by a single layer of fully interconnected units. The activation level may assume two values, true or false, mostly represented by +1 and -1, respectively. In statistical physics, such a system is a model for a material which consists of atoms with an amorphous distribution of Ising spins, spin glass, (Stein, 1989). The units are connected by links with a specific real-valued positive or negative weight.
The basic functions of a Hopfield network is pattern completion (association). In pattern completion, the activation of a number of units is set (clamped) according to an incomplete binary pattern, a perceptual input, so to speak. The activation of a unit can be interpreted as a hypothesis concerning the existence of some perceptual feature. Subsequently, the system is left to evolve states according to the constraints that are formed by the clamped units and the weights of the connections. The weights of the connections are based on a learning process in which the system was confronted with several complete binary patterns. If there is a solution, the system will converge to a final state in which the activation of the units represents the complete pattern. This is possible because in the relaxation phase, the activation of single units changes such that the total system energy decreases. The total system energy in a Hopfield network is:
| (13) |
(Hopfield & Tank, 1985, p. 144.) 8
| (14) |
(Hinton & Sejnowski, 1986, p. 286)
where E is the system energy, wij is the synaptic weight from the jth to the ith unit, si is the state of the ith unit and may be -1 or +1 (sometimes 0 or 1), qi is the threshold of unit i. Updating states si is achieved by switching each unit i into whichever of its two states yields the lower total system energy given the current state of the other units j ¹ i. The activation of a unit k can be seen as a hypothesis. The contribution to the change in energy by a change of this hypothesis can be locally determined at k and its connected units by
| (15) |
(Hinton & Sejnowski, 1986, p. 286; Hopfield, 1982, p. 2556)
Minimizing the energy contributed by a unit is achieved by adopting true (+1) if the sum of its inputs exceeds its threshold, i.e.,
| (16) |
| (17) |
In pattern completion, a number of units is clamped to a known part of a binary pattern, and the problem to be solved is the completion of the total pattern. In this case the inter-units connection strengths wij are based on a learning procedure. If a Hopfield-type network is used for constraint solving, the constraints are translated into a set of wij values and the question is what binary pattern represents a (near)-optimal energy state of the net. The problem with the deterministic updating procedure described above is that it can lead to infinite oscillations. Kirkpatrick et al. (1983) developed a solution that is borrowed from statistical mechanics. This solution is used by Hinton & Sejnowski (1986) in a constraint solving algorithm dubbed "Boltzmann machine", to be discussed later.
In Hopfield networks, an often used learning rule is the Hebbian rule (eq. 6). In case of Hopfield nets weight change after the presentation of pattern p is:
| (18) |
The weight matrix can be determined non-iteratively by:
| (19) |
| (20) |
Practical issues in Hopfield networks involve the distinction between synchronous and asynchronous update of unit activities, the presence of transmission delays in the links and the learning rule that is used to determine the initial weights in association problems. Other issues are the updating of thresholds qi, and the pre-structuring and limiting of the connectivity (Gielen & Coolen, 1989). A problem with Hopfield networks is that the choice of patterns is not free. In the original paper only a number of 15 patterns could be recalled without error, using 100 units (Hopfield, 1982). The Hamming distance (the sum of differing bits) between the patterns must be ßufficient", Hopfield mentions a distance of 50 for N=100 units. Probabilistically, the number of patterns is of the order N/log(N) (McEliece et al., 1987). Structuring or shaping of the weight matrix on the basis of the available patterns can improve the storage capacity (Coolen & Ruijgrok, 1988). The potential use of the Hopfield network in motor modeling has been shown in an inverse dynamics experiment (Gielen & Coolen, 1989). Further research with respect to the modeling of handwriting processes with this type of network is planned.
4 Boltzmann machines
The principle of describing a system state with zeros and ones, zero-one programming, can be used in constraint solving (Kirkpatrick et al., 1983). Practical examples are the traveling salesman problem, finding a good lay-out of components on a silicon chip, loading a ship with varying-size packets, etc.. Here, the binary state vector represents hypotheses that are being generated stochastically (Metropolis et al., 1953). Hypotheses can be mutually consistent or conflicting in a gradual fashion. This can be represented by assuming a positive or negative weight value between hypotheses, yielding a weight matrix similar to the case of the Hopfield network. This weight matrix is generally not learned, but determined by the constraints that are given. The constraints are called "weak", because single constraints may be violated, in favour of a better overall solution.
After determining the (symmetrical) weight matrix wij, the system is left to evolve states according to the constraints that are formed by the clamped units and the weights of the connections. The state of unit (hypothesis) k, sk is stochastically set to true with a probability:
| (21) |
(Hinton & Sejnowski, 1986, p. 288)
where T stands for a temperature parameter that determines the amount of ("thermal") noise in the unit firing process. In thermal equilibrium, the relative probability of a global system state a with respect to state b is:
| (22) |
(Hinton & Sejnowski, 1986, p. 289)
where Ea and Eb represent the energy in global states a and b, respectively. Thus, given T, this ratio depends only on the energy difference between the two system states. This equation describes the well-known Boltzmann distribution. In a typical simulated annealing scheme the system starts off with a high temperature, yielding large state changes and allowing for large jumps in E. Gradually, T is decreased, such that the process will escape from local minima in E and, hopefully, will reach the absolute minimum. The state of the units then finally represents the solution to the imposed constraints.
A Boltzmann machine can operate as an input/output mapping or pattern completion device. In this case, the constraints are formed by (a) a set of units that are clamped to the values of a pattern, and (b) the weight matrix. The weight matrix wij should be learned. By calculating the probabilities pij+ (some units clamped) for a unit being ON, and pij- (all units unclamped) for a unit being OFF, at the end of the annealing phase, weight changes can be imposed: DWij = h(pij+ - pij- (Hinton & Sejnowski, 1986). This method is cumbersome and slow, and depends heavily upon the annealing schedule.
The slowness of the method, especially if implemented in a sequential computer, makes it necessary to find an annealing schedule (the function of temperature T over cycles in the relaxation phase) that is as short as possible. However, theoretically, no finite-length relaxation phase guarantees that the obtained optimum is global (Richards, 1990). Other solutions are the implementation of the Boltzmann machine in VLSI silicon chips containing the necessary multiply-add functions and random number generators (Pesulima, Pandya & Shankar, 1990). In the current project, the Boltzmann machine is used in cursive handwriting recognition, as reported in a master's thesis under supervision by the author (Stal & Ter Hofstede, 1990). In cursive handwriting recognition, as will be explained in chapter 9, a solution search space is created in which an optimum solution for the word to-be-recognized has to be found. Traditionally, this is done using deterministic tree search techniques (Tanaka et al., 1982). In the case of varying-length discrete sequences, tree search is computationally expensive, hard to parallelize, and does not elegantly handle noisy fragments in an otherwise neatly written input word. The Boltzmann machine can be used to integrate information from a number of sources (pattern shape quality, digram probabilities, amount of input covered by a character hypothesis etc.) in a parallel fashion. These information sources impose constraints that determine the ënergy landscape" of the solution space for a word. Initial results are promising, but more study is needed with respect to the choice of constraints, and with respect to the method of translating of these constraints into a weight matrix Wij.
5 Self-organizing networks
As an example of self-organizing networks we will only handle Kohonen nets for unsupervised feature vector quantization, the Topology Preserving Maps, although there exist other models, like Adaptive Resonance Theory (Grossberg, 1987).
Kohonen (1987) has looked at the neural architecture in the cerebral cortex to develop a self-organizing feature vector quantization network. The cerebral cortex can be considered as consisting of a large number of cellular columns with high inter-connection in the vertical direction and a limited connectivity in the horizontal direction. In this section we will use the term "column" instead of ünit". All columns receive a common input consisting of a fixed number of channels, each column j having its own connection strength wij to the input channels i. Furthermore, each column receives input from other columns with strength vkj. Auto-recurrent inputs j = k, i.e., vkk can also be present.
After presentation of an input pattern, the cell column that exhibits the largest activation value represents the output state corresponding to that input pattern. In this sense, the Kohonen network is a local, topological model instead of a distributed model. The activation level represents a certainty measure. It is one of the virtues of the Kohonen model that the development of activation in time is an essential characteristic, just as in the biological reality. Therefore, some of the following equations will be differential with respect to time t. Changes in the activation value of a column are given by:
| |||||||||||||||||||||||
| (24) |
Kohonen (1987) has developed a number of useful learning rules. A general formula for weight change in Kohonen nets is:
| (25) |
One difference between the Kohonen network and the other types mentioned so far is the fact that it is not a distributed model. Furthermore, there is a difference in the use of the concept of "weight". In the feature vector quantization network, the weight values are in the same domain as the sensory inputs, whereas their scaling in multi-layer networks is only indirectly related to input magnitudes. The Kohonen network is currently used in a ßpeech-to-phoneme code" translator (Kohonen, 1988). However, to recognize speech it is not sufficient to classify isolated phonemes. The resulting varying-length sequence of phonemes must be converted to a varying-length sequence sequence of letters. Other architectures are more plausible here (cf. Chapter 9). Kohonen networks are successfully used in the classification of strokes in cursive script (Morasso et al., 1990). Figure 2 shows a topological map of stroke shapes such as used by the cursive handwriting recognizer that is under development in Esprit project P419 in cooperation between the NICI, Nijmegen and the University of Genova.
6 Three experiments on connectionism in motor control.
As we have seen thus far, most of the applications of neural network simulations involve perception or memory models. With respect to modeling motor behavior, we shall now focus on some fundamental issues in motor behavior neural network models must be able to address: (1) Movement patterns must be described by continuously varying control variables, (2) movement occurs in time and different movement patterns are chained into sequences, (3) controlling and coordinating movement requires complex transformations of sensory to motor representations.
In the next three chapters, we will describe three simulation experiments to explore the typical characteristics of common artificial network models if applied to modeling motor control and handwriting movements in particular:
- Chapter 6: Representation of quantity
- Chapter 7: Representation of time and sequence
- Chapter 8: Representation of the effector system
Where possible, these experiments are performed on the basis of kinematic motor aspects in handwriting.
7 References
Ballard, D.H. (1986). Cortical connections and parallel processing: Structure and function. Behavioral and Brain Sciences, 9, 67-120.
Bigland, B., & Lippold, O.C.J. (1954). Motor unit activity in the voluntary contraction of human muscle. Journal of Physiology, 125, 322-335.
Coolen, A.C.C., & Ruijgrok, Th.W. (1988). Image evolution in Hopfield networks. Physics Review, A38, 4253ff.
Crick, F., & Asanuma, C. (1987). Certain aspects of the anatomy and physiology of the cerebral cortex. Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Volume 2 Psychological and Biological Models (pp. 334-389). Cambridge, MA: MIT Press.
Edelman, S., & Flash, T. (1987). A model of handwriting Biological Cybernetics, 57, 25-36.
Grossberg, S. (1987). Neural Networks and Natural Intelligence., Cambridge: MIT Press.
Gielen, C.C.A.M., & Coolen, A.C.C. (1989). Self-organization in neural networks underlying the coordination of movements. In J. Schopman (Ed.), Publications Series. Vol 24. Utrecht: The department of epistomology and philosophy, Utrecht University (The Netherlands)
Harnad, S. (1987). Category Induction and Representation. In S. Harnad (Ed.), Categorical Perception (pp. 535-565). Cambridge: Cambridge University.
Hinton, G.E. and Sejnowski, T.J. (1986). Learning and Relearning in Boltzmann Machines. In: J.L.McClelland, D.E. Rumelhart and the PDP research group (Eds.), Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Volume 1 Foundations (pp. 282-317). Cambridge, MA: MIT Press.
Hopfield, J.J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences, USA, 79, 2554-2558.
Hopfield, J.J. & Tank, D.W. (1985). "Neural" computation of decisions in optimalization problems. Biological Cybernetics, 52, 141-152.
Kanosue, K., Yoshida, M., Akazawa, K., & Fujii, K. (1979). The number of active motor units and their firing rates in voluntary contraction of human brachialis muscle. Japanese Journal of Physiology, 29, 427-443.
Kirkpatrick, S., Gelatt, C.D., & Vecchi, M.P. (1983) Optimization by simulated annealing. Science, 220, 671-680.
Kohonen, T. (1987). Adaptive, associative, and self-organizing functions in neural computing. Applied Optics, 26, 4910-4917.
Kohonen, T. (1988). The "neural" phonetic typewriter. IEEE Computer, March, 11-22.
Lago, P., & Jones, N.B. (1977). Effect of motor unit firing time statistics on EMG spectra. Medical & Biological Engineering & Computing, 15, 648-655.
Marr, D. (1982). Vision: A computational investigation into the human representation and processing of visual information. San Francisco: Freeman, p. 25.
McEliece, R.J., Posner, E.C., Rodemich, E.R., Venkatesh, S.S. (1987). The capacity of the Hopfield associative memory. IEEE Transactions on Information Theory, 33, 461-482.
Metropolis, N., Rosenbluth, A.W., Rosenbluth, M.N., Teller, A.H., & Teller, E. (1953). Equation of state calculations for fast computing machines. Journal of chemical physics, 21, 1087-1092.
Morasso, P., Mussa Ivaldi, F.A., & Ruggiero, C. (1983). How a discontinuous mechanism can produce continous patterns in trajectory formation, Acta Psychologica, 54, 83-98.
Morasso, P., Kennedy, J., Antonj, E., Di Marco, S., & Dordoni, M. (1990). Self-organisation of an allograph lexicon. International Joint Conference on Neural Networks, Lisbon, March 1990.
Peretto, P., & Niez, J.-J. (1986). Stochastic dynamics of neural networks IEEE transactions on systems, man, and cybernetics, 16, 73-83.
Pesulima, E.E., Pandya, A.S. & Shankar, R. (1990). Digital implementation issues of stochastic neural networks. Proceedings of the IEEE International Joint Conference on Neural Networks 1990 Vol. II, 187-190.
Reeke, G.N., & Edelman, G.M. (1988). Real brains and artificial intelligence. Daedalus, 117, 143-173.
Richards, R. (1990). An efficient algorithm for annealing schedules in Boltzmann machines. Proceedings of the IEEE International Joint Conference on Neural Networks 1990 Vol. I, 309-312.
Rumelhart, D.E., Hinton, G.E. & Williams, R.J. (1986). Learning internal representations by error propagation. In J.L.McClelland, D.E. Rumelhart and the PDP research group (Eds.), Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Volume 1 Foundations (pp. 318-362). Cambridge, MA: MIT Press.
Sanders, A.F. (1983). Towards a model of stress and human performance. Acta Psychologica, 53, 61-97.
Smolensky, P. (1988). On the proper treatment of connectionism. Behavioral and Brain Sciences, 11, 1-74.
Stal, K. & Ter Hofstede, O. (1990). Word completion by multiple constraint solving. Masters Thesis. Nijmegen University (The Netherlands): Computer Science, dept. of real-time systems.
Stein, D.L. (1989). Spin glasses. Scientific American, 261, 36-42.
Sternberg, S. (1969). The discovery of processing stages: Extensions of Donders' method. Acta Psychologica, 30, 276-315.
Tanaka, H., Hirakawa, Y., & Kaneku, S. (1982). Recognition of distorted patterns using the Viterbi algorithm. IEEE transactions on patterns analysis and machine intelligence, 4, 18-25.
Torras i Genís, C. (1986). Neural network model with rhythm-assimilation capacity. IEEE transactions on systems, man, and cybernetics, 16, 680-693.
Van Galen, G.P., Van Doorn, R.R.A., & Schomaker, L.R.B. (1988). Effects of motor programming on the power spectral density function of writing movements. Journal of Experimental Psychology, 16, 755-765.
Chapter 6
Representing quantity and learning a non-linear function
1 Introduction
In the development of a neural network model of handwriting it is essential to study the ways a quantity, e.g., a vertical displacement DY, can be coded in a neural architecture. Since most of the work on neural networks is concentrated around learning rules, the coding of quantity is often a neglected issue. Basically, three viewpoints can be found:
- The representation of quantity by the firing rate of a neuron (rate coding).
- Representing quantity by the topology of a set of supra-liminally firing neurons (value unit coding).
- Representing quantity by the sum of the activations of a set of neurons
(recruitment coding).
The representation of a quantity by firing rate is an issue of hot debate (Ballard, 1986). Proponents of this view (Pellionisz, 1986) state that firing rate control has been proven to exist in the biological neural system and has important advantages in terms of the number of neurons needed to represent a certain quantity. Opponents have indicated the limited amount of information (bits) that can be sent through a single axon due to the inherent noise of the system and the fact that it requires at least an inter-pulse interval for a neuron to get an update of the äverage" firing rate. In most artificial neural network models, the firing rate is represented by a single real value. In this view, the firing rate conveys only the certainty or probability of the value or quantity portion that is encoded by a single unit. In a coding scheme proposed by Ballard (1986), a quantity is represented by the activity of a single unit (i.e., a single neuron, or a cluster of neurons). The firing rate transfer function of this unit has an inverted U-shape, peaking at the afferent quantity that it represents. The advantage of this coding principle is that functions requiring multi-dimensional scaling of several different inputs can easily be implemented by units that receive activity of several value units representing values at different dimensions. For instance, the combined output for a feature extractor that detects lines at an angle of 45 degrees and a feature extractor that detects a specific hue of green leads to the configuration of a new feature extractor detecting slanted green lines. Opponents have pointed out the large number of units needed in this type of coding. This is known as the Nk problem where N represents the number of units representing a dynamic range (granularity), and k determines the number of (e.g., sensory) dimensions to be coded.
A type of coding that is well-known to researchers in the field of motor control is recruitment. In recruitment, quantity is coded by the number of neurons in a fixed pool that are supra-liminally active at a given moment in time. Recruitment coding has been used in a two-layer network model for the coding of joint angle values in an inverse dynamics problem (Gielen & Coolen, 1989). As in value unit coding, the number of neurons determines the accuracy of the coding scheme. If all units have a maximum output level of equal value, and if the firing thresholds are distributed uniformly over the dynamic range to be covered by the coding scheme, the relationship between net input and net output approaches linearity. Conversely, non-linear mapping can be achieved by a non-uniform distribution of thresholds and by differences in maximum output level over neurons in the pool.
Another encoding scheme, artificial, but optimal from the point of view of information theory, is the binary encoding of quantity by units, leading to the maximal resolution of 2n quantity levels for n binary units. Binary coding is a typical topological coding scheme. Multi-dimensional coding schemes are conjunctive and coarse coding (Hinton, McClelland & Rumelhart, 1986). Coarse coding is an extension of value unit encoding in which a number of neighboring units are part of a zone that represents a given quantity.
Irrespective of the type of coding, it is doubtful whether the activity of
a single neuron in the cerebral
cortex is sufficient to represent a quantity
reliably. If a quantity is represented by the modal firing frequency of a
cluster of neurons, rate coding will be robust with respect to the
dependence on single-neuron activity. Furthermore, the argument of the reduced
information capacity of single axons does not hold strictly any longer for the
case of a nerve bundle emanating from such a
cluster of neurons, if the firing
of the neurons takes place
asynchronously.
Likewise, in value unit coding,
the representation of a quantity by the location of a cluster of firing neurons
will increase the fault tolerance as compared to the case of a single neuron.
Here also, asynchronous
firing within the cluster will result in a
temporally more stable
representation
as compared to the case of a single neuron.
The recruitment coding scheme is interesting as a general model for the coding of quantity because of its known presence in spinal alpha-motoneurons and the mathematical models that have been developed (De Luca, 1979; Blinowska, Verroust & Cannet, 1979; Lago & Jones, 1977; Agarwal & Gottlieb, 1975; van Boxtel & Schomaker, 1983). In a ventral horn of a spinal segment, the alpha motoneurons are grouped into pools, each pool for a different muscle. The axon of a single alpha motoneuron terminates on a number of muscle fiber end plates. The combination of an alpha motoneuron and its connected muscle fibers is called a motor unit. The total activation of a muscle is determined by the sum of the activations of the alpha motoneurons in a pool. As the activation of the pool by supra-segmental or segmental input increases, (1) single motoneuron firing frequencies are increasing, and, (2) more motoneurons are being recruited, i.e., exhibiting a supra-liminal firing rate. The recruitment occurs in a fixed order, starting with small motoneurons innervating a limited number of muscle fibers, and gradually including larger and larger motoneurons that innervate large numbers of muscle fibers. Thus, in this scheme, quantity is encoded by a combination of firing rate and recruitment of a number of neurons. The physiologically existing scheme of recruitment coding solves the problem of limited information content of the output of a single neuron, it allows for the easy coding of non-linear relationships, it exhibits reduced sensitivity to the effects of inter-pulse durations because of the gap-filling accumulation of multi-unit activity, and it is robust with respect to noise and single-unit failure. Apart from the alpha motoneurons, it has been shown that on the afferent side, mixed recruitment and firing rate control is the mechanism by which lumped muscle spindle activity reliably reflects muscle stretch (Milgram & Inbar, 1974).
Since the goal of this study is the development of an artificial neural network model of handwriting, it is important to find out if there are differences between the quantity coding schemes mentioned above, if they are implemented in an artificial neural network. A question, for instance, concerns the learning speed in a recruitment coding scheme as compared to a value unit coding scheme.
In order to study the behavior of several coding schemes in an artificial neural network, a series of simple experiments was performed with the standard three-layer network taught by back propagation (Rumelhart, Hinton & Williams, 1986). This model is not a pulse oscillator model: unit activations are represented by a single real value reflecting the average firing frequency of the biological unit. The network had to learn the static mapping from f to sin(f) with f = [0,2p], i.e., a single period of the sinusoid. Note that the mapping is non-dynamical, the network does not learn to oscillate. A period of the sinus was chosen because it exhibits typical aspects of non-linearity: the existence of extrema and a bending point. The "difficulty" of the mapping lies in the fact that a single given output activation pattern can be produced by several input activation patterns (i.e., values for f). There were four coding conditions.
- Single-unit Activation level (SA),
- Multi-unit Recruitment and Activation level(MRA),
- Multi-unit Topology and Activation level (MTA),
- Multi-unit Topology, Binary coding (MTB).
Table gives the theoretical coding accuracy of the multi-unit coding schemes if unit activation were a binary threshold function, and fine tuning by activation level (denoted by Ä" above) were not the case. It is expressed as a proportion of the total dynamic range to be coded, given N units.
| Coding Scheme | Accuracy | |
| Recruitment | (MR) | 1/N |
| Value-units | (MT) | 1/N |
| Binary | (MTB) | 1/2N |
According to these limits, if accuracy were the most important characteristic, the more or less technical binary coding scheme (MTB) would be optimal. Clearly, in biological systems, pure binary coding did not emerge in the course of evolution. With respect to accuracy, there is no difference between a topological or value-unit scheme (MT) and a recruitment scheme (MR) without fine tuning by the unit activation levels. There is, however, another characteristic that is of importance in a physical system: fault tolerance or robustness of the coding scheme. Table gives an overview of the theoretical error sensitivity in the decoding of activation patterns of the multi-unit coding schemes. The expected error values are based on the assumption that the activity of units is unreliable, i.e. has a non-zero probability of exhibiting the inverted activation value, one single unit at a time. From this table, we see that recruitment coding (MR) is much more tolerant to erroneous unit activity than value unit coding (MT). Value unit coding (MT) appears to be the most vulnerable coding type, yielding an average error of 1/2. In binary coding, there is the situation that the maximum error (1/2) is large as compared to the average error (Avg. e® 1/N) for large numbers of units. This indicates that a binary coding scheme is particularly sensitive to the shape of the error probability distribution over units. This latter point may be an explanation for the fact that pure binary coding did not evolve in natural systems. The aim was to see how accurate and fast a network could be taught a sin() function for the different encoding schemes.
| Coding Scheme | Min. e | Avg. e | Max. e | |
| Recruitment | (MR) | 1/N | 1/N | 1/N |
| Value-units | (MT) | 1/N | 1/2 | 1-1/N |
| Binary | (MTB) | 2-N | (2N-1)/(N2N) | 1/2 |
2 Method
For all schemes, the static transfer function of a hidden or output unit is the sigmoid (eq 11). The dynamic range of the unit activation is taken as oj = [omin,omax] to ensure that weight values ® ¥ did not occur. The domain of f = [0,2p] and range of sin() = [-1.,+1.] were each linearly mapped to [omin,omax]. The actual values for omin and omax were 0.1 and 0.9, respectively. The learning rate h was set to 0.4, and a first-order recursive filter with a gain of 1 (a = 0.4,b = 0.6) was used to flatten changes in Dwij during gradient descent. This approach has the advantage over the normal "momentum term" that the effects for the learning factor h and the smoothing filter can be separated. On the contrary, the standard momentum term (Rumelhart, Hinton, & Williams, 1986) leads to a reduced effective learning rate. The target function is given in table .
There were 1250000 presentations of an input/output pair (f,sin(f)) picked at random from the list, using a uniform distribution. Since there were 19 input/output pairs, there is an average of 65790 presentations of the pattern as a whole (ëpochs"), in each training session. Given these general parameters, the independent variables were: coding scheme, number of input units, number of hidden units, number of output units. The dependent variables are accuracy of the mapping, or Signal to Noise ratio DS/N, expressed in dB, i.e.,
| |||||||||||||||||
The Single-unit Activation SA coding scheme is characterized by a 1xNx1 architecture. The activation level of the input unit varies linearly with f, the activation of the output unit varies linearly with the required sin().
In the Multi-unit Recruitment and Activation MRA scheme, a number of input units is used, as an analogy to an alpha motoneuron pool exhibiting a fixed recruitment order. The main difference with the biological version is the fact that the maximum unit activation is equal for all units. The input layer is organized as a linear array of units, a low index indicating low activity, a high index indicating high activity. As the total input excitation increases, more units become active. Sometimes, this scheme is called "thermometer coding". Encoding a value for an input layer is as follows. If x is a real-valued quantity with a dynamic range of [xmin,xmax], and n is the number of units in an input or output layer, then the real number of active units u is
| (3) |
| (4) |
| (5) |

In a pure value-unit coding scheme (Multi-unit Topology, MT), only the position of a single active unit is of importance. To visualize this coding type, one can think of a single LED in a linear array being active to represent a value ("flying spot coding"). In the current experiment, a new scheme MTA is proposed in which the activity level of two adjacent units in a layer is used to encode ïntermediate" values for fine tuning of the quantity. The position of the first active unit is l = int(u) using u from 3. The activations of units l and l+1 are:
| ||||||||||||||
| (7) |

For reasons of comparison, a simple binary coding (Multi-unit Topological Binary MTB) scheme was used. The binary coding is interesting because it is the optimum accuracy scheme for a set of binary threshold units. In binary decoding, the topology of an activation pattern is obviously crucial. The threshold used in decoding was simply (omax-omin)/2 = 0.5. Figure 3 gives an example of patterns obtained in this artificial coding scheme MTB.

3 Results
As a check, the accuracy of the coding schemes SA, MRA, and MTA were calculated and appeared to be 144 dB, which is consistent with the accuracy of seven decimal places for the VAX single-precision floating point representation. The accuracy of the MTB scheme appeared to be consistent with the rule "6 dB/bit", i.e. 30.5 dB for a five-unit encoding, 60.6 dB for a ten-unit encoding. These figures represent the maximum obtainable accuracy in single-precision floating point calculation. Steepest learning rates are observed below 16000 epochs. After this number of presentations, the DS/N value either approaches asymptotic levels or is slowly increasing.
In its simplest form, the Nx1 architecture, the mapping problem is reduced to a simple pseudo-linear model, or table search (e.g., a trivial 19x1 network). Table shows the values of DS/N at the tail of the learning curve (1250000 I/O pairs, 65789 epochs), for a number of input units of N = 5 and N = 10. As is clear from the table, the accuracy of the input/output mapping deteriorates as M is increasing. This effect is much stronger in the case of Value Unit coding than it is in the case of Recruitment coding. Input and output layers are subject to the same coding scheme. Concerning other experiments the following observations were made. The binary coding scheme in the NxM architecture never displayed an accuracy above 12 dB. The 1xN architecture never reached a sinusoid shape. The Nx1 architecture requires at least N = 3 to approach the sinusoid shape. In a network with N = 1 and N = 2, only a monotonically increasing output was obtained with a sigmoidal shape.
| Output units | Value Unit (MTA) | Recruitment (MRA) | ||
| (M) | N = 5 | N = 10 | N = 5 | N = 10 |
| 1 | 22.86 | 40.81 | 22.88 | 53.56 |
| 2 | 17.96 | 27.40 | 23.47 | 27.39 |
| 3 | 14.07 | 16.49 | 17.74 | 27.06 |
| 4 | 7.81 | 22.54 | 18.90 | 33.22 |
| 5 | 4.19 | 17.51 | 19.23 | 32.93 |
| 6 | 2.40 | 12.96 | 16.08 | 29.32 |
| 7 | 2.56 | 13.24 | 17.72 | 32.02 |
| 8 | 1.93 | 10.75 | 17.62 | 31.95 |
| 9 | 2.86 | 10.91 | 16.83 | 30.26 |
| 10 | 1.30 | 7.72 | 16.91 | 33.79 |
This architecture, which is a model for a single-unit receptor/single-unit effector connected via an intermediate layer of variable size, reveals the network capability of "finding its own" intermediate representation of quantity in the hidden units. The coding scheme is Single-unit Activation
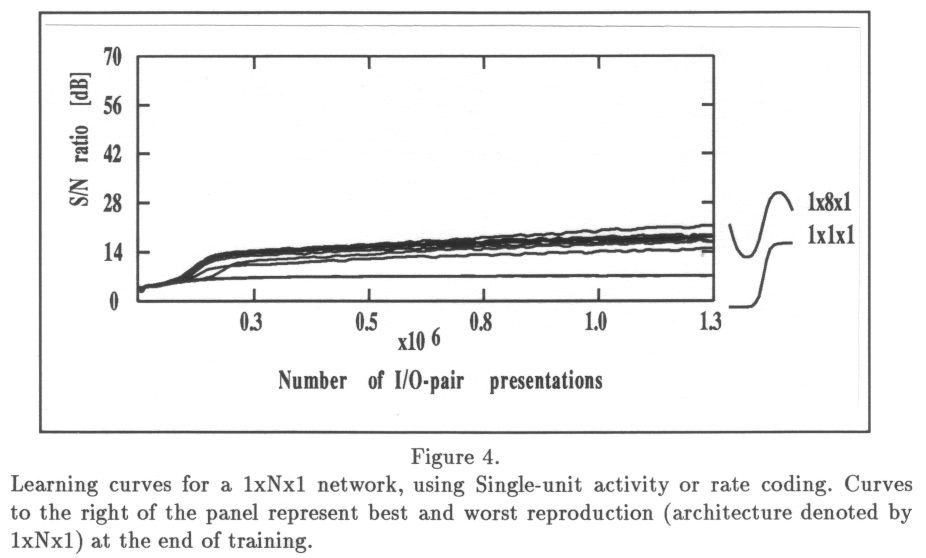
or rate coding. Figure 4 shows the learning curves for 1xNx1 architectures with N varied from 1 to 10. Please note that the learning curve represents the effective error in the target domain (the sin() function) rather than the average error of the individual unit activation which is the basis for the error back propagation during learning. A 1x2x1 architecture never reaches the sinusoid shape and produces a sigmoid output function. In general, the accuracy increases as the number of hidden units N increases, but this relationship is not completely monotonous within the used range of number of hidden units (Table ). The obtained level of accuracy is low.
| Hidden units | Single-unit |
| (N) | activation (SA) |
| 1 | 7.18 |
| 2 | 7.20 |
| 3 | 14.89 |
| 4 | 16.91 |
| 5 | 17.11 |
| 6 | 18.27 |
| 7 | 18.24 |
| 8 | 21.48 |
| 9 | 18.64 |
| 10 | 18.73 |
Here the effect of the input coding scheme is tested, using N = 5 or N = 10, varying the number of hidden units, and assuming a single output unit (SA or rate coding). Table shows the Signal to Noise ratio for the three coding schemes. In case N = 5, value unit coding (MTA) yields a higher accuracy than recruitment coding (MRA), but this difference disappears for N = 10. In general, the accuracy slightly improves with an increasing number of units in the hidden layer, except in the case of binary coding (MTB), where this relation is irregular. Maximum accuracy is obtained in the binary coding scheme, but the accuracy is highly dependent on the number of hidden units. A number of input units N = 10 yields a much better performance than the case of N = 5, for all coding schemes.
| Hidden units | Value Unit (MTA) | Recruitment (MRA) | Binary (MTB) | |||
| (M) | N = 5 | N = 10 | N = 5 | N = 10 | N = 5 | N = 10 |
| 1 | 19.49 | 34.90 | 19.01 | 34.92 | 9.53 | 8.58 |
| 2 | 35.16 | 36.89 | 27.07 | 36.86 | 26.17 | 39.63 |
| 3 | 36.96 | 39.52 | 26.30 | 37.67 | 59.18 | 39.64 |
| 4 | 39.71 | 39.41 | 24.93 | 36.97 | 54.85 | 47.95 |
| 5 | 37.80 | 39.82 | 27.53 | 39.15 | 61.06 | 53.79 |
| 6 | 37.12 | 37.49 | 32.84 | 38.99 | 45.60 | 60.18 |
| 7 | 41.27 | 38.69 | 29.31 | 39.36 | 13.87 | 51.94 |
| 8 | 39.14 | 41.83 | 25.98 | 39.49 | 33.11 | 55.74 |
| 9 | 35.36 | 40.51 | 29.49 | 42.84 | 32.23 | 61.67 |
| 10 | 37.19 | 38.74 | 28.22 | 40.24 | 48.94 | 61.60 |
| m | 35.92 | 38.78 | 27.07 | 38.65 | 38.45 | 48.07 |
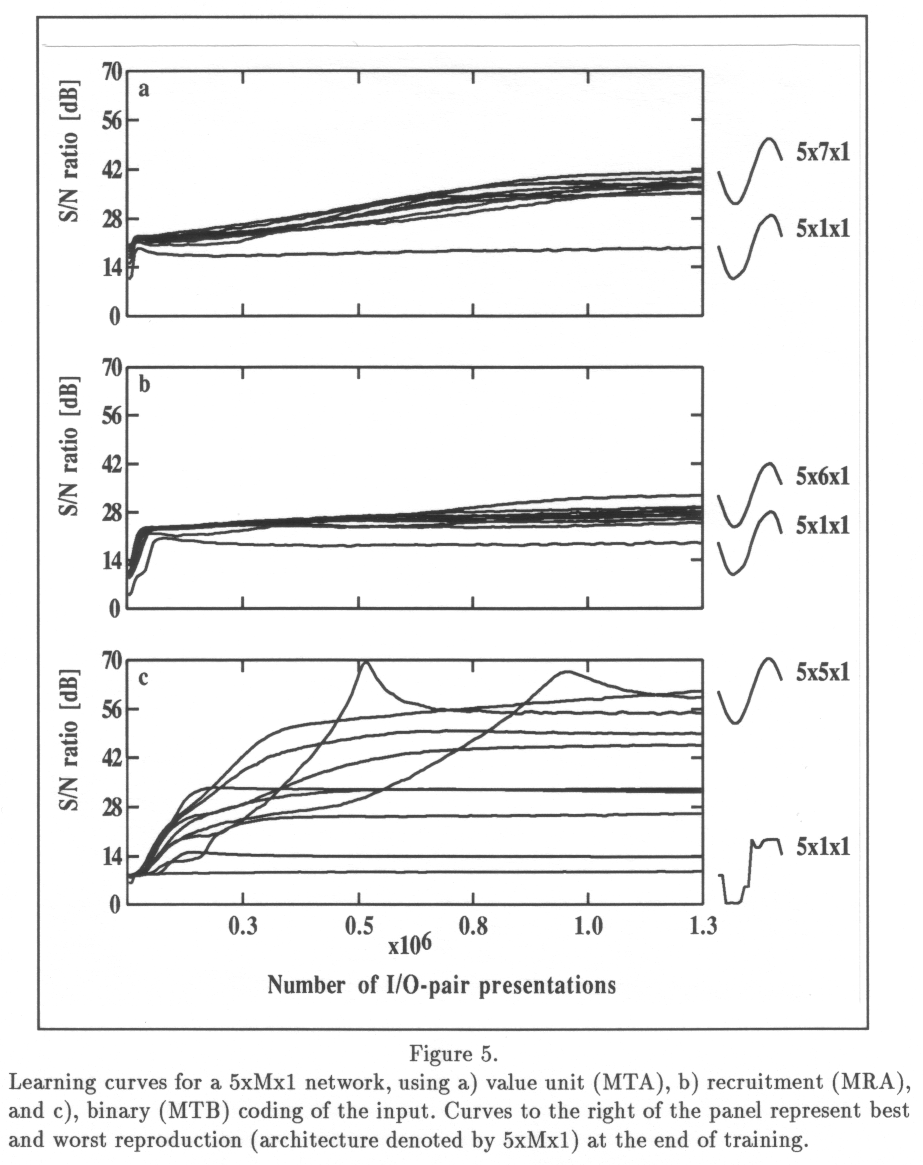
Figure 5 shows the learning curves for the 5xMx1 networks, displaying a steep rise in the signal to noise ratio during the initial 3x105 input/output presentations (16000 epochs), for all coding schemes. The value unit (MTA) coding scheme displays a steeper rising learning curve during the continued training. For all schemes, back propagation may occasionally fail to maintain an optimum representation, as evidenced by peak values in the learning curve exhibiting a higher signal to noise ratio than the value attained at the end of training if the number of units is inadequate. It should be noted that the number of presentations is much higher than in most other studies on back propagation, and that single-precision floating point operations were used. At other times, back propagation manages to recover from such "catastrophes". Figure 6 shows the learning curves for the 10xMx1 networks. It can be seen that the learning curves are much more regular, also in the case of binary coding. Figures 5 and 6 also give clues concerning the learning speed. Value unit coding (MTA) initially learns fastest, followed by recruitment coding (MRA). Learning a binary representation is relatively slow and less well-behaved. Table shows the signal to noise ratio after 120000 presentations of input/output pairs (6316 epochs). This point is at about one third of the point where most learning curves are flattening and at about one tenth of the total training duration. Here, the initial difference between value unit and recruitment coding virtually disappears, binary coding still displaying lowest values. Networks with a number of hidden units M = 10 learn faster than in case M = 5.
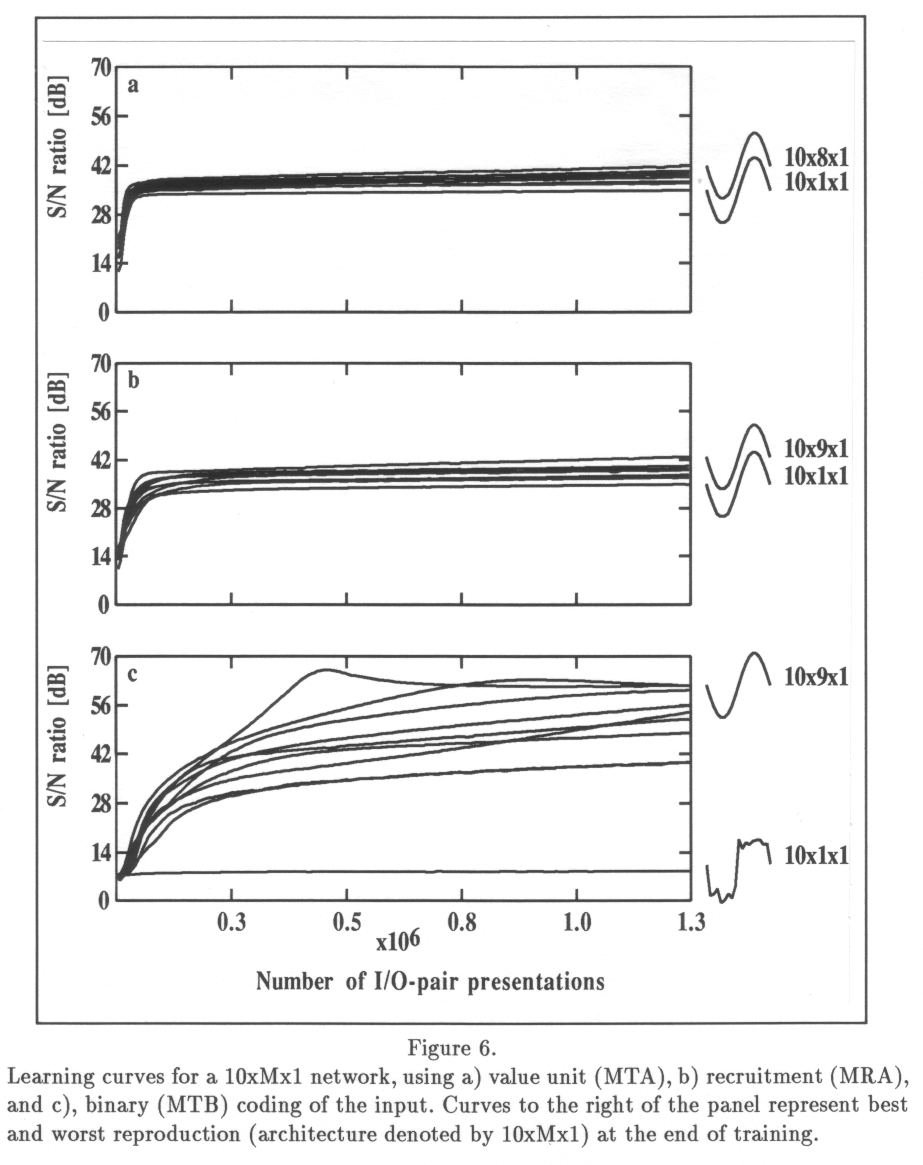
| Value Unit (MTA) | Recruitment (MRA) | Binary (MTB) | ||||
| N = 5 | N = 10 | N = 5 | N = 10 | N = 5 | N = 10 | |
| DS/N, at 0.1xT | 21.88 | 36.19 | 23.05 | 35.69 | 20.20 | 27.42 |
| DS/N, at T | 35.92 | 38.78 | 27.07 | 38.65 | 38.45 | 48.07 |
| % | 60.91 | 93.32 | 85.15 | 92.34 | 52.54 | 57.04 |
4 Discussion
The decreasing accuracy of the input/output mapping in case of increasing M in an NxM or 1xM network is most probably due to the collinearity problem. Since all output units are equipotential in terms of their plasticity, an infinite number of solutions (combinations of weight and threshold values) is possible. Also, the 1xMx1 architecture is limited with respect to the level of obtainable accuracy. For this latter case, i.e., the Single-unit Activation or rate coding, it can be predicted that in a non-linear mapping, a biological single-unit receptor needs a bundle of fixed, (non-plastic) connections to an intermediate layer containing a large number of units. This constraint is used in network models by Kanerva (1988).
In the NxMx1 networks, stable learning occurs if the number of units used in the input encoding is sufficiently high. In value unit (MTA) and recruitment (MRA) coding, the adding of hidden units only has a marked effect on the accuracy as long as the general shape of the output function has not been reached. After that point, improvements are marginal. Binary coding (MTB) is very sensitive to the number of hidden units. In the current experiment, the presence of hidden units NxMx1 was needed to obtain a good binary mapping. Potentially, this scheme may yield a high accuracy, but the unpredictable learning behavior may be one of the reasons that prevented its natural evolution in biological systems. Value unit encoding leads to faster initial learning by a multi-layer perceptron than recruitment coding, in terms of the absolute error. However, recruitment coding is faster in terms of reaching the plateau of the signal-to-noise ratio in case of a small (N=5) number of units. Value unit encoding has an advantage in terms of accuracy when only a small number of units is used.
The differences between value unit and recruitment coding as applied in the teaching of a non-linear function to a multi-layer perceptron are small. Results seem to indicate that in case of a limited number of input units (5) the value unit scheme has a slight advantage in terms of accuracy and the recruitment scheme has an advantage in terms of learning speed. If a larger number of units is used (10) this difference disappears. However, there may be other grounds for choosing a particular coding scheme. If the behavior of single units is noisy, as in the biological neuron, it can be predicted that recruitment coding is much more robust, and therefore a better choice. With respect to the modeling of handwriting, the results indicate that for the coding of a quantity (e.g., displacement), the learning of a non-linear relation is easier the more input units are used in a value unit or recruitment scheme. Using a single input neuron and rate coding, delegating the solution of the non-linear mapping to the hidden units is more difficult than using multiple input neurons. Findings (NxM studies) also indicate that it is advantageous to reduce the number of units representing the output range, relative to the number of units in the preceding layer. It can be hypothesized that the high proportion of biological neurons having a large fan-in/fan-out ratio (Crick & Asanuma, 1987) is related to their ability to represent a non-linear mapping of the input domain by dendritic topology.
5 References
Agarwal, G.C., & Gottlieb, G.L. (1975). An analysis of the electromyogram by Fourier, simulation and experimental techniques. IEEE Transactions on Biomedical Engineering, 22, 225-229
Ballard, D.H. (1986). Cortical connections and parallel processing: Structure and function. Behavioral and Brain Sciences, 9, 67-120.
Blinowska, A. Verroust, J., & Cannet, G. (1979). The determination of motor units characteristics from the low frequency electromyographic power spectra. Electromyography and clinical Neurophysiology, 19, 281-290.
Crick, F., & Asanuma, C. (1987). Certain aspects of the anatomy and physiology of the cerebral cortex. Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Volume 2 Psychological and Biological Models (pp. 334-389). Cambridge, MA: MIT Press.
De Luca, C.J. (1979). Physiology and mathematics of myoelectric signals. IEEE Transactions on Biomedical Engineering, 26, 313-325.
Gielen, C.C.A.M., & Coolen, A.C.C. (1989). Self-organization in neural networks underlying the coordination of movements. In J. Schopman (Ed.), Publications Series. Vol 24. Utrecht: The department of epistomology and philosophy, Utrecht University (The Netherlands)
Hinton, G.E., McClelland, J.L., & Rumelhart, D.E. (1986). Distributed representations. In J.L.McClelland, D.E. Rumelhart and the PDP research group (Eds.), Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Volume 1 Foundations (pp. 77-109). Cambridge, MA: MIT Press.
Kanerva, P. (1988). Sparse Distributed Memory. Cambridge (MA): MIT Press.
Lago, P., & Jones, N.B. (1977). Effect of motor unit firing time statistics on EMG spectra. Medical & Biological Engineering & Computing, 15, 648-655.
Milgram, P., & Inbar, G.F. (1974). Multichannel information transmission in the nervous system. In G.F. Inbar (Ed.), Signal analysis and pattern recognition in biomedical engineering (pp. 289-321). New York: Wiley.
Pellionisz, A.J. (1986). Old dogmas and new axioms in brain theory. Behavioral and Brain Sciences, 9, 103-104.
Rumelhart, D.E., Hinton, G.E. & Williams, R.J. (1986). Learning internal representations by error propagation. In J.L.McClelland, D.E. Rumelhart and the PDP research group (Eds.), Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Volume 1 Foundations (pp. 318-362). Cambridge, MA: MIT Press.
Van Boxtel, A., & Schomaker, L.R.B. (1983). Motor unit firing rate during static contraction indicated by the surface EMG power spectrum. IEEE Transactions on Biomedical Engineering, 30, 601-609.
Chapter 7
Neural Network Models of Temporal Pattern Generation
Lambert R.B. Schomaker
Abstract
Most contemporary neural network models deal with essentially static, perceptual problems of classification and transformation. Models such as multi-layer feedforward perceptrons generally do not incorporate time as an essential dimension, whereas biological neural networks are inherently temporal systems. In modeling motor behavior, however, it is essential to have models that are able to produce temporal patterns of varying duration and complexity. Several representations of time are dealt with, i.e., spatialized (topological) time models, temporal flow models, and recurrent networks. An alternative model is proposed, based on a network of pulse oscillators consisting of neuron/interneuron (NiN) pairs. Due to the inherent temporal properties, a simple NiN net, taught by a pseudo-Hebbian learning scheme, is able to display repetitive behavior which is much harder to teach to static non-pulse models. Two network models, a recurrent net and a pulse oscillator net are compared, using the simulation of pen-tip movement in handwriting as a common reference.
1 Introduction
The production of complex patterns of activity along several dimensions is probably the most intriguing aspect of motor control. However, it is also a most difficult problem to tackle since we do not currently have sufficient insight in the functionality and architecture of the neural systems that provide for motor control. There exists a long and fruitful tradition of measuring physiological parameters in detailed parts of the nervous system, but it is hard to integrate the vast amount of empirical detail into a more general theory. Therefore, a viable approach may be the creation of models that are based upon general electrophysiological mechanisms of single cell behavior, trying to find an architecture which is able to display a known functionality in motor behavior. The goal of the current paper is to describe possible general, neurally inspired, mechanisms for the production of complex but smooth multi-dimensional motor patterns, as opposed to the production of discrete-element sequences. Other functions in motor control like sensory feedback and inverse kinematics or kinetics computation (the degrees of freedom problem) are not considered here. Neither are mono-phasic targeting movements, as described in models by Bullock & Grossberg (1988) or by Houk et al. (1989). The central issue here is the generation of patterns.
The origin of a movement pattern
Traditional reaction time oriented studies in cognitive psychology did not concern the ïnternals" of the motor system. In cognitive motor theory, the production of a pattern is reduced to an abstract buffering and release of symbolic entities by an information processing system which is assumed to operate much like a computer (Sternberg et al., 1983; Schomaker et al., 1989). On the other hand, purely cybernetical or system-theoretical accounts explain only servo-like control without explicitly specifying where the ßet-level" or target time functions originate from. Only completely sensor-ruled behavior can be explained in terms of feedback alone. In his "closed loop" approach, Adams (1971) uses the additional abstract concept of memory trace to describe the origin of movement patterning. Although the non-linear dynamics as used in synergetics (Gibsonian motor theory) has an advantage in terms of the potential complexity of motor patterns that can be described in their kinematical and kinetical aspects, the latter theory fails to account for the concatenation of movement segments 9. Transitions between oscillatory modes of behavior are not completely explained by the bifurcation phenomenon (Parker & Chua, 1987a; 1987b) as a "deus ex machina" mechanism, because also here, the ultimate origin of the parameter change leading to the new global system state must be identified. In the case of long-duration pattern production such as in handwriting, it is more parsimonious to assume the existence of internal "motor representations" for movement segments that are fluently concatenated during execution, than it is to try to model longer sequences by complex and numerically vulnerable differential equations. An example is an oscillatory handwriting model by Hollerbach (1981). From the synergetics point of view, it is attractive, being an autonomous mass-spring oscillator model. On the other hand, it needs 13 parameters, and the model unrealistically assumes (Hulstijn & van Galen, 1983; van Galen et al, 1986) that writers plan words as a whole in advance. Also, there is more to motor behavior than oscillatory movement. It is useful to make a distinction between (a) models that describe the chaining of basic movement segments, and (b) models that describe the shaping of an individual movement segment. This distinction is not sharp and depends on the definition of "movement segment". The solution is to classify a given model as a chaining or shaping type model by asking the question how the model would handle the extreme case of very long-duration patterns vs its handling of details at a short time scale ( < 100ms). The shaping functionality typically requires implicit knowledge of the biomechanics of the output system, yielding neural activity that compensates for unwanted biomechanical side effects or making effective use of the properties of the output device. Hierarchically, shaping is of a lower level than chaining, i.e., a chaining module drives a shaping module. The distinction between chaining and shaping becomes evident in handwriting, where overlearned basic patterns (allographs) are chained into fluent movements. Also in speech, the occurrence of coarticulation effects can be described as shaping being influenced by the chaining process. Anticipation and perseveration errors in handwriting, typing, and speech indicate problems in the chaining process itself.
In order to develop a neurally inspired model of motor control that explains both chaining and shaping functionality, more study is needed. Below we will discuss how the time dimension is incorporated in current artificial neural networks, and see if and how different models can display the chaining or shaping functionality that are required in motor control.
Time in neural network models
Time is relevant to several aspects of neural network modeling. In the first place, it is of importance in the learning phase. For instance, teaching an input/output relation to a multi-layer network by back propagation (Rumelhart, Hinton, & Williams, R.J., 1986) generally takes hundreds of iterations. In the second place, time plays an important role in the operational phase of a network. How much time is needed to produce valid output values after presentation of an input pattern? In most multi-layer network models this time is fixed, assuming parallel "computation" by all the units, using an amount of time which is independent of the complexity of the relation between input pattern and output pattern. Obviously, this is not in agreement with behavior of the biological systems, as witnessed by a host of reaction time studies (Sternberg et al., 1983). Thus, the multi-layer perceptron models as such do not seem to incorporate time as a natural dimension. In this respect, Hopfield nets (Hopfield, 1982) and Boltzmann machines (Hinton & Sejnowski, 1986) display more correspondence with the biological neural networks because here, the duration of their relaxation is indeed dependent on the stimuli. However, the duration of the relaxation phase in the Boltzmann machine can be quite long, even if fast and parallel computing units are used, and the response time cannot easily be predicted on the basis of pattern complexity.
Unfortunately for students of motor control, most artificial neural network models ignore some essential features of biological networks that are related to time. Biological neurons are pulse oscillators, producing action potential trains by a stochastic point process, whereas artificial neurons as used in a perceptron are mostly only level reservoirs. Apart from specific physiological modeling studies, there is a limited number of general network models based on pulse oscillators (Torras i Genís, 1986; Peretto and Niez, 1986; Hartmann and Drüe, 1990; Tam and Perkel, 1989), and Von der Malsburg (1988). Also usually ignored is the fact that connections between units in a biological neural network imply transmission delays, the duration of which is determined by inter-unit distance and diameter of the axons. Typical axonal delay values are 8 ms/m to 1700 ms/m (Grossman, 1973). Other criticisms with respect to artificial neural networks exist (Crick & Asanuma, 1987), e.g., the limited Fan-out/Fan-in ratio in the neocortex as opposed to the connectivity demands of the fully interconnected artificial nets that are often used.
Spatialized representations of time
The denial or omission of the inherent temporal characteristic which biological networks possess, has sometimes lead to odd multi-layer models for the recognition of sequences of patterns, as noted by Stornetta et al. (1987). In these models, time is represented by columns of input units, one column per time step, for a fixed number of time steps. Network models of this type can thus be described as a more complex form of tapped delay lines10. Apart from the disadvantage in terms of the number of units if long sequences are to be recognized, the main shortcoming of such a system is its inadequate representation of patterns of varying length. Also, since the time steps are fixed, these models cannot handle temporally "jittering" input patterns either. An example of a speech recognition network where time is ßpatialized", i.e., represented topologically, is the TRACE model by McClelland and Elman (1986). A well-known model for the production of temporal patterns, i.e., keyboard typing, is given by Rumelhart & Norman (1982). This model, originating from work by Estes (1972), is also based on spatialized time, but the topology and the connectivity of the network is pre-structured by a planning agent. A sequence of discrete motor actions, key strokes, in time is produced by activations in an explicitly structured chain of units. A unit in this chain inhibits activity in all its successors until it has fired, thereby inducing a fixed sequential order, that occasionally may be disrupted by noise, as in real human typing. This model is a precursor to contemporary neural network modeling enterprises in cognitive science. Actually, the model is still of a hybrid nature since it contains a symbolic parser which parses a letter sequence and transforms it into a so-called key press schema. The key press schema is in fact a highly structured ßpecial-purpose" network which is geared to perform the key strokes in sequence. Although the model is very original and describes several phenomena also occurring in human typing there are some problems with it. First, the model describes discrete-time, discrete-value pattern production as opposed to continuous time, continuous value pattern production. Second, its highly structured architecture involves both activation and connectivity specification of movement segments in the "programming stage". Although connectivity specification is possible in principle by using multiplicative synapses in a neural network model, the original paper does not describe such structuring. Third, it is unclear how such a system should be trained. Fourth, inspection of figure 4 (Rumelhart & Norman, 1982, p. 17), which displays activation levels during a typing sequence, will reveal the susceptibility of the design to noise and the importance of fine threshold tuning. And fifth (Jordan, 1985), without specific modifications, the general architecture is not able to produce repetition of a given action unit. Consecutive repetition, e.g. AA is represented by a specific doubling action unit influencing the next action which follows. Alternation ABA can be solved similarly. But the model really comes into trouble when repetition over longer serial position differences must occur (ABCA), in which case the sequence must be broken up into e.g. ABC-A by a parser. As we have noted in handwriting, however, writers experience problems in correctly reproducing longer sequences of cursive 's and 's, e.g., at a normal writing speed, which indicates that humans also have trouble producing repetition of identical patterns (Schomaker et al., 1989), an argument which may be in favor of the Rumelhart & Norman (1982) chaining type model with unique context-free representations for each motor segment and a limited temporal scope.
Gradually, the importance of a more general and flexible representation of time is gaining recognition. Instead of considering, e.g., transmission delays as a nuisance which increases computational complexity, use can be made of their special properties, thus turning a liability into a virtue. Furthermore, the use of recurrent connections such that the state of a network at time t is influenced by the activation states of the units at time t-Dt offers a wide range of behaviors that are absent in the feedforward architectures. Notably, the variable-length sequence problem and the temporal jitter problem in speech and handwriting recognition could potentially be solved by recurrent network architectures (Robinson, 1989; 1990). In what follows we will describe shortly some network models which make no use of pre-structured spatialized time representations.
The temporal flow model
In multi-layer networks, Watrous & Shastri (1987) developed a so-called "temporal flow" model for recognition purposes: transforming a temporal signal into a static representation. The basic characteristic of such a network is that, contrary to the standard multi-layer perceptron architecture, single units have auto-recurrent links. A network like this is somewhat less sensitive to small time axis deviations than is the case in topological coding of time. The recurrent connections impose a "capacity" or first-order recursive filtering on the unit activation. The attractiveness of the temporal flow model lies in the fact that temporal information is handled by the distributed single-unit dynamics. In order to train such a network, a modified back propagation rule was given, which takes into account the unit activations over a short time window preceding time t in the input and target time functions. Watrous & Shastri (1987) taught the network to discriminate between two 16-channel time functions containing the spectral content for the spoken words "no" and "go". As the target output function, a ramp function was chosen which increases for the output unit corresponding to the required response and decreases for the non-matching unit. This representation was chosen under the assumption that a listener continuously builds up evidence for the detection of a specific word.
The temporal flow model can also be used as a production model, transforming a static representation or a short seed sequence into a (longer) temporal signal. Rumelhart, Hinton & Williams (1986) describe a model of the production of discrete sequences of patterns by a 3-layer network with recurrent loops within the hidden layer and within the output layer. The connections between layers are feedforward only. The idea is to feed the system with an initial seed pattern, which initiates a path through the state space, such that the activation of the output units in time is a completion of the total (taught) pattern. As an example, after having learned the sequences AA1212 and BA2312, presenting AA to the network should lead to the subsequent successive output states 1,2,1 and 2. A network of this type is claimed to handle fixed time step inconsistencies as well, after the proper amount of training. With respect to modeling motor behavior, the model relies on a discrete-value representation and is more a chaining type model than it is of the shaping type. A large amount of training is required to capture even these relatively simple patterns. Both in recognition and production, the complexity of patterns is limited by the first-order characteristics of the single units, which also puts a limit on the complexity of the pattern which can be produced by the network as a whole. Using higher-order transfer characteristics for the single units will allow for more complex ïmpulse responses" to be generated by such models in production and to capture higher-order dependencies between the system states at different points in time in recognition, than is the case with the first-order recurrent links. Theoretically, the temporal flow model can thus be used in shaping and chaining.
Recurrence in fully interconnected single-layer networks
By allowing transmission delays between units in a Hopfield network, Coolen and Gielen (1988) were able to store a number of sequences of binary patterns in such a net, provided that p << N where p is the number of patterns and N is the number of units. Williams & Zipser (1988) developed a learning algorithm for a network consisting of a single layer of fully interconnected units. Part of the layer receives input from the outside world, another part of the layer consists of öutput" units whose behavior must follow some time function based on the initial inputs. This network can learn some interesting dynamic behaviors like delayed XOR mapping, parenthesis matching or sinusoidal oscillation. A pervasive problem in training these recurrent networks is the often slow learning speed and the inability to escape from non-optimal solutions. To solve this problem, special (less general) versions of learning rules exist. With respect to motor models, it is as yet unclear how fruitful the idea of fully interconnected single-layer networks will be with respect to the chaining and shaping aspects in motor control. Recurrence in multi-layer perceptrons
Jordan (1985) developed a framework for the production of sequences by trainable recurrent multi-layer perceptrons. In this type of networks, the input layer consists of externally driven connections for the selection of learned sequences combined with connections representing the network's (previous) output state. Jordan was able to model limited, variable length sequences containing repetitions and alternations (AA,AABB,AABA,ABAC,ACABAA). These sequences are of a discrete-value, discrete-time nature. The longer the sequence, the longer the teaching phase lasts. Other experiments include speech production where coarticulation effects could be modeled using this architecture. In the latter case, the patterns consist of activations for different speech features, and are of a continuous value, discrete-time nature. Interesting properties of this model are the trainability, the distributed representation of the temporal system state and the natural inclusion of "coarticulation" effects. This models seems to combine chaining and shaping functionality.
A pulse oscillator ensemble model
A question which may be asked is: "why try to model temporal behavior using static cells if nature itself has come up with an inherent temporal system: the neuron as a stochastic generator of action potentials in time"? Why not consider biological networks as complex systems of oscillators and resonators? Indeed, oscillators and resonators potentially offer interesting capabilities like entrainment, synchronisation, complex pattern generation and completion by resonance (cf. Hebb's cell assemblies), that their static perceptron-like counterparts do not have (Eckhorn et al., 1988; Skarda & Freeman, 1987). The problem with respect to modeling is that there exists no robust training mechanism for dynamical pulse oscillator networks, comparable to back propagation (PDP group), the learning rules developed by Grossberg (Carpenter & Grossberg, 1987), or Kohonen (1987). But there are other arguments in favor of more physiologically oriented models. The mechanism of motor unit recruitment (De Luca, 1979; Van Boxtel & Schomaker, 1983) reveals how a neural pulse oriented system can escape from the limited information capacity (Ballard, 1986) that a single axon suffers from. By a combined recruitment & firing rate control, a neural system can easily implement non-linear mappings that are required in a given Input/Output mapping problem. An interesting trainable pulse oscillator model is given by Torras i Genís (1986) who tried to teach neurons to fire at a given frequency. The learning rule consists of a dual process: the average membrane potential being incremented to increase the firing frequency if the cell is being activated often, and decrementing the average membrane potential if a depolarization occurs prematurely within a time window after the afferent driving neuron has fired.
Taking for granted the oscillatory behavior of neurons, it can be hypothesized that pattern generation, i.e., shaping, can be brought about by the selective combination of neural activity in a large ensemble of neurons. This hypothesis is similar to the Fourier-based composition of a signal. The main differences are that in this proposed model, the constituent candidate oscillator frequencies & phases are not in any way distributed evenly along the frequency & phase axis and that the signal shape is not sinusoidal. The phase relationship between the oscillators, however, may be constant if interconnections or a common triggering source exists. Also, the oscillators do not have to fire at a constant frequency, emitting evenly distributed pulses. In fact, the envisaged system may profit from the fact that the neuron ensemble contains a rich set of non-linear oscillators to capture a wide spectral range without requiring subtle distributions of fixed frequencies.
A simple and basic mechanism to modulate oscillatory behavior of neurons is the mechanism of Neuron-inhibitory Interneuron (NiN) interaction (Figure 1) which is widely present at several levels of the central nervous system (Sloviter & Connor, 1979; Pratt & Jordan, 1979). Without claiming that this mechanism is the only or even the most important mechanism in producing complex spiking patterns, it is striking to see the variety of patterns that can be produced by a NiN pair of neurons (Figure 2). If the recurrent inhibition is weak, the NiN behaves almost as a normal single neuron. Depending on the parameters of the NiN pair, responses like delayed burst, single delayed discharge and grouping of spikes kan be obtained. Figure 3 shows the configuration of an ensemble of NiN oscillators and their connection to (two) output lines through a trainable weight matrix.
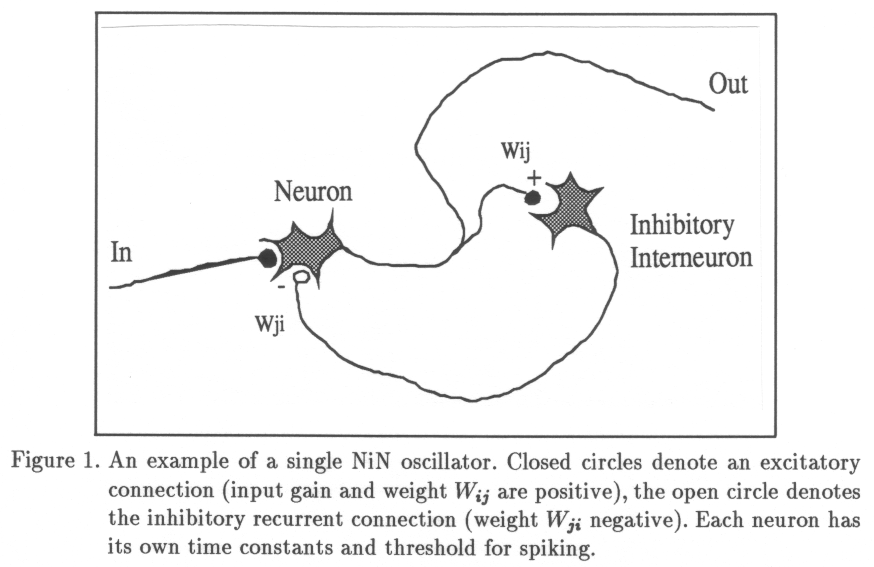
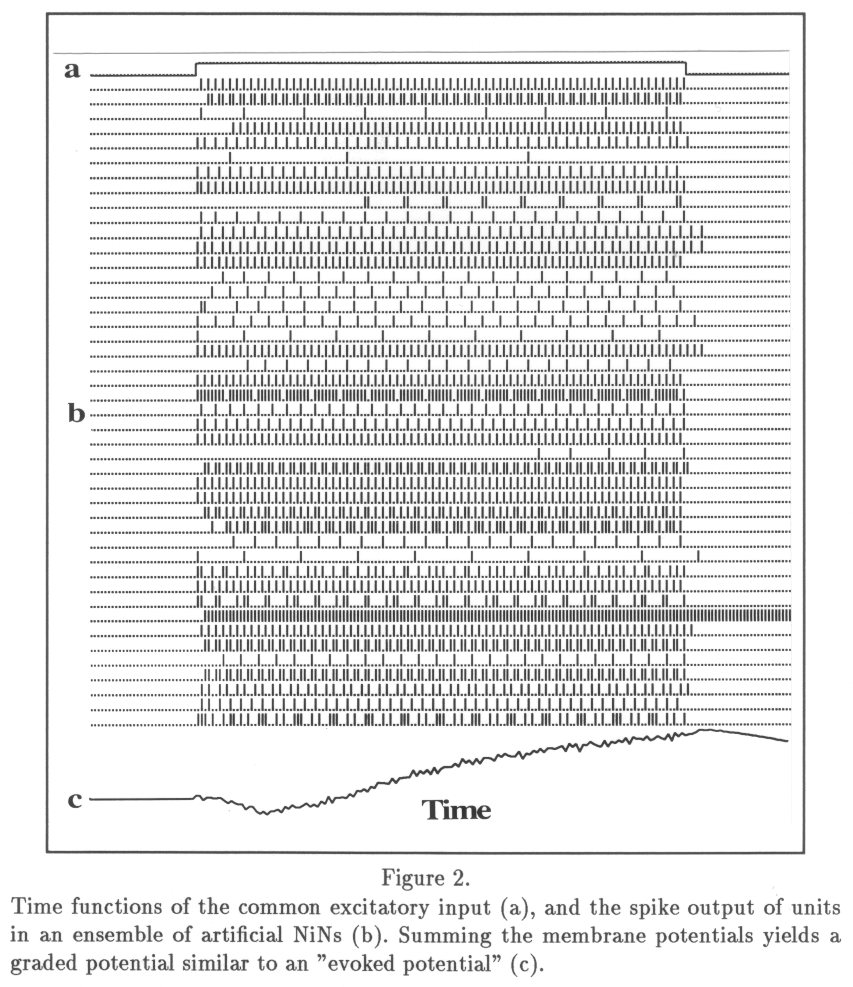
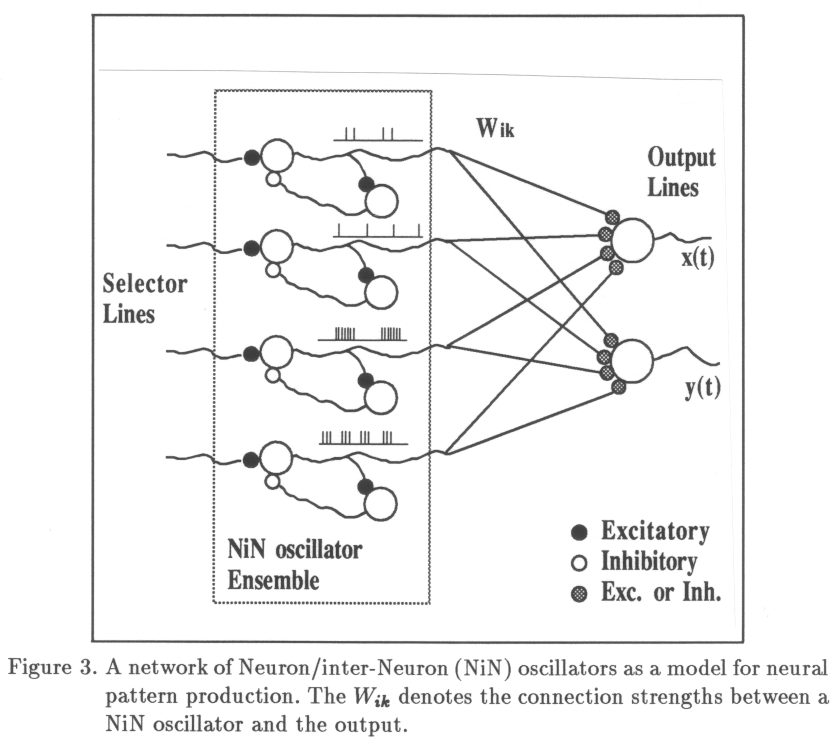
At this point, it appears interesting to compare the recurrent perceptron model with the proposed pulse oscillator model. How fast do they learn, how accurately are patterns reproduced, and how sensitive are they to intrinsic noise? Before describing two experiments, however, it is necessary to outline a common functionality that any pattern generator must be able to display.
General features needed in a motor pattern production system
In the production of motor patterns, four basic events or phases can be identified, both in chaining and in shaping:
- System Configuration.
- Start of Pattern.
- Execution of Pattern.
- End of Pattern.
System configuration.
This stage is known as motor programming,
coordinative structure gearing,
preparation, planning, schema build-up etc.11
It involves the determination of the pattern and the end
effector
system which is
going to be used. As a general model one may think of a list of binary values
representing a system configuration.
Start of pattern.
After configuring the system for the task at hand,
there must be a signal releasing the pattern at the correct time.
Execution of pattern.
The duration of this phase and the actions that are
performed depend on pieces of information such as the amount of time that has
passed, the distance from a spatial target position or force target value,
or even the number of motor segments produced. It can be hypothesized that
an incorrect representation or implementation of this stage leads to errors
as in stuttering and the counting problem in the production of strokes in
the cursive handwriting of m and w. An easy experiment is the
cursive writing of the word minimum without dots, keeping the eyes
closed, and writing at normal or slightly accelerated speed.
End of pattern.
There must be a signal or condition which identifies in
a non-ambiguous manner that the systems that are involved do not have to
be engaged in the production of the pattern any longer. The importance of
this signal is less clear from a pre-structured network like the timing
model of Rumelhart & Norman (1982), but it appears essential in recurrent
networks. Without special provisions, a recurrent
system which has learned
a repetitive pattern, say AABAAB, will go on producing this pattern unless
en external event signals the end of the pattern. Similarly, for non-repetitive
patterns, a recurrent network may indulge in
infinite chaotic babbling after
correctly reproducing a pattern. The same problem may occur in pulse oscillator
networks12.
There are basically two solutions to represent the Execution of pattern phase and the End of pattern event. First there is the autonomous solution, assuming a within-pattern relative time scale from which the current state can be derived. Second, there is the feedback-dependent solution, where sensory or efference-copy information is needed to determine the relative within-pattern phase or the end of the pattern (Bullock & Grossberg, 1988). Note that in the case of counting discrete events, e.g., the writing of strokes in 's or 's, the necessity of feedback becomes evident.
Finally, an important feature of a plausible neurally inspired model is that it should be able to tolerate a moderate amount of noise on the single unit activations.
We will now proceed to describe an experiment with two types of network models to perform the shaping task of individual letters in cursive handwriting, without describing their chaining into movement patterns encompassing a word.
2 Method
Experiment 1 concerns the training of Vx(t) and Vy(t) pen-tip velocity functions to a Jordan (1985) type network, modified to handle "continuous" functions. To achieve this, the output of a 3-layer network is coupled back to part of the input layer, providing for a recursive filter-like functionality by saving the last n output values produced in time, for each output channel. Note that this "tapped delay" is different from the spatialized time organizations in that n is no hard constraint on the maximum pattern duration. Apart from the delayed output information, the input layer is fed by a selector pattern (Figure 4).
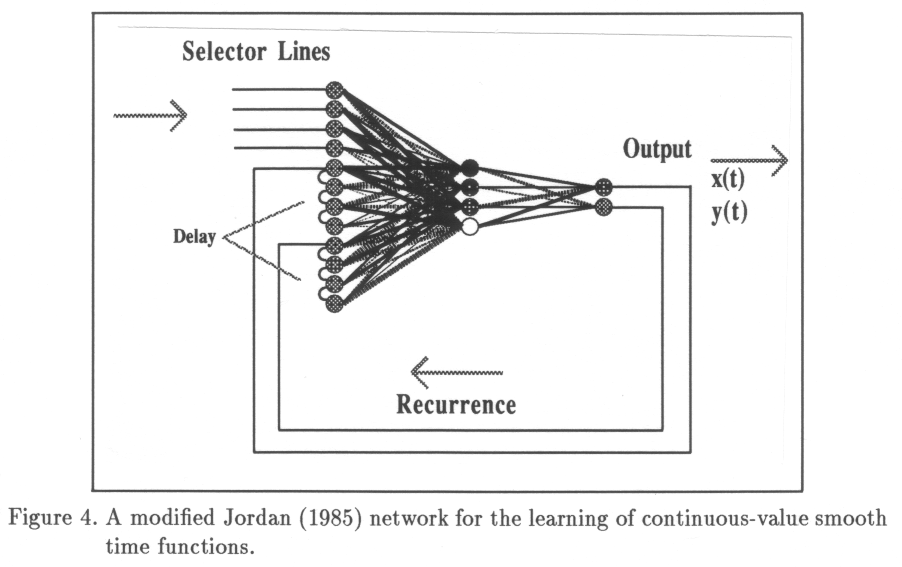
The System Configuration phase, which determines the movement pattern selection, is outside the model. The Start Pattern phase is signaled by a switch from relaxation (0.1) to maximal activation (0.9) of an input line which selects the movement pattern to be produced. To give the movement production model information about the within-pattern relative time during the Execute Pattern phase, the activation of the relevant selector line is exponentially decaying during the duration of the movement. Contrary to the schema for striking a key in Rumelhart & Norman (1982), there is no explicit signaling of the End of Pattern phase. The time constant of the decay is chosen such that the selector activation is lower than 0.2 at the end of the movement pattern. Training is done using a normal back propagation algorithm with this difference that instead of a momentum term the function W¢ij(n) = bWij(n) + (1-b) W¢ij(n-1) is used to separate effects of learning speed h from effects caused by the smoothing factor b. Single unit activation levels contained 0.1% added noise from a uniform distribution. The real-valued input and output variables were coded using a combined activation and position scheme ("flying spot", Chapter 6). The network structure was as follows. The output layer consisted of 2 output units for Vx and Vy. The input layer consists of 5 time delay taps for both channels, using 2 units per tap in "flying spot" coding, and a selector channel also using 2 units, yielding a total of 22 input units. There were 15 hidden units, which is less than the number of input units to enforce "generalization" or smoothing on the time functions. The selector channel was fed with an exponentially decaying signal. Relevant dependent variables are learning speed and the normalized rms error between target and produced patterns. Also investigated is the ability to store more than one pattern in a single network.
Experiment 2 concerns the training of X and Y pen-tip displacement functions to a pulse oscillator network of Neuron/Inter-Neuron pairs. The NiN pairs are mutually independent in the current version of the model. The parameters for the neurons are drawn from a uniform probability distribution and are not modified during training for this initial experiment. The System Configuration phase, which determines the movement pattern selection, is outside the model. The Start Pattern phase, Execute Pattern Phase, and End Pattern phase are determined by activating the Neurons of a set of NiN pairs, and releasing the activation at the end of the pattern (square wave). The firing behavior of each neuron (including interneurons) is governed by a general neuron model by Perkel et al. (1964, in Torras i Genís, 1986) (see Appendix). Training is achieved by use of an experimental training rule that is based on the correlation between single NiN activity and the error between target time function and obtained time function. The rule is non-local. In a sense, it combines Hebbian, or covariance learning, with the delta rule:
| (8) |
where Wik is the connection strength between a single NiN i and output line k, he is the learning speed, rei is the correlation between NiN oscillator i's activity ui(t) and the error time function e(t) = yk(t)-ok(t). The target function is yk(t), ok(t) is the output of line k, rg is the overall correlation between the output ok(t) and the target yk(t). The squashing term ensures smaller weight changes, the more ok(t) approaches yk(t). Furthermore, Wik is smoothed, similar to the use of a momentum term in back propagation:
| (9) |
The common output ok(t) is the low-pass filtered (F), weighed sum of individual NiN spike outputs ui(t):
| (10) |
where k = 1 or k = 2 for the X and Y displacement target signals, respectively. Note that a single NiN i contributes to different output lines k. The low-pass filtering (cut-off frequency 10 Hz) is used to simulate a virtual "muscle" system (Teulings and Maarse, 1984).
Single unit activation levels contained 0.1% added noise from a uniform distribution. There is no between-NiN connectivity. The NiN parameters are unchanged in this experiment. They are drawn from a uniform distribution, bounded by "reasonable" extremal parameter values (Appendix). There were 400 NiN oscillators, he = 0.1, a = 0.02
In both experiments, the training sets consist of the pen-tip movement signals (X(t),Y(t) or Vx(t), Vy(t)) of isolated cursive characters of a single writer. The data were obtained using a Calcomp 9000 series digitizer, sampling at 100 Hz. The letters used here were manually isolated from whole words using a handwriting editor program. The beginning and end of a pattern were padded with zeroes (relaxed state) corresponding to a 50ms real-time duration. Neural network simulation software was written in Fortran-77 and simulations were executed on a VAXstation 2000 computer.
3 Results
Experiment 1. Training the recurrent network, using 2000 presentations of the Vx,Vy pattern of an , lasting .66s (66 samples) costs over 3 hours of computation on a VAXstation 2000. Figure 5 gives an overview of some training histories, (letters ) concerning the teacher-forced behavior. Figure 6 gives an overview of the training history, concerning the free running recurrent operation. Note the different scale of figures 5 and 6. The free-running mode of the network never showed a legible approximation of the handwriting in this experiment, and the learning history is irregular for and . Figure 7 shows a typical simulation result. Only the feedforward "teacher-forced" operation leads to a mimicking of the handwriting pattern. In the free-running operation, the pattern degenerates rapidly as a consequence of bias and the 0.1% noise imposed on the units. Figure 8a and b show similar results for an 18x10x2, 4-tap architecture after 4500 and 6000 pattern presentations, respectively. Only after over 10000 training trials, we were able to teach an to a recurrent network (Figure 8c). In this case the state space trajectory was robust, allowing for a 5% noise on the selector channel in the free run. However, in the latter case, 50% of the input units consisted of selector units, reducing the recurrent state influence on the trajectory evolution. Experiments with other letters from the alphabet produced very comparable results.
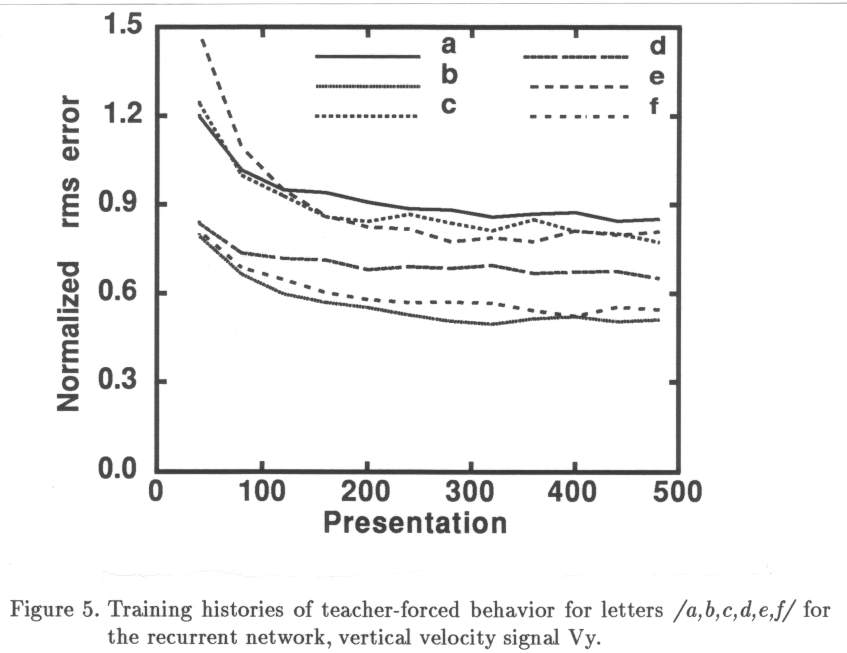
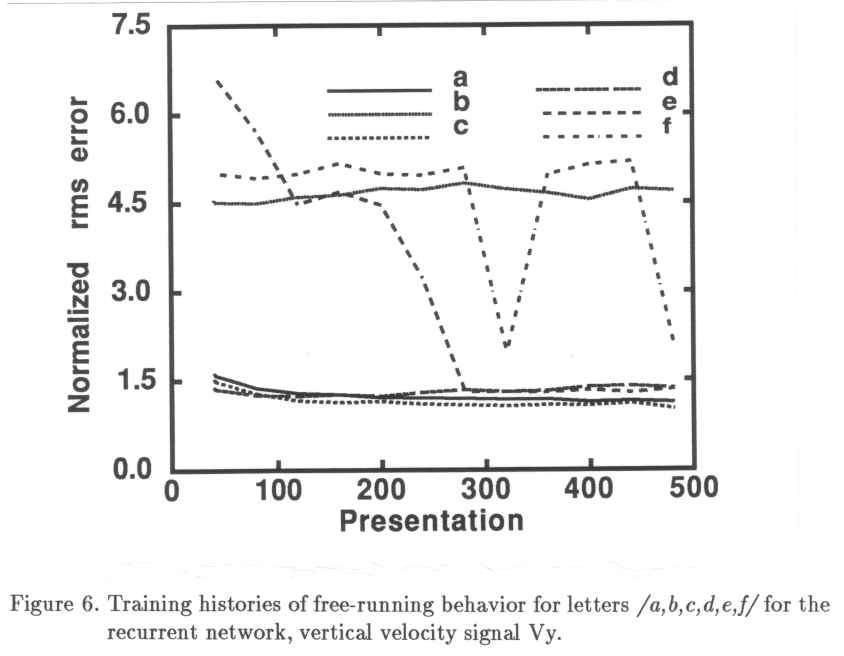
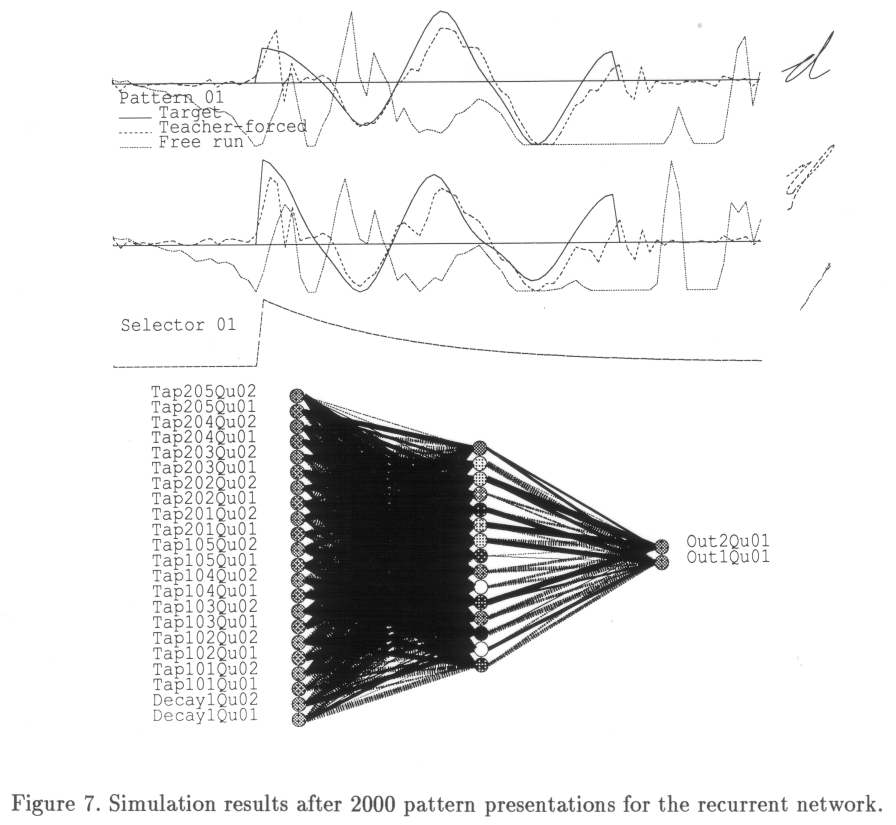
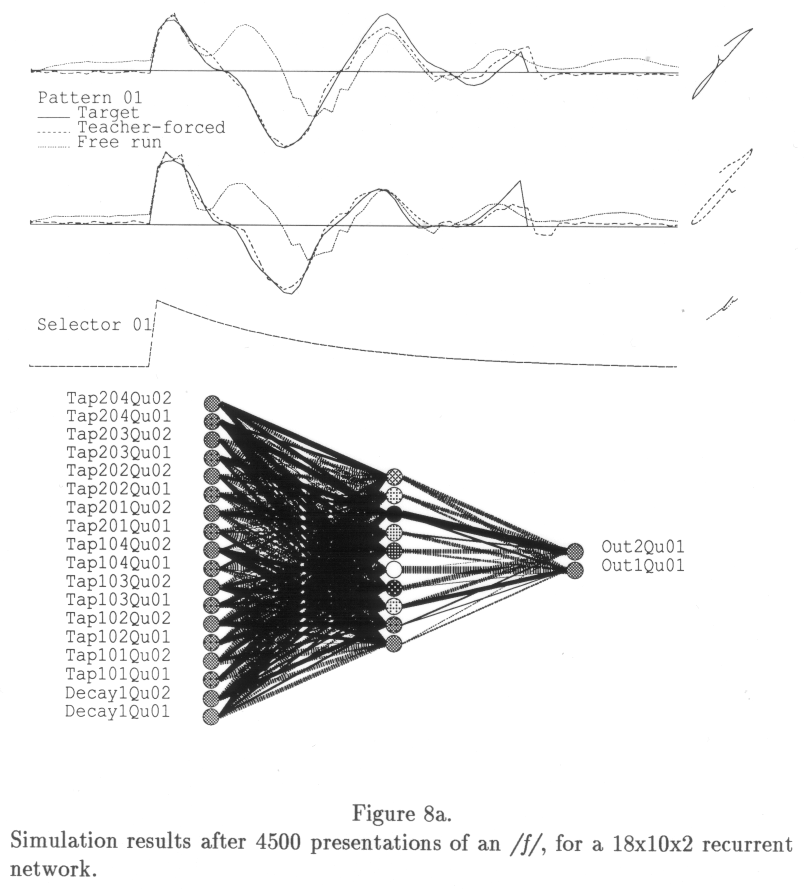
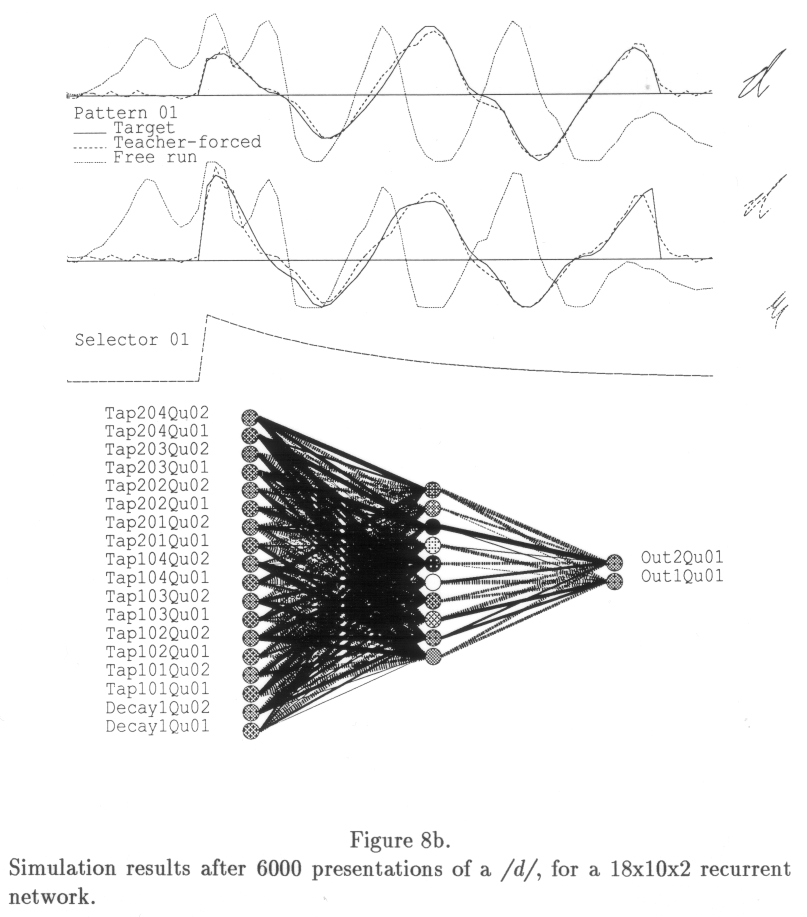
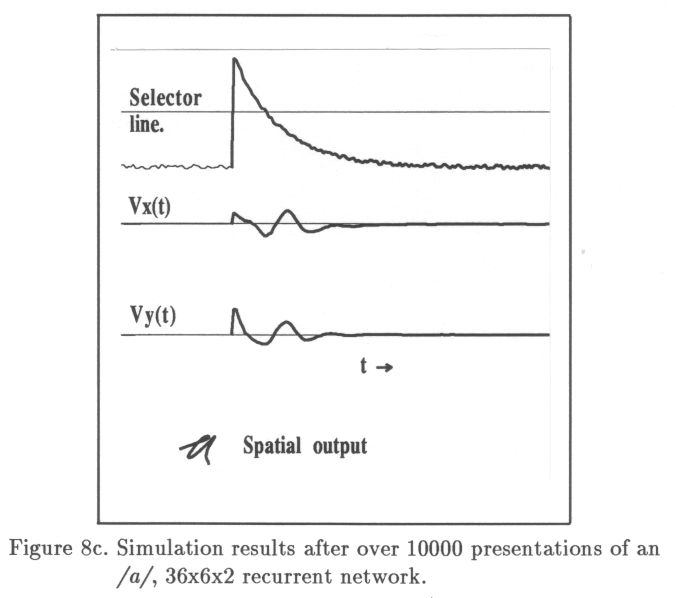
Experiment 2. Training the NiN network, using 500 presentations of the X,Y pattern of an , lasting .66s (66 samples) costs about 2 hours of computation on a VAXstation 2000. Figure 9 shows typical training histories for 6 cursive letters , reaching a flat learning curve after 300 presentations. However, the learning rule apparently does not always leads to convergence. The deviating is due to a failure in matching the Y-amplitude, while the shape of pattern is still approximated. This can be inferred from figure 10, showing the simulation results for the 6 letters. The amplitudes of X(t) and Y(t) output were normalized to the amplitude of the target pattern. The error is largest at the end of the pattern, due to the low-pass filtering of the output. In the a, the X(t) signal is only roughly approximated.
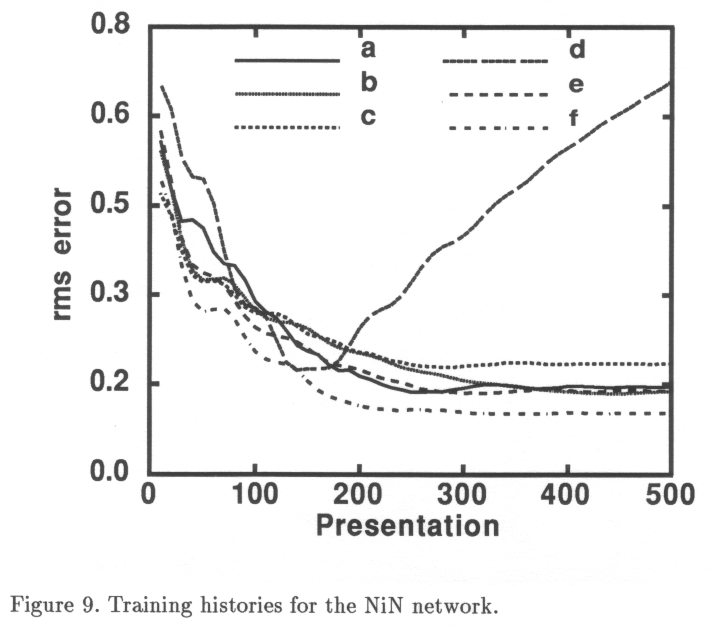

The NiN network performed better than the recurrent network, also for the teacher-forced operation, which can be inferred from the asymptotic normalized rms values in figures 5 and 9.
4 Discussion
A problem with the recurrent network is the degeneration of patterns in the free running state. This means that such an architecture will be strongly dependent on correct feedback to compensate for the internal errors and biases introduced at each time step. Whereas this seems a reasonable assumption in the case of discrete patterns (typing), it is not clear if this is true for the case of continuous patterns. In handwriting, visual feedback, at least, does not seem to be a primary factor in maintaining pattern integrity (van Galen et al., 1987). It should be noted that the findings are relevant to the used limited-sized networks only. Computational demands inhibit the experimentation with large-size networks. For example, it is to be expected that a larger number of units for an input variable in "flying spot" coding increases the robustness of the recurrent network. Although the recurrent multi-layer perceptron is an attractive model in its generality, it did not display a convincing "natural" functionality. The learning speed was very slow. Also, we were not able to store more than one pattern in a single recurrent network, which reduces its likelihood as being the basis for both chaining and shaping. Dedicated learning rules may alleviate these problems to some extent, but potentially introduce new degrees of freedom that may even be less realistic from the physiological point of view. Summarizing: the training of the recurrent network appears to be a "forcing" of an essentially static system to display temporal behavior. Although the general idea remains attractive, more study is needed in the field of the training of recurrent networks in general.
The NiN pulse oscillator ensemble model displayed a fast but uncertain learning behavior. The learning rule does not always lead to convergence. More analytical work is necessary in this field. The accuracy of the pattern reproduction depends on the distribution of the neuron parameters in the ensemble. In this experiment, the neuron parameters were unmodifiable. After dedicating a set of NiNs to a pattern through a weight matrix, fine tuning can be obtained theoretically by adapting the neuron parameters. To achieve this, learning rules similar to the one used by Torras i Genís (1986) have to be identified. Other interesting features of the NiN network are the natural oscillation and the influence of the general activation level on the average firing rate, allowing for pace modulation. One can predict that there will be a range in which the pace of a given pattern can be varied, breaking down outside the working range. Doubling of a movement segment can be produced by a single NiN oscillator. In this sense, doubling errors in typing can be modeled as the result of an increased drive on a group of NiN oscillators. Summarizing: the NiN network model may be a promising way of modeling motor behavior. Much more work is needed with respect to its physiological credibility, learning rules, and its capacities in terms of faithfully modeling motor parameter invariance. Obviously, any neural network model of pattern production in motor behavior should display a functionality that exceeds the mere storage and retrieval of a pattern.
5 Appendix
A neuron model by Torras i Genís (1986) is described as:While (Pb + Ps) < H, relax:
| |||||||||||||||||||||||
| |||||||||||||||||||||||
| Pb | spontaneous membrane potential |
| Ps | post-synaptic potential |
| H | firing threshold |
| x | input |
| y | output |
and the constants are:
| Pb0 | membrane potential directly after firing |
| Pb1 | asymptotic membrane potential in relaxed state |
| H0 | firing threshold directly after firing |
| H1 | firing threshold in relaxed state |
| tb | time constant of membrane potential |
| ts | time constant of post-synaptic potential |
| th | time constant of threshold change after firing |
A simplification yielding qualitatively the same type of
behavior is:
While (Pb + Ps) < H ÚPb > H0, relax:
| |||||||||||||
| |||||||||||||
| |||||||||
Here the threshold H remains constant. Input x = [0,1].
The latter type was used in experiment 2 as reported here.
A NiN pair is connected by:
| ||||||||||||||||||
where:
| x | external input to the NiN |
| xi | input to the neuron |
| xj | input to the interneuron |
| yi | output of the neuron |
| yj | output of the interneuron |
| wij | forward weight from neuron to interneuron |
| wji | recurrent weight from interneuron to neuron |
| y | NiN output |
Parameter range (uniform probability density function):
| Parameter | Min | Max |
| tb | 0.1 | 0.999 |
| ts | 0.0001 | 0.1 |
| H1 | 0 | 0.9 |
| H0 | 0 | 1 |
| Pb1 | 0 | 0.9 |
| wij | 0.01 | 2 |
| wji | -2 | 1 |
6 References
Adams, J.A. (1971). A closed-loop theory of motor learning. Journal of Motor Behavior, 3, 111-149.
Ballard, D.H. (1986). Cortical connections and parallel processing: Structure and function. Behavioral and Brain Sciences, 9, 67-120.
Bullock, D., & Grossberg, S. (1988). Neural dynamics of planned arm movements: Emergent invariants and speed-accuracy properties during trajectory formation. Psychological Review, 95(1), 49-90.
Carpenter, G.A. and Grossberg, S. (1987). ART-2: Self-organization of stable category recognition codes for analog input patterns Applied Optics, 26(23), 4919-4930.
Coolen, A.C.C., & Gielen, C.C.A.M. (1988). Delays in neural networks Europhysics Letters, 7, 281-285.
Crick, F., & Asanuma, C. (1987). Certain aspects of the anatomy and physiology of the cerebral cortex. Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Volume 2 Psychological and Biological Models (pp. 334-389). Cambridge, MA: MIT Press.
Eckhorn, R., Bauer, R., Jordan, W., Brosch, M., Kruse, W., Munk, M., & Reitboeck, H.J. (1988). Coherent oscillations: A mechanism of feature linking in the visual cortex? Biological Cybernetics, 60, 121-130.
Estes, W.K. (1972). An associative basis for coding and organization in memory. In A.W. Melton & E. Martin (Eds.), Coding processes in human memory. (pp. 161-190). Washington, D.C.: Winston.
Grossman, S.P. (1973). Essentials of Physiological Psychology. p. 28, New York: Wiley.
Hartmann, G. & Drüe, S. (1990). Feature linking by synchronization in a two-dimensional network. Proceedings of the IEEE International Joint Conference on Neural Networks 1990 Vol. I, 247-250.
Hinton, G.E. and Sejnowski, T.J. (1986). Learning and Relearning in Boltzmann Machines. In: J.L.McClelland, D.E. Rumelhart and the PDP research group (Eds.), Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Volume 1 Foundations (pp. 282-317). Cambridge, MA: MIT Press.
Hollerbach, J.M. (1981). An oscillation theory of handwriting. Biological Cybernetics, 39, 139-156.
Hulstijn, W., & Van Galen, G.P. (1983). Programming in handwriting: Reaction time and movement time as a function of sequence length. Acta Psychologica, 54, 23-49.
Hopfield, J.J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences, USA, 79, 2554-2558.
Houk, J.C., Singh, S.P., Fisher, C., & Barto, A.G. (1989). An adaptive sensorimotor network inspired by the anatomy and physiology of the cerebellum. In: W.T. Mille, R.S. Sutton, & P.J. Werbos (Eds.), Neural Networks for Control, Cambridge (MA): MIT Press.
Jordan, M.I. (1985). The learning of representations for sequential performance. Doctoral dissertation. University of California, San Diego, pp. 1-160.
De Luca, C.J. (1979). Physiology and mathematics of myoelectric signals. IEEE Transactions on Biomedical Engineering, 26, 313-325.
Kohonen, T. (1987). Adaptive, associative, and self-organizing functions in neural computing. Applied Optics, 26, 4910-4917.
McClelland, J.L., & Elman, J.L. (1986). Interactive processes in speech perception: The TRACE model. In: J.L.McClelland, D.E. Rumelhart and the PDP research group (Eds.), Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Volume 2 Psychological and Biological Models (pp. 59-121). Cambridge, MA: MIT Press.
Parker, T.S., & Chua, L.O. (1987a). Chaos: A Tutorial for Engineers. Proceedings of the IEEE, 75, 982-1008.
Parker, T.S., & Chua, L.O. (1987b). INSITE-A software toolkit for the analysis of nonlinear dynamical systems. Proceedings of the IEEE, 75, 1081-1089.
Peretto, P., & Niez, J.-J. (1986). Stochastic dynamics of neural networks IEEE transactions on systems, man, and cybernetics, 16, 73-83.
Perkel, D.H., Schulman, J.H., Bullock, T.H., Moore, G.P., & Segundo, J.P. (1964). Pacemaker neurons: Effects of regularly spaced synaptic input, Science, 145, 61-63.
Pratt, C.A., & Jordan, L.M. (1979). Phase relationships of motoneuron, Renshaw cell and Ia inhibitory interneuron activity periods during fictive locomotion in mesencephalic cats. Abstracts of the 9th Annual Meeting of the Society for Neuroscience, Vol 5, 728.
Robinson, A.J. (1989). Phoneme Recognition from the TIMIT database using Recurrent Error Propagation Networks. Technical Report 42, Cambridge University Engineering Department (UK).
Robinson, A.J. (1990). Dynamic Error Propagation Networks. Doctoral dissertation. Cambridge UK: University of Cambridge.
Rumelhart, D.E., & Norman, D.A. (1982). Simulating a skilled typist: A study of skilled cognitive-motor performance. Cognitive Science, 6, 1-36.
Rumelhart, D.E., Hinton, G.E. & Williams, R.J. (1986). Learning internal representations by error propagation. In J.L.McClelland, D.E. Rumelhart and the PDP research group (Eds.), Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Volume 1 Foundations (pp. 318-362). Cambridge, MA: MIT Press.
Schomaker, L.R.B., Thomassen, A.J.W.M., & Teulings, H.-L. (1989). A computational model of cursive handwriting. In R. Plamondon, C.Y. Suen, & M.L. Simner (Eds.), Computer Recognition and Human Production of Handwriting (pp. 153-177). Singapore: World Scientific.
Sejnowski, T.J. & Rosenberg C.R. (1986). Parallel Networks that Learn to Pronounce English Text, Complex Systems, 1, 145-168.
Skarda, C.A. & Freeman, W.J. (1987). How brains make chaos in order to make sense of the world. Behavioral and Brain Sciences, 10, 161-195.
Sloviter, R.S., & Connor, J.D. (1979). Effect of Raphe stimulation on granule cell activity in the hippocampal dentate gyrus. Abstracts of the 9th Annual Meeting of the Society for Neuroscience, Vol 5, 282.
Sternberg, S., Knoll, R.L., Monsell, S., & Wright, C.E. (1983). Control of rapid action sequences in speech and typing. Approximate text of a speech held at the Annual Meeting of the American Psychological Association.
Stornetta, W.S., Hogg, T., & Huberman, B.A. (1987). A dynamical approach to temporal pattern processing Proceedings of the IEEE conference on Neural Information Processing Systems, Denver.
Teulings, H.L., & Maarse, F.J. (1984). Digital recording and processing of handwriting movements. Human Movement Science, 3, 193-217.
Tam, D.C. & Perkel, D.H. (1989). A model for temporal correlation of biological neuronal spike trains. Proceedings of the IEEE International Joint Conference on Neural Networks 1989 Vol. I, 781-786.
Torras i Genís, C. (1986). Neural network model with rhythm-assimilation capacity. IEEE transactions on systems, man, and cybernetics, 16, 680-693.
Van Galen, G.P., Meulenbroek, R.G.J., & Hylkema, H. (1986). On the simultaneous processing of words, letters and strokes in handwriting: Evidence for a mixed linear and parallel model. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 5-20). Amsterdam: North-Holland.
Van Boxtel, A., & Schomaker, L.R.B. (1983). Motor unit firing rate during static contraction indicated by the surface EMG power spectrum. IEEE Transactions on Biomedical Engineering, 30, 601-609.
Van Galen, G.P., Smyth, M.M., & Meulenbroek, R.G.J. (1987). The role of visual feedback in the monitoring of the motor buffer in handwriting: An analysis of writing errors. (Abstract). Abstracts of the International Conference on Skilled Behaviour (p. 35). Brighton: Sussex University.
Von der Malsburg, C. (1988). Pattern Recognition by Labelled Graph Matching, Neural Networks 1(2), 141-148.
Watrous, R., & Shastri, L. (1987). Learning phonetic features using connectionist networks Proceedings of the 1987 IJCAI, Milano (pp. 851-854).
Williams, R.J., & Zipser, D. (1988). A learning algorithm for continually running fully recurrent neural networks. ICS Report 8805, La Jolla: UCSD, pp. 1-19.
Chapter 8
Inverse kinematics by neural networks
L.R.B. Schomaker
1 Introduction
Assuming that the problems of the representation of quantity and time are sufficiently dealt with in the preceding two chapters, it becomes interesting to ask how a motor system is able to control time functions of quantities (i.e., displacement or velocity), to produce handwriting movements with an effector system such as an arm. Both from human motor studies and in applied research in robotics it is becoming evident that for a motor control system, it is advantageous to perform the original movement planning in an internal representation of the extra-personal world instead of controlling the effectors by activation patterns based on a intra-personal representation of muscles and joints, solely. The ultimate goal of motor control is to exert a desired effect in the extra-personal space, thus it seems more appropriate to plan tasks like, e.g., collision avoidance, in a representation that is isomorphous to the workspace, than it is to perform this planning in the intra-personal representation of the effectors. In robotics, this insight is apparent from the control modes that are available for existing systems. Table 1 depicts the evolution of robotics, initially only allowing for control in an intra-corporal (intra-personal) representation in terms of joint angles. Gradually, the inclusion of the time and force domain develops as the field of robotics matures. The specification of kinematics is required to adapt to task demands (velocity) and minimize spatial error. The specification of kinetics (joint torques) allows for a further reduction in the spatial error, a reduction in the energy dissipation, a reduction of mechanical wear and the adaptation to task demands (e.g. torque values, given a required task-space contact force vector). The latter point also introduces the necessity for adaptive compliance control in object handling.
Table 1. Historical development of control modes in robotics.
|
It should be noted that there is a large discrepancy between industrial practice ("Phase 3") and academic interest ("Phase 6"). The development seems to indicate that an increasing number of variables must be controlled, going from effector-oriented control to task-oriented control. Does this imply that all these domains are under explicit and detailed pre-computed control in human motor control, where a very high degree of motor skills is present? It can be hypothesized that computational demands necessitate a different solution. Here, it is informative to take a look at the human motor system and a number of "natural" types of movement control. Table 2 gives an overview of different types of motor tasks and the domain on which the controlling system should focus to maximize the performance.
|
Table 2: Focus of control of a motor system and task type.
|
The notion of a "focus of control" does not imply that the subordinate domains are always completely neglected. In handwriting, for instance, compliance control can be autonomous (passive) if the writer configures the writing hand as a compressible mass-spring system, or the compliance is controlled according to a specific strategy as evidenced from pen force fluctuations (Schomaker, 1990). Thus, for each motor task, the essential control domain(s) can be determined. The problem, however, is the transformation of the task-domain constraints into intra-personal effector activation patterns. In most non-trivial motor tasks, this transformation concerns a limited number of degrees of freedom in task-space, and a large number of degrees of freedom in intra-personal space caused by an inherent redundance of the effector system. This type of problem is called ïll-posed" since there is no or no unique solution. In perception, there is a similar complementary problem in that one can never have enough optical sensors (eyes, cameras) to create an unambiguous internal representation of a natural visual scene. Given a number of limiting assumption beyond the scope of this thesis, and taking the kinematics domain as an example, one can write the transformation problem as:
| (11) |
where Q denotes the vector of joint angles in a manipulator, X and F denotes the end effector position and orientation with respect to the base, J is the Jacobian matrix. In words: small changes in joint angles Q can be calculated from the product of the inverse of the Jacobian, given the current manipulator state (Q), with the vector containing changes in X and F. So the Jacobian matrix must be non-singular, which is not generally true. In robotics, the geometry of manipulators is designed as to allow for a solution for the inverse of the Jacobian since the problem becomes rapidly intractable with an increasing number of degrees of freedom (joints). A well-known example is the standard 6-df industrial robot where the wrist is spherical (3 df), effectively only leaving 3-df for the actual position control. Given the geometrical and mechanical complexity of the human motor system, the analytical approach is of little use. The ease with which we perform complex motor tasks exemplifies that the biological motor system apparently found a solution to this problem. The question arises what type of neural architecture is involved in this essential aspect of motor control. If we look at human movements, the following aspects are apparent:
- The number of anatomical degrees of freedom
is very large.
- Movement and reaction times do not depend on the number of
degrees of freedom involved in a motor action.
- Stiffness regulation and the amount of activity per joint
can be controlled dynamically, as opposed to the equalized solution that
existing algorithms for the calculation of inverse kinematics provide.
- Movement time of fast, ballistic movements depends on the
required accuracy by MT=a + b log2 (2A/W) (Fitts' law) where MT
is movement time, A is amplitude of movement, and W is diameter
of target.
- Human movements are less accurate than are those of a mechanical manipulator.
An ideal model of motor control should account for these observations. For example, if in humans the calculation of inverse kinematics were be done by active computation according to an analytical model (Luh & Lin, 1984), even one would expect a strong relation between movement complexity and reaction time. This is not the case. Pressing a button or starting to run in a steeple-chase occur with approximately equal reaction times. Looking at the inverse kinematics transformation problem, it appears that there are two functions involved: the transformation problem as such, e.g. from Cartesian or low-dimensional space to angular high-dimensional space, and the handling of redundance, sec. Later in this chapter, two small-scale experiments will be reported on neural network solutions to the transformation problem as such. Alternatives to the closed form (with a Jacobian) are the "table lookup" (Albus, 1975), feedforward neural networks (Josin, 1988; Kuperstein & Rubinstein, 1989; Massone & Bizzi, 1990; Pellionisz & Llinas, 1980), Hopfield networks (Gielen & Coolen, 1989), and dedicated neural network models (Eckmiller, 1988).
A general, unified model of motor control has evolved gradually from work by Bizzi (1980), Hogan (1985), Morasso & Tagliasco (1986), Morasso & Mussa Ivaldi (1987), and others. As a starting point, this model considers muscles to be tunable springs. The next step is to assume a potential elastic energy field (PEF), generated by the manipulator system as a whole. The shape of the energy landscape is determined by the spring-like characteristics of a large number of individual muscles and their mechanical connectivity with respect to the anatomy of the limb segments (bones and ligaments). According to this theory, motor control is not so much the specification of local muscle activity to obtain a local joint angle or torque, but rather a shaping of the elastic energy field. The system will tend to maintain a configuration of minimum potential energy. Changing the shape of the energy landscape yields movements along a virtual trajectory. If the manipulator meets an external object, the resulting size and direction of force depends on the energy difference between the current imposed state and the target state. Such a model reduces the redundance problem to a large extent. However, more constraints are needed (see Table 2) in many motor tasks. Also, the motor control system must occasionally make decisions, e.g., to choose from several end-effector approaching strategies (Rosenbaum et al., 1990), to solve the redundance. Nevertheless, the PEF model is very attractive as a starting point. For instance, stiffness control can be represented as deepening sinks in the PEF field, which can be achieved by increased muscular co-contraction. New findings indicate that stiffness control may be related to movement duration as specified in Fitts' Law (Van Galen & Schomaker, 1991). High stiffness ensures higher stability in case of the small ("difficult") target sizes of a Fitts experiment. Increased co-contraction means increased stiffness, reducing the gain of the mechanical transfer function of the effector system. The motor control system has the choice to either elongate movement duration or to put in more force. The latter strategy, however, yields higher instability, which is inconsistent with the motor task demands. Consequently, movement duration is scaled. However, more experimental work is needed to confirm this stiffness-related explanation of Fitts' Law.
2 Two modeling experiments with a planar arm
The PEF model, or ëquilibrium theory" still requires a transformation from target space to intra-personal effector space. The learning of the inverse kinematics transformation on the basis of random limb segment movements ("motor babbling") was tested on two network types:
- A Kohonen-type net, learning feature vector quantization (LVQ)
- A 3-layer perceptron, trained by back-propagation (MLP)
A planar arm, 3 df, with constrained joint angle ranges was used. Teaching was done by generating random joint angles qi and presenting end effector position and joint angles to the Kohonen network. The multi-layer perceptron also received specification of the end effector orientation (Phi), as it was evident in an early stage that learning was difficult on the basis of position alone. Arm parameters (limb segment proportions approximating a human arm) are as follows:
| Joint | Limb | qmin | qmax |
| 1 | 0.500 | 30.0 | 250.0 |
| 2 | 0.375 | 30.0 | 170.0 |
| 3 | 0.100 | 140.0 | 190.0 |
From pilot studies it was evident that these constraints are essential in reducing the solution space and in minimizing the occurrence of singularities. It can be hypothesized that hard constraints like the maximum of 180 degrees for a human elbow angle not only introduce mechanical stability, but also alleviate the problem of learning a body representation.

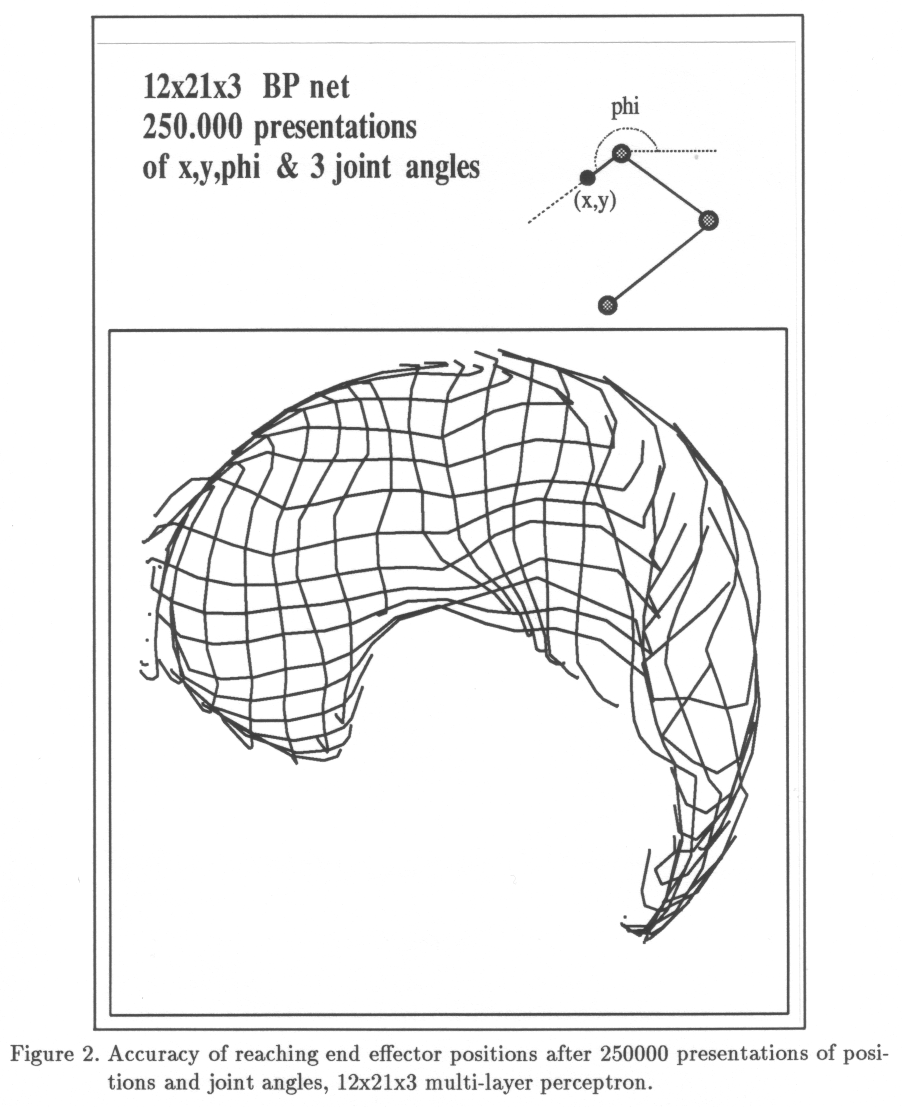
Figures 1 and 2 show a grid of obtained end effector positions, testing the total work field, x=[-40,40]. y=[-40,40]. Both figures show the general shape of the work field for such an arm. Clearly the Kohonen LVQ net outperformed the multi-layer perceptron (MLP), but it also has a much larger number of cells than the MLP (1600 vs 36), and is more or less a table-lookup solution.
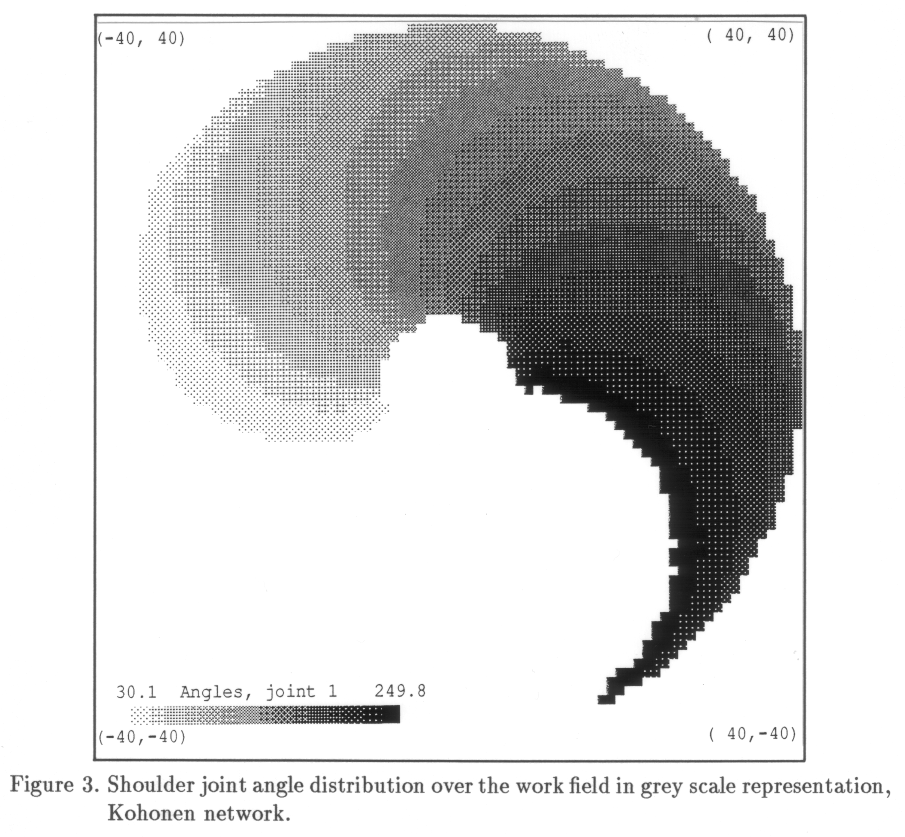

Figures 3 and 4 show the joint angle nomogram over the work field, for the shoulder joint (=1) (Figure 3) and the elbow joint (=2) (Figure 4). Apart from the typical work field shape, it is evident that joint angles vary smoothly.
Summary of results:
Kohonen LVQ:
- Learning is faster than in the MLP
- An äverage solution" is found
- Spatial error is distributed almost homogeneously over the work field
- Many units (columns) are needed: Nx Ny (Njoint+Npos.)
- The öut-of-bounds" behavior is predictable
A Multi-layer perceptron (MLP) trained by back propagation:
- Learning is slow
- A limited number of cells is needed, compared to the LVQ network
- A stable average solution was not found after 80000 presentations
- The öut-of-bounds" behavior is unpredictable
Unpredictable öut-of-bounds" behavior refers to the situation where the planning agent specifies an end effector location outside the work field. In this case, evidently, ego-motion is implicitly required. An MLP just produces unpredictable values for the joint angles, whereas in the LVQ network, the mechanism of thresholding can be used to detect öut-of-bounds" coordinates, since vectors that did not occur during training contain unspecified values. The disadvantage of the LVQ network in terms of the number of units that are needed to represent the effector system becomes clear if one realizes that apart from the joint angles, also joint torques need to be specified. In object manipulation, the parameterization of other solutions than the average arm configuration necessitates an even higher-dimensional representation of the effector, making a topological implementation unlikely, unless modulation of the LVQ feature space itself can be described and explained. In MLP networks, on the other hand, parametrization can be obtained relatively easy by adding input lines, theoretically. In practice, however, as becomes evident from the current experiments, training complete-workfield inverse kinematics for a redundant arm to an MLP by standard back propagation appears to be difficult. More research is needed to find out how we can reconcile the notions of topological body representation and distributed multi-layer neural pattern transformations.
3 Conclusion
In the modeling experiments, we considered the representation of a 2-D workspace of a 3-df arm. In experimenting with these models, it became clear that the regular use of the term Degree of Freedom is confusing. Since joint angles in biological arms have a limited range, it would be better to speak of Degrees of Limited Freedom. A self-organizing system with unconstrained joint angles will experience more difficulty representing a mapping from task space to effector space than a system with constrained joints. More specifically, the fact that the human elbow has a working range of 20 to 180 degrees instead of, say, 340 degrees is very likely to enhance self-organized learning of the effector system in "motor babbling" to a significant extent.For demonstration purposes, the LVQ network was succesfully used to simulate large handwriting movements like a human would produce on a school blackboard by upper arm, forearm and wrist movements, holding the fingers in a fixed attitude. As such, this is not more than an illustration that the inverse kinematics transform using this method works in practice.
Summarizing, the redundance problem in motor control can be largely reduced, by assuming (a) a potential elastic energy field model (equilibrium theory), (b) by considering internal effector constraints like working range of joint angles and torques, and, last but not least, (c) the motor task requirements. From the neural network modeling point of view, the challenge is to translate these insights into a working model of human motor control.
4 References
Albus, J.S. (1975). A new approach to manipulator control: the cerebellar model articulated controller (CMAC). Journal of dynamic systems, measurement, controls, 94, 220-227.
Bizzi, E. (1980). Central and peripheral mechanisms in motor control. In G.E. Stelmach & J. Requin (Eds.), Advances in psychology 1: Tutorials in motor behavior (pp. 131-143). Amsterdam: North Holland.
Brady, M., Hollerbach, J.M., Johnson, T.L., Lozano-Pérez, T., & Mason, M.T. (1982). Robot Motion: Planning and Control. Cambridge: MIT.
Desa, S., & Roth, B. (1985). Mechanics: Kinematics and dynamics. In G. Beni & S. Hackwood (Eds.) Recent advances in robotics (pp. 71-130). New York: Wiley.
Eckmiller, R. (1988). Concept of a 4-joint machine with neural net control for the generation of 2-dimensional trajectories. Abstracts of the 1st annual INNS meeting, Boston, 1988, Neural Networks (journal of the INNS) (p. 334). New York: Pergamon.
Gielen, C.C.A.M., & Coolen, A.C.C. (1989). Self-organization in neural networks underlying the coordination of movements. In J. Schopman (Ed.), Publications Series. Vol 24. Utrecht: The department of epistomology and philosophy, Utrecht University (The Netherlands)
Hogan, N. (1985). The mechanics of multi-joint posture and movement control. Biological Cybernetics, 52, 315-331.
Josin, G. (1988). Neural-Space generalization of a topological transformation Biological Cybernetics, 59, 283-190.
Kohonen, T. (1987). Adaptive, associative, and self-organizing functions in neural computing. Applied Optics, 26, 4910-4917.
Kuperstein, M. & Rubinstein, J. (1989). Implementation of an adaptive neural controller for sensory-motor coordination. In: R. Pfeifer, Z., Schreter, F. Fogelman-Soulie, & L. Steels, Connectionism in Perspective (49-61). Amsterdam: Elsevier.
Luh, J.Y.S., & Lin, C.S. (1984). Approximate joint trajectories for control of industrial robots along cartesian paths. IEEE Transactions on Systems, Man, and Cybernetics, 14, 444-450.
Massone, L. & Bizzi, E. (1990). On the role of input representations in sensorimotor mapping. Proceedings of the IEEE International Joint Conference on Neural Networks 1990 Vol. I, 173-176.
Morasso, P. & Tagliasco, V. (1986). Human Movement Understanding. Amsterdam: North-Holland.
Morasso, P., & Mussa Ivaldi, F.A. (1987). Computational models of handwriting. In R. Plamondon, C.Y. Suen, J.-G. Deschênes, & G. Poulin (Eds.), Proceedings of the Third International Symposium on Handwriting and Computer Applications (pp. 8-9). Montreal: Ecole Polytechnique.
Pellionisz, A. & Llinas, R. (1980). Tensorial approach to the geometry of the brain function: Cerebellar coordination via a metric tensor, Neuroscience, 5, 1125-1136.
Rosenbaum, D.A., Vaughan, J., Barnes, H.J., Marchak, F. & Slotta, J. (1990). Constraints on action selection: Overhand versus underhand grips. In M. Jeannerod (Ed.), Attention and Performance XIII (pp. 321-342). Hillsdale, NJ: Lawrence Erlbaum.
Schomaker, L.R.B. (1990). The Relation between Pen Force and Pen Point Kinematics in Handwriting. Biological Cybernetics, 63, 277-289.
Van Galen, G.P. & Schomaker, L.R.B. (1991, in press). Fitts' Law as a Low-Pass Filter Effect of Muscle Stifness. Human Movement Science, x, pp. xxx-xxx.
Chapter 9
Recognition of cursive handwriting movements
The complementary approach to the simulated production of handwriting movements by a computer is the automatic recognition of original handwriting movements that are being produced by the human writer. Schematically:
| Simulation: | Discrete Symbols | ® | Continuous Movement |
| Recognition: | Continuous Movement | ® | Discrete Symbols |
In the simulation process, inherently
discrete entities had to be connected in
a fluent way. In the handwriting movement recognition process, an inherently
continuous stream of actions must be segmented in
discrete entities,
representing a sequence of characters.
This chapter describes how knowledge of
the motor system in handwriting can be used in an on-line handwriting
recognition system. Also, the knowledge that has been collected about the
properties and peculiarities of the handwriting movement signals as recorded by
a digitizer in the analysis of experimental data will be used in the
implementation of a recognition system. Methods have been developed to estimate
typical parameters of handwriting, e.g. estimating baseline orientation,
recovering the lineation from the displacement signal, detecting loops, and
describing individual stroke shapes. Automatic handwriting description and
recognition methods can also be used in the analysis of experimental data.
As an example, the description of a writer's Cursive Connections
Grammar
(Chapter 3) has been a manual, interactive procedure. The further development
of recognition techniques will allow for a solution to this problem, minimizing
manual intervention.
A Handwriting Recognition System Based on Properties of the Human Motor System 13
Lambert R.B. Schomaker &
H.L. Teulings
Abstract
The human reader of handwriting is unaware of the amount of background knowledge that is constantly being used by a massive parallel computer, his brain, to decipher cursive script. Artificial cursive script recognizers do not have access to a comparable source of knowledge or of comparable computational power to perform top-down processing. Therefore, in an artificial script recognizer, there is a strong demand for reliable bottom-up processing. For the recognition of unrestricted script consisting of arbitrary character sequences, on-line recorded handwriting signals offer a more solid basis than the optically obtained grey-scale image of a written pen trace, because of the temporal information and the inherent vectorial description of shape. The enhanced bottom-up processing is based on implementing knowledge of the motor system in the handwriting recognition system. The bottom-up information will already be sufficient to recognize clearly written and unambiguous input. However, ambiguous shape sequences, such as vs or vs , and sloppy stroke patterns still require top-down processing. The present paper discusses the handwriting recognition system as being developed at the NICI. The system contains six major modules: (1) On-line digitizing, pre-processing of the movements and segmentation into strokes. (2) Normalization of global handwriting parameters. (3) Extraction of motorically invariant, real-valued, feature values per stroke to form a multi-dimensional feature vector and subsequent feature vector quantization by a self-organizing two-dimensional Kohonen network. (4) Allograph construction, using a second network of transition probabilities between cell activation patterns of the Kohonen network. (5) Optional word hypothesization. (6) The system has to be trained by supervised learning, the user indicating prototypical stroke sequences and their symbolic interpretation (letter or N-gram naming).
1 Introduction
There are many advantages if data can be entered into a computer via handwriting rather than via typing (Teulings, Schomaker & Maarse, 1988). These advantages are acknowledged by hardware manufacturers who are testing the market with 'electronic paper' with built-in computer systems for recognizing elementary pen movements (e.g., Hayes, 1989). Electronic paper consists of an integrated liquid crystal display (LCD) plus digitizer. Although the user acceptance of this kind of hardware will depend on the solution of some technical and ergonomical problems that are currently present (visual parallax, surface texture, stylus wire), it seems relevant to develop on-line handwriting recognition systems for unconstrained handwriting. Several commercial systems exist that recognize on-line handprint, but cursive script recognition has still not been solved satisfactorily (Tappert et al., 1988). Ideally, a recognition system should be able to recognize both handprint, for accuracy, and cursive script, for optimal writing speed. However, the major problem in cursive-script recognition is the segmentation of a word into its constituting allographs prior to recognizing them, while the allographs have different numbers of strokes (Maier, 1986). Indeed, even for human readers cursive script is sometimes ambiguous. One advantage of on-line recognition is that in case the system is not able to disambiguate, the correct output can be provided by the user interactively. However, the most important advantage of including on-line movement information is, that it contains more information than the unthinned, quantized images of the optically digitized pen traces. Consider for instance the final allograph which may appear in the spatial domain as a single horizontal curl, but in the time domain still displays the three pen-speed minima. This kind of extra information is needed to compensate for the large amount of top-down processing done by the 'understanding' human reader of handwriting. The enhanced bottom-up processing is based on implementing knowledge of the motor system in the handwriting recognition system. Our efforts to introduce handwriting as an acceptable skill in the office environment has resulted in a multinational consortium (PAPYRUS) aimed at building software and hardware for a simple electronic note book, allowing the user to enter data into a computer without using a keyboard.
In Teulings et al. (1987) a modular architecture for the low-level bottom-up analysis of handwriting was introduced, our so-called Virtual Handwriting System (VHS). The present paper discusses the handwriting recognition system as being developed at the NICI. The system contains six major modules which are also found in several other recognition systems (e.g., Srihari & Bozinovic, 1987, for off-line handwriting).
- On-line recording of handwriting, pre-processing consisting of lowpass filtering and differentiation and finally, segmentation into intended movement units ('strokes').
- Normalization of various motorical degrees of freedom.
- Computation of feature values ('feature vector') per stroke which are motor invariants or salient to the human perceptual system, followed by the quantization of stroke shapes using a self-organizing Kohonen network.
- Construction of letter (allographic) hypotheses from sequences of quantized strokes.
- Construction of word hypotheses from sequences of allographic hypotheses.
- Supervised learning of the relation between stroke-vector sequences and allographs.
Below, these modules will be discussed in terms of their purpose, the knowledge of the motor system or the perceptual system used, its realization and its performance.
2 Recording, Pre-processing, and Segmentation
The pre-processing stage consists of all operations needed to provide a solid base for further processing. At this stage the data consist of a continuous signal without any structure. The first operation is to split the continuous signal into batches that can be processed separately. We suggest that a word is the easiest batch to be processed. Then for each word, the signal, containing noise from different sources (e.g., the digitizing device), is low-pass filtered. Finally the continuous movement is segmented into basic movement units. Knowledge of the human motor system provides an empirically and theoretically basis for the segmentation heuristics.
The control of the muscles involved in producing the writing movements is of a ballistic nature: each stroke has only a single velocity maximum (Maarse et al., 1987) and a typical duration between 90 and 150 ms. Shorter-lasting motorical actions are very unlikely to be the result of intentional muscle contractions. For an appropriate pre-processing it is relevant to understand the frequency spectrum of handwriting movements. The displacement spectrum contains a large portion of very low-frequency activity, mainly due to the ramp-like shape of the horizontal displacement. This is not true for pen movement direction and velocity. The latter signal is estimated by calculating the first time derivative. The differentiation suppresses the low-frequency components that are present in the displacement spectrum, and a more informative spectral shape emerges. In Teulings & Maarse (1984) it has been shown that the velocity amplitude spectrum is virtually flat from 1 to 5 Hz where it has a small peak and then declines to approach the noise level at about 10 Hz. Therefore, a low-pass filter with a flat pass band from zero to 10 Hz will remove the high-frequency noise portion of the signal while leaving the relevant spectral components of the handwriting movement unaltered. In order to prevent oscillations (Gibbs phenomenon) it has been shown that the transition band should not be too narrow (e.g., at least 8/3 of the width of the passband). From the bandwidth of at least 5 Hz follows that the movement can be most parsimoniously represented by about 10 samples per second. Since the endpoints of the strokes appear to be about 100 ms apart, the time and position of the stroke endpoints as determined by two consecutive minima in the absolute velocity are a good basis for reconstruction (Plamondon & Maarse, 1989). Points of minimum velocity correspond with peaks in the curvature (Thomassen & Teulings, 1985).
Realizing that the vertical movements appear to be less irregular than the horizontal progression, Teulings et al., (1987) suggested to weigh the vertical component higher than the horizontal component in the calculation of a biased absolute velocity signal (up to factor of 10).
Handwriting movements are recorded on a CalComp2500 digitizer with a resolution of about 0.1 mm and a sampling frequency of 125 Hz using a pen which contains a solid state transducer to measure the axial pen pressure synchronously with pen tip position. A pressure threshold serves as a sensitive pen on/off paper detector. The data were not corrected for non-simultaneous sampling of x and y (Teulings & Maarse, 1984) nor for variations of pen tilt (Maarse, Janssen & Dexel, 1988).
Filtering, and time derivation are done using frequency domain fast Fourier transforms. In stroke segmentation, time points are chosen which are about 100 ms or more apart. This is done by selecting the lowest absolute velocity minimum within a time window of 50 ms around a given minimum (Teulings & Maarse, 1984).
Word segmentation is not based on particular information of the motor system but rather on perceptual cues. It is done by detecting a fixed horizontal displacement while the pen is travelling above the paper beyond the right or the left boundary of the last pen-down trajectory.
The performance of this straight-forward pre-processing does not appear to be the main source of recognition error in the present system.
3 Normalization
A particular problem in handwriting recognition is its extensive variability. A given letter can be produced in several ways, each having its own typical shape, e.g., lower case vs upper case or the well-known different variants of the . The shape variants for a given letter are called allographs. Thus, first there is the between-allograph variability (I): a writer might select different letter shapes in different conditions or at free will. Second, there is the within-allograph shape variation in which the topology of the pattern is not distorted (II), the error source being (psycho)motor variability. Topology can be defined as the number of strokes and their coarsely quantized relative endpoint positions. Third, there is the within-allograph shape variation which actually does distort the topology of the pattern, by the fusion of two consecutive strokes into a single ballistic movement (III) in fast and/or sloppy writing. These three types of variabilities will all be prevalent to some degree under different conditions. Table 1. gives an impression of the estimated order of these variabilities depending on context and writer. The context of a given allograph is defined as the identity of the allographic neighbors and the serial position of the target allograph.
Table 1. The estimated order of
the degree of handwriting
variability
that a script recognition system has to handle, under
different conditions, for all three types (I-III) of variability (1= minimum
variability, 4=maximum variability).
| Context | ||
| Writer | Identical | Different |
| Identical | 1 | 2 |
| Different | 3 | 4 |
In order to extract the sequence of feature vectors of the handwriting input, several normalization steps can be performed (See Thomassen et al., 1988, for an overview). The reason is that a sample of a person's handwriting contains various global subject-specific parameters, like slant or width of the allographs (e.g., Maarse, Schomaker & Teulings, 1988). Also, the motor system is able to transform handwriting deliberately, e.g., changing orientation, size or slant (e.g., Pick & Teulings, 1983). However, these global parameters do not contain any information about the identity of the characters. Therefore, the handwriting patterns have to be normalized in terms of orientation, vertical size, and slant (Thomassen et al., 1988).
It may be anticipated that several alternative normalization procedures can be proposed. We require the system to try them all and to learn to use the most appropriate ones. As such it resembles Crossman's (1959) statistical motor-learning model: a person has a repertoire of several methods for every action and learns with time which of those is most appropriate.
Orientation is defined as the direction of the imaginary base line. Vertical size consists of three components: body height, ascender height and descender height relative to the base line. Slant is defined as the general direction of the vertical down strokes in handwriting (e.g., Maarse & Thomassen, 1983). The normalization consists of estimating these parameters and then performing a normalization by a linear planar transformation towards horizontal orientation and upright.
Various algorithms to estimate the parameters for each normalization step are available and not every algorithm may be appropriate in all conditions. Averaging these estimates is probably not the best choice because one estimator ('demon') may be totally wrong. A sub-optimal choice of the orientation, for instance, has dramatic effects in the subsequent normalization of size or slant. The solution we propose is to have the system select the best available, unused estimator using the estimators' current confidence and the proven correctness in the past using a Bayesian approach (Teulings et al., 1990). This prevents an exponential increase in computational demands with an increasing number of estimator algorithms (demons).
The normalization estimators have not yet been evaluated statistically. However, both in artificial data (using bimodally distributed estimates of different variance) and in handwriting data (using a prototype system with parallel processes), the system produces stable and optimized estimates within 30 trials. We observe that the system backtracks immediately to the normalization level where apparently an inappropriate estimator was chosen first, after which the second best alternative is evaluated. Even though calculation is reduced by taking the 'best first' approach, a multiple estimator scheme requires a lot of computation. However, due to the modularity of the approach, a solution by means of a network of transputers is very well possible. As we are still in a stage of testing with only two writers this system was not used currently. Only vertical-size normalization was performed using one estimator. The effects of vertical size normalization are relatively small as it is only one of several features. Orientation was standardized by lined paper on the digitizer and slant can be assumed approximately constant within a writer in a standard condition (Maarse, Schomaker & Teulings, 1988). However, slant does seem to be influenced by the orientation of the digitizer if it is located more distally than normal, e.g., to the right of the keyboard in a typical workstation setting instead of directly in front of the writer. It was observed that the feature quantization network partially counteracted these slant variations as evidenced by reconstruction of the handwriting trace.
4 Feature extraction
Each stroke of the normalized handwriting pattern must be quantified in terms of a set of features, a feature vector, that describes the raw coordinates in a more parsimonious way. It is important to use features that show a relative invariance across replications and across different contexts. As a check for the completeness of the feature set the original pattern must be reconstructable from these features. Finally, in order to facilitate the subsequent classification and recognition stages the feature vector itself should be quantized into a lower-dimensional representation space.
We employ a set of features which is related to the underlying hypothetical motor commands and which is complemented by a few visual features. The feature vector comprises 14 features. Only nine of them are related to the stroke itself whereas five refer to the previous or the following stroke and are included to capture between-stroke context effects. The procedure to select appropriate features is to write a number of identical patterns (e.g., 16) at two speed conditions (normal and at higher speed, respectively). The invariance of a feature of a particular stroke in those patterns can be tested by estimating its Signal-to-Noise Ratio (SNR) (Teulings et al., 1986). The advantage is that SNRs of totally different features can be compared and the ones with the highest SNR can be selected. The preliminary data presented here are based on the central 28 strokes of the word 'elementary' produced by one subject. It appears that the SNRs are remarkably constant between the two speed conditions such that only the averages are presented. In order to assess the invariance across conditions, the between-condition correlation of the average stroke patterns of a feature is employed.
The features currently employed are:
(a) The vertical positions of the beginning (Yb) and end of a stroke (Ye) relative to the base line and the path length of the stroke (S) all scaled to the average body height, also called x-height, referring to the lower case x. In Teulings et al. (1986) it has been indicated that especially the relative (vertical) stroke sizes are invariant. The SNRs of Ye or Yb are 4.9, and the SNR of S is 4.7, which are typical values for spatial characteristics. The between-condition correlations are as high as 0.99.
(b) The directions fn of the five, straight stroke segments between two subsequent points corresponding with the time moments
|
(c) The size of the enclosed area between the end of the stroke and the subsequent stroke (le) is rather a visually salient feature. The SNR of le is 5.6 and the between-condition correlation is as high as 0.999.
(d) A pen up indicator (P), which shows whether the pen is predominantly up or down during a stroke. It may be noted that strokes above the paper also count as strokes. As this is a rather coarse binary signal we refrained from presenting any statistics.
In summary, the selected features show absolutely high SNRs and high between-condition correlations which indicates that these features contain the basic information, which constrains the actual movement. As such, these features are attractive to use in a recognition system. Whether this set of features is also a complete one, can only be demonstrated empirically.
It is trivial to estimate the feature values per stroke. It is, however, less trivial to quantify the distance between feature vectors. An elegant method to solve the problem of irregularly shaped probability distribution functions of the feature vector of classes is vector quantization by an artificial self-organizing neural network (Kohonen, 1984; Morasso, 1989; Morasso et al., 1990). This type of network performs, in a non-supervised way, a tesselation of cell units into regions, each corresponding to a particular prototypical feature vector. The statistical properties of the training set of feature vectors will determine the emergence of the prototypical feature vector set. We have used a 20x20 network. Bubble radius and learning constant a decrease linearly with the number of iterations, from 20 to 1 and from 0.8 to 0.2, respectively. The shape of the connectivity within a bubble was a monopolar and positive rectangular boxcar. The total set of strokes was presented 100 times to the network. Cells representing a quantized vector were arranged in a hexagonal grid.
The completeness of the reduced data is tested by two reconstruction methods. In the first method, the writing trace is reconstructed from the sequence of feature vectors. An average Euclidean distance measure between reconstructed and original pattern is used to express the accuracy of reconstruction, and thus, the quality of the segmentation procedure as well as the information value of the selected features. In the second method, each feature vector is presented to the Kohonen network, and will be substituted by the nearest prototypical feature vector. The sequence of strokes thus yields a sequence of prototypical feature vectors that can be used to reconstruct the original trace in a similar way as described above. The accuracy of this reconstruction yields a second distance measure. It indicates the quality of the feature vector quantization imposed by the Kohonen network.
The patterns produced by both reconstruction methods are legible, which is in fact the crucial criterion rather than a spatial goodness of fit. Furthermore, the reconstructed patterns lack individual and context-dependent characteristics which stresses that the selected features reduce the writer dependence as well. For example, slant variations due to imperfect normalization will be counteracted by the Kohonen network as single strokes are attracted to their closest, general prototypes.
5 Allograph hypothesization
At this stage the writing pattern is represented as a sequence of prototypical strokes. In earlier experiments, we have used a Viterbi algorithm using a lexicon of allographs. Each prototypical allograph was represented by its average feature vector (no feature vector quantization was performed). A Euclidian distance measure was used that was adapted to angular measures (Teulings et al, 1990). The problem with this approach was, that for a given stroke position, there is a distance measure with each of the M=26 prototypes. Solution space is a matrix of MxN, where N is the number of stroke positions. Since the allographs mostly have an unequal number of strokes, the plain Viterbi algorithm could not be used. Instead an iterative version was developed, trying to recognize 1-stroke solutions, 2-stroke-solutions, and so on, until the N-stroke solution. The path cost factor was the modified Euclidean distance, optionally combined with a digram transition probability, each term having its own weight. The results of this technique were rather poor so we decided to find a method that yields a smaller solution space, on the basis of quantized feature vectors. Another approach used was to use 6 feedforward perceptrons, (Nx400)x160x26, trained by back propagation, one perceptron for each class of N-stroked allographs, N=1,...,6. This approach, too, yielded too many hypotheses in the MxN matrix. This problem can possibly be alleviated to some extent by introducing competition among the output layers of different perceptrons. Another solution is proposed by Skrzypek & Hoffman (1989), who introduce a final judgment perceptron to combine the output of the N lower layers. The problem is, however, that for the recognition of varying-length temporal patterns, an optimal neural architecture does not exist, yet. Of the known architectures, recurrent nets (Jordan, 1985) are hampered by their limited ability to handle long sequences. Temporal flow nets (Stornetta et al., 1987; Watrous & Shastri, 1987) are currently being tested in speech recognition.
In Teulings et al. (1983) it was indicated that complete allographs are probably stored at the level of long-term motor memory. An interesting question is to what extent the strokes belonging to one allograph have to be kept together and whether the strokes of different realizations of the same allograph may be assembled to yield a new allograph. The directions of the stroke segments introduced before (i.e., fb4, fb5, f1, ...) show that the correlations between subsequent stroke segments within one stroke range between 0.69 and 0.90 (mean 0.80) whereas the correlations between subsequent stroke segments across the separation of two strokes range between 0.47 and 0.53 (mean 0.50). This implies that even in identical contexts, subsequent strokes are relatively independent. This suggests indeed that allographs are probably built up of different strokes that may be assembled from other similar allographs.
Rather than performing a template matching between prototypical allographs and an input sequence of strokes, the method we developed at this stage is based on the idea of an active construction of allograph hypotheses. This is done by a neurally inspired algorithm. Once the writer has labeled allographs interactively, and thus created a data base covering a wide range of allographs in different contexts, the system collects, for each prototypical stroke, its possible interpretations. The representation is based on the reasonable assumption that the fundamental (root) feature of an allograph is its number of strokes. Thus, two allographs are definitely different if their number of strokes differs. Each stroke interpretation has the general form Name(Istroke/Nstroke). Thus, a given stroke may be interpreted as representing one element of the set { a(1/3),d(1/3),o(1/2),c(1/1)}. The construction of an allograph is a left-to-right process, where the activation level of an allograph hypothesis increases stepwise with each interpretation that is a continuation of a previously started trace. The advantage over storing prototypical allographs is evident: after labeling three, 3-stroked sequences, each representing the allograph , the network will recognize an that corresponds to any one of the 27 combinations. The method does not exclude the use of digrams or trigrams as graphical entities. However, the computational load on a sequential computer will increase quadratically with an increasing number of interpretations per prototypical stroke, so the use of trigrams is impractical.
Table 2 presents the recognition results of two types of handwriting. In Section 6. the training procedures have been reported for each of the two writers. It may be stated that these results have been achieved on unrestricted cursive script of lower case letters without the use of linguistic post processing by means of a lexicon. On the other hand, the data are optimistic as in case of alternative allograph hypotheses (on average about 2 alternatives) the appropriate one was accepted. This was done under the assumption that only linguistic post-processing will be able to solve these true ambiguities. For instance, and are sometimes written identically.
Table 2. The recognition rates of allographs and of allograph strokes of five different text samples from two writers.
| Subj. | Text | Words | Time | Allo- | Recog- | Strokes | Strokes in | R ecog- | ||
| graphs | nized | allographs | nized | |||||||
| # | (s) | # | # | % | # | # | # | % | ||
| A | AP87 | 40 | 281 | 236 | 153 | 65 | 668 | 525 | 368 | 70 |
| A | FE90 | 51 | 224 | 275 | 243 | 88 | 862 | 702 | 657 | 94 |
| A | TEKST | 51 | 89 | 262 | 198 | 76 | 755 | 633 | 542 | 86 |
| B | TEST1 | 54 | 221 | 299 | 209 | 70 | 987 | 786 | 544 | 69 |
| B | TEST2 | 60 | 234 | 300 | 229 | 76 | 965 | 813 | 608 | 75 |
Note the difference between the number of strokes that is actually part of
an allograph and the total number of strokes. Apparently 18.4% of all
strokes cannot be attributed to letters because they are
connecting strokes,
hesitation fragments, or editing movements. Note that there has been no
post processing in any sense. Figure 1 gives an impression of the
processing stages and the solution space for the word .
In the reconstructed patterns, circles indicate detection of
a loop (le ¹ 0).
Going from bottom to top, the solution space (d) is liberally filled with
hypotheses of decreasing length as expressed in number of strokes. Shorter
hypotheses may 'fall down' in holes that are not filled by hypotheses of
greater length. Each '-' indicates an allograph stroke, a '*' indicates
a stroke that is not part of an allograph in the target word.

6 Optional word hypothesization
Apart from yielding a list of hypothesized allographs the bottom-up information contains also information to narrow down the number of possibly written words in a word lexicon. The word in the list with the minimum distance from a word in the lexicon can be selected. However, if the bottom-up process is rather certain of a given hypothesized word, then it seems superfluous to use additional lexical top-down processing.
It is known that when writing redundant character sequences (i.e., words or parts of words that could be recovered with a lexicon of words) the writer uses less efforts to produce the allographs neatly.
From human reading research we know that ascenders and descenders (i.e., the contour) are strong cues to recognize the presented word, similar to the function of consonants in speech recognition.
For the coding of the ascender and descender contour of a word the following coding scheme is proposed. Contours are assumed to be equal if their pattern of ascenders, descenders, and body-sized objects correspond. The body-size characters are recoded as "o", the descender stroke of is recoded as "j", the ascender stroke of is recoded as "l", whereas the is a unique class "f" because it spans both the ascender and descender area in cursive script. In this coding, a is a combination of an ascender object and a body-sized object, i.e., "lo". This coding assumes that the letters as such have been identified. However, if a repetition of N body-size characters N"o" is coded by "x", a compressed coding is formed which is not based on the number of letters in a word. For instance, the word 'they' can be coded by "lloooj" in letter-dependent code, and by "llxj" in compressed code. For the time being no special attention is paid to the allographs with dots .
Although the word-hypothesization stage has not yet been integrated it is of interest to mention its potential performance. Letter-dependent contour coding of a Dutch lexicon of 48000 common words yielded a collision of 4 word hypotheses on average for a given code pattern, with a worst case of 398 collisions for the code "oooooo". A number of 84.5% of the codes has a number of collisions less or equal to the average of 4. Modal code pattern length was 9 codes.
Compressed contour coding yielded an average collision of 24 word hypotheses, with a worst case of 1953 collisions for the code "xlx". In this case, a number of 89.3% of the codes has a number of collisions less or equal to the average of 24. Modal code pattern length was 5 codes.
The consequences of these figures for recognition are the following. First, letter-dependent coding is practically of no use since it is the letter identification itself which is the objective in cursive script recognition. Thus, only compressed contour coding is useful. The actual gain depends on the linguistic frequencies of the words in the different code groups. These frequencies are currently being analyzed.
7 Supervised learning
Before a cursive-script recognition system is ready to work, it has to learn how to segment a writing pattern in the to-be-recognized allographs. The segmentation into allographs of handprint, with sufficient distance between individual allographs (e.g., spaced discrete characters, Tappert, 1986), would be relatively straightforward. If the written text is available, the learning module could just assign each allograph within the context of a word to a character. Although it is a rather cumbersome task to teach a system each allograph that may occur in a person's handwriting, it is currently still the most reliable procedure. The reason is that the allograph boundaries in cursive script have to be specified somehow.
Several methods for performing this task in a non-supervised fashion are being developed (Morasso et al., 1990; Teulings et al., 1990). Maier (1986) tried to segment an unknown writing trace into allographs using a-priori assumptions about the shape of the connecting strokes between allographs. However, such a method produces persistent errors (e.g., segmenting allographs like cursive , or into two parts). Therefore, teaching is presently done interactively by the user.
Although this stage is rather artificial it is still important to make the job as ergonomic as possible. During supervised learning the experimenter has to tell the system which parts of the handwriting trace belong to which allograph. It is relatively easy for the perceptual system if the user has to point only to complete strokes belong to a certain allograph. The initial connecting stroke of the cursive allographs and is not included and the initial connecting stroke of the cursive allographs and is included because it forms a strong perceptual cue for these allographs.
The software tool to teach the system the allographs displays a writing pattern with small circle markers on each stroke. The markers indicating the initial and final strokes of an allograph and the name of the allograph are successively clicked by using the mouse. Occasionally, N-gram names have to be entered by means of the keyboard. The naming of N-grams is needed when two allographs regularly 'melt' together because of increased writing speed. Typical fused digrams in Dutch handwriting are , , and in many writers.
Once the procedure is running smoothly it takes on average 5 s per allograph to teach the system. After the teaching phase all allographs and their names can be made visible in order to assure that no mistakes have been made. Two handwritings were trained. The first handwriting (Writer A) was a neat constant-size handwriting and was trained incrementally up to 1671 prototypes by exposing the system to characters it could not discriminate or recognize well. The average number of strokes per allograph was 4.7. The second handwriting (Writer B) was a normal handwriting with considerable variation of allograph sizes with words. The allographs were trained from an a priori determined story of 240 words with low word frequencies. The script contained 1366 allographs (a posteriori), the average number of strokes per allograph being 2.9. The total script was written in 16 minutes.
8 Conclusion
It seems that the complex software system requires a powerful machine. A system inspired by the human motor system and the human perceptual system may seem to confine itself artificially. However, we see that the architecture is a very modular one (vertical modularity) and allows parallel modules (horizontal modularity). Problems can be very well located in one or two levels of the system. As such it seems that can be extended and tested relatively easily. The word hypothesization based on varying-length input sequences containing meaningless objects (e.g., connecting strokes) is currently a problem that has been solved only partially. It is to be hoped that robust artificial neural network models, handling noisy sequential data of unbounded lenght, will evolve in the future. This capability will be of special importance in languages like, e.g., German and Dutch, where nouns and prepositions plus nouns may be concatenated to form strings that are unlikely to be an entry in a standard lexicon.
9 References
Crossman, E.R.F.W. (1959). A theory of the acquisition of a speed-skill. Ergonomics, 1959, 2, 153-166.
Hayes, F. (1989). True notebook computing arrives. Byte,14, 94-95.
Jordan, M.I. (1985). The learning of representations for sequential performance. Doctoral dissertation. University of California, San Diego, pp. 1-160.
Kohonen, T. (1984). Self-organisation and associative memory. Berlin: Springer.
Kondo, S. (1989). A model of the handwriting process and stroke-structure of character-figures. In R. Plamondon, C.Y. Suen, M. Simner (Eds.), Computer recognition and human production of handwriting (pp. 103-118). Singapore: World Scientific.
Maarse, F.J., Janssen, H.J.J., & Dexel, F. (1988). A special pen for an XY tablet. In F.J. Maarse, L.J.M. Mulder, W.P.B. Sjouw & A.E. Akkerman (Eds.), Computers in psychology: Methods, instrumentation, and psychodiagnostics (pp. 133-139). Amsterdam: Swets & Zeitlinger.
Maarse, F.J., Meulenbroek, R.G.J., Teulings, H.-L., & Thomassen, A.J.W.M. (1987). Computational measures for ballisticity in handwriting. In R. Plamondon, C.Y. Suen, J.-G. Deschênes, & G. Poulin (Eds.), Proceedings of the Third International Symposium on Handwriting and Computer Applications (pp. 16-18). Montreal: Ecole Polytechnique.
Maarse, F.J., Schomaker, L.R.B., & Teulings, H.L., (1988). Automatic identification of writers. In G.C. Van der Veer & G. Mulder (Eds.), Human-Computer Interaction: Psychonomic Aspects (pp. 353-360). New York: Springer.
Maarse, F.J., & Thomassen, A.J.W.M. (1983). Produced and perceived writing slant: Difference between up and down strokes. Acta Psychologica, 54, 131-147.
Maier, M. (1986). Separating characters in scripted documents. 8th International Conference on Pattern recognition (ISBN: 0-8186-0742-4), 1056-1058.
Morasso, P., Kennedy, J., Antonj, E., Di Marco, S., & Dordoni, M. (1990). Self-organisation of an allograph lexicon. International Joint Conference on Neural Networks, Lisbon, March.
Morasso, P., Neural models of cursive script handwriting (1989). International Joint Conference on Neural Networks, Washington, DC, June.
Pick, H.L., Jr., & Teulings, H.L. (1983). Geometric transformations of handwriting as a function of instruction and feedback. Acta Psychologica, 54, 327-340.
Plamondon, R., & Maarse, F.J. (1989). An evaluation of motor models of handwriting. IEEE Transactions on Systems, Man and Cybernetics, 19, 1060-1072.
Skrzypek, J., & Hoffman, J. (1989). Visual recognition of script characters: Neural network architectures. Technical report UCLA MPL TR 89-10, Computer Science Department University of California, Los Angeles
Srihari, S.N., & Bozinovic, R.M. (1987). A multi-level perception approach to reading cursive script. Artificial Intelligence, 33, 217-255.
Stornetta, W.S., Hogg, T., & Huberman, B.A. (1987). A dynamical approach to temporal pattern processing Proceedings of the IEEE conference on Neural Information Processing Systems, Denver.
Tappert, C. (1986). An adaptive system for handwriting recognition. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 185-198). Amsterdam: North-Holland.
Tappert, C.C., Suen, C.Y., & Wakahara, T. (1988). On-line handwriting recognition: A survey. IEEE, 1123-1132.
Teulings, H.L., Schomaker, L.R.B., Gerritsen, J., Drexler, H., & Albers, M. (1990). An on-line handwriting-recognition system based on unreliable modules. In R. Plamondon, & G. Leedham (Eds.), Computer Processing of Handwriting (pp. 167-185). Singapore: World Scientific.
Teulings, H.L., Schomaker, L.R.B., Morasso, P., & Thomassen, A.J.W.M. (1987). Handwriting-analysis system. In R. Plamondon, C.Y. Suen, J.-G. Deschênes, & G. Poulin (Eds.), Proceedings of the Third International Symposium on Handwriting and Computer Applications (pp. 181-183). Montreal: Ecole Polytechnique.
Teulings, H.L., Schomaker, L.R.B., & Maarse, F.J. (1988). Automatic handwriting recognition and the keyboardless personal computer. In F.J. Maarse, L.J.M. Mulder, W.P.B. Sjouw, & A.E. Akkerman (Eds.), Computers in psychology: Methods, instrumentation, and psychodiagnostics (pp. 62-66). Amsterdam: Swets & Zeitlinger.
Teulings, H.L., Thomassen, A.J.W.M., & Van Galen, G.P. (1983). Preparation of partly precued handwriting movements: The size of movement units in writing. Acta Psychologica, 54, 165-177.
Teulings, H.L., Thomassen, A.J.W.M., & Van Galen, G.P. (1986). Invariants in handwriting: The information contained in a motor program. In H.S.R. Kao, G.P. Van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary Research in Handwriting pp. 305-315. Amsterdam: Elsevier.
Teulings, H.L., & Maarse, F.J. (1984). Digital recording and processing of handwriting movements. Human Movement Science, 3, 193-217.
Thomassen, A.J.W.M., Teulings, H.-L., Schomaker, L.R.B., Morasso, P., & Kennedy, J. (1988). Towards the implementation of cursive-script understanding in an online handwriting-recognition system. In Commission of the European Communities: D.G. XIII (Ed.), ESPRIT '88: Putting the technology to use. Part 1 (pp. 628-639). Amsterdam: North-Holland.
Thomassen, A.J.W.M., & Teulings, H.L. (1985). Time, size, and shape in handwriting: Exploring spatio-temporal relationships at different levels. In J.A. Michon & J.B. Jackson (Eds.), Time, mind, and behavior (pp. 253-263). Heidelberg: Springer.
Watrous, R., & Shastri, L. (1987). Learning phonetic features using connectionist networks Proceedings of the 1987 IJCAI, Milano (pp. 851-854).
Abraham 14, 24
Abramowitz 90, 109
Adams 5-6, 24, 152, 176
Agarwal 45, 47, 137, 150
Akazawa 131
Akkerman 110, 210-211
Albers 23, 27, 211
Allum 5, 24
Andreewsky 76
Antonj 132, 210
Asada 53, 76, 83, 109
Asanuma 116, 131, 149-150, 154, 176
Baier 82, 109
Ballard 21, 24, 116, 131, 135-136, 150, 157, 176
Barto 177
Bauer 176
Beech 25
Beek 14-16, 24, 86, 109
Bendat 24, 32-33, 46-47, 90-91, 109
Beni 24, 190
Bigland 116, 131
Bisiacchi 76
Bizzi 6, 9, 13, 24, 84, 109, 182, 190
Blinowska 137, 150
Boerhout 28
Bootsma 12, 24
Bozinovic 196, 210
Brady 110, 181, 190
Brault 75-76
Broadbent 22, 24
Brosch 176
Brown 36, 47
Bullock 152, 162, 176-177
Cannet 137, 150
Carpenter 157, 176
Chua 14, 26, 152, 177
Connor 158, 178
Coolen 125, 131, 136, 150, 156, 176, 182, 190
Crane 82, 109
Crick 116, 131, 149-150, 154, 176
Crossman 5, 24, 210
De Luca 5, 24, 137, 150, 157, 177
Deinet 82-84, 109
Denes 76
Denier van der Gon 6, 8, 24, 28, 51, 54, 65, 74-76
Desa 19, 24, 181, 190
Deschênes 76-77, 109-110, 190, 210-211
Dexel 99, 110, 198, 210
Di Marco 132, 210
Dijkstra 6, 8, 24
Dimond 5, 8, 24
Dooijes 17, 24, 38, 47, 51, 53, 56, 62, 76, 82, 86, 89, 106, 109
Dordoni 132, 210
Drexler 23, 27, 211
Eckhorn 157, 176
Edelman 106, 109, 115-117, 131-132
Ellis 10, 24, 52, 76
Elman 154, 177
Estes 154, 176
Fairbanks 4, 24
Fisher 177
Fitch 15, 27
Flash 7, 52, 76, 106, 109, 115, 131
Flude 10, 24
Fogelman-Soulié 27
Freeman 132, 157, 178
Freund 5, 24
Fujii 131
Furukawa 109
Gelatt 131
Gerritsen 23, 27, 211
Gibson 12-13, 24
Gielen 125, 131, 136, 150, 156, 176, 182, 190
Gisbergen 8, 25
Gold 38, 47, 62, 77
Goodman 25
Gottlieb 137, 150
Grimby 7, 25
Grossberg 127, 131, 152, 157, 162, 176
Grossman 154, 176
Hackwood 24, 190
Hale 82, 109
Hannerz 7, 25
Harley 23, 25
Harnad 115, 131
Hartmann 154, 176
Hayes 196, 210
Hedman 7, 25
Hinton 122, 124, 126, 131-132, 136-137, 139, 150, 153, 156, 176-177
Hoffman 204, 210
Hogan 13, 25, 82-85, 105, 109, 182, 190
Hogg 178, 211
Hollerbach 15, 19, 25, 49-52, 54, 76, 106, 109-110, 152, 176, 190
Hoosain 26-28, 31, 47, 50, 77, 110-111, 178, 211
Hopfield 123-126, 131-132, 153, 156, 176, 182
Houk 152, 177
Huberman 178, 211
Hull 25
Hulstijn 9, 15, 25, 61, 76, 105, 109, 152, 176
Hussong 109
Hylkema 9, 28, 178
Inbar 137, 150
Ivaldi 74-76, 84, 86, 110, 132, 182, 190
Janssen 99, 110, 198, 210
Jeffress 25
Johnson 110, 190
Jones 5, 25, 116, 132, 137, 150
Jordan 155, 157-158, 162-163, 176-177, 204, 210
Kanerva 149-150
Kanosue 116, 131
Kao 26-28, 31, 47, 50, 77, 85, 109-111, 178, 211
Kawato 107, 109
Kelso 7, 13-15, 25-27
Kennedy 27, 132, 210-211
Keuss 18, 26
Kirkpatrick 124-125, 131
Knoll 9, 27, 178
Kobayashi 82, 109
Kohonen 127-129, 131, 157, 177, 183-184, 186-188, 190, 195, 197, 202-203, 205, 210
Kondo 199, 210
Koster 51, 54, 77
Kraepelin 85, 109
Kretschmer 85, 110
Kruse 176
Lago 116, 132, 137, 150
Lamarche 51, 53, 77
Laming 7, 25
Lashley 6, 25
Lee 15, 25, 109
Linke 109
Lin 19, 25, 182, 190
Lippold 4, 25, 116, 131
Lorette 82, 110
Luh 19, 25, 182, 190
Maarse 17, 26, 33, 47, 49-52, 56, 62, 67, 76-77, 82, 85-86, 88, 92, 99, 110-111, 164, 178, 196-198, 200-201, 210-211
Maier 196, 208, 210
Mannaerts 18, 26
Marr 114, 132
Marsden 7, 26
Martin 176
Mason 83, 110, 190
McClelland 23, 26, 131-132, 136, 150, 154, 176-177
McIntosh 7, 26
Melton 176
Merton 7, 26
Meulenbroek 9, 28, 52, 76, 108, 178, 210
Milgram 137, 150
Mille 177
Mohler 7, 28
Monsell 9, 27, 178
Moore 177
Morasso 6, 9, 23-24, 26-27, 53, 56, 74-77, 84, 86, 109-110, 115, 129, 132, 182, 190, 202, 208, 210-211
Morton 7, 26
Mulder 110, 210-211
Mullins 27
Munk 176
Mussa 74-76, 84, 86, 110, 132, 182, 190
Niez 116, 132, 154, 177
Norman 154-155, 161-162, 177
O'Regan 25
Olson 7, 26
Ostrem 82, 109
Paganini 82, 109
Parker 14, 26, 152, 177
Paul 19, 26
Pellionisz 135, 150, 182, 191
Peretto 116, 132, 154, 177
Perkel 154, 164, 177-178
Pfeifer 27
Pick 2, 200, 210
Piersol 24, 32-33, 46-47, 90-91, 109
Plamondon 17, 26-27, 51, 53, 56, 75-77, 80, 82, 85, 87, 108-111, 177, 190, 198, 210-211
Polanyi 23, 26
Polit 9, 24, 84, 109
Poulin 76-77, 109-110, 190, 210-211
Pratt 158, 177
Rabiner 36, 38, 47, 62, 77
Rack 5, 13, 26, 105, 110
Raibert 52, 77
Reddish 15, 25
Redfearn 4, 26
Reeke 115-117, 132
Regan 32, 47
Reitboeck 176
Requin 24, 27, 47, 190
Rieger 109
Roberts 5, 26
Robinson 155, 177
Roebroek 8, 25
Rosenthal 5, 26
Roth 19, 24, 181, 190
Ruggiero 76, 132
Ruijgrok 125, 131
Rumelhart 23, 26, 122, 131-132, 136-137, 139, 150, 153-156, 161-162, 176-177
Sahar 19, 25
Saltzman 13-15, 26
Sanders 12, 15, 26, 113, 132
Schmidt 7, 20, 26
Schomaker 5, 10-11, 15, 18-19, 23, 26-27, 31, 33, 47, 49-51, 53, 72, 74, 76-77, 80, 82, 86, 88, 90, 92, 101, 106, 108, 110-111, 116, 137, 150-152, 155, 157, 177-179, 181, 183, 191, 194, 196, 200-201, 210-211
Schopman 131, 150, 190
Schreter 27
Schulman 177
Segundo 177
Sejnowski 124, 126, 131, 153, 176
Semenza 76
Shastri 155-156, 178, 204, 211
Shaw 14, 24
Shek 109
Simner 51, 76-77, 111, 177, 210
Singh 177
Sivak 7, 26
Sjouw 110, 210-211
Skarda 157, 178
Skrzypek 204, 210
Slotine 53, 76, 83, 109
Sloviter 158, 178
Smolensky 115-116, 132
Smyth 178
Southard 25
Srihari 196, 210
Steels 23, 27
Stegun 90, 109
Steinwachs 85, 111
Stein 123, 132
Stelmach 6, 15, 24, 27, 47, 105, 111, 190
Sternberg 9, 27, 113, 133, 152-153, 178
Stornetta 154, 178, 204, 211
Strackee 76
Sudhakar 45, 47
Suen 51, 76-77, 109-111, 177, 190, 210-211
Suhash 45, 47
Sutton 177
Suzuki 109
Tagliasco 76, 182, 190
Tam 154, 178
Tappert 196, 208, 211
Teder 109
Ten Hoopen 18, 26
Terzuolo 5, 26, 35, 47
Teulings 15, 23, 27, 32-33, 47, 49-52, 54, 56, 58, 65, 75-77, 82, 86, 105-106, 110-111, 164, 177-178, 194, 196-198, 200-204, 208, 210-211
Thomassen 15, 23, 26-27, 31-33, 47, 49-51, 54, 72, 74, 77, 86, 88, 92, 101, 106, 110-111, 177, 198, 200, 202, 210-211
Thuring 54, 65, 74-76
Torras i Genís 116, 133, 154, 157, 164, 173-174, 178
Tuller 15, 27
Turvey 15, 27
Van Boxtel 5, 27, 53, 77, 90, 111, 137, 150, 157, 178
Van der Plaats 10-11, 26
Van Doorn 116
Van Galen 9, 15, 25-28, 31, 33, 47, 50, 52, 61, 76-77, 105, 109-111, 116, 152, 173, 176, 178, 183, 191, 211
Van Opstal 8, 25
Vecchi 131
Verroust 137, 150
Viviani 35, 47
Von der Malsburg 154, 178
Von Hámos 4, 28
Vredenbregt 51, 54, 77
Wadman 6, 9, 28
Wakahara 211
Watrous 155-156, 178, 204, 211
Werbos 177
Wiener 2, 28
Williams 122, 132, 137, 139, 150, 153, 156, 177-178
Witteveen 59, 77
Wright 9, 27, 178
Wurtz 7, 28
Yoshida 131
Young 10, 24
Summary
This study concerns the processes that take place from the
moment that a writer wants to write down a given word, until one
can inspect the finished result. What types of transformation are
needed, going from planned word to muscle contraction? The approach
followed is based on the assumption that new insights can be gained by
trying to build a working generative computer model of handwriting.
Chapter 1 deals with the theoretical aspects of modeling processes of
motor control. Many viewpoints reveal essential aspects of motor control,
but no single viewpoint will suffice to provide the building blocks
for a working model of handwriting production. Hence, a "vertical"
approach is taken, adopting the necessary components for the different
processing levels from cybernetics, cognitive motor theory, robotics,
and connectionism. Chapter 2 discusses an important aspect of the
pen-tip kinematics during cursive writing: How reproducible are
replications of writing movements recorded on different occasions?
Only if movements are actually reproducible, it makes sense to develop
a handwriting production model. This chapter forms the starting point
of the development of the model, since it shows that invariance and
replicatability are indeed present in movement patterns with the
duration of at least a single letter. Chapter 3 presents a computer
model of handwriting. One of the basic problems that have to be solved
is concerned with the transformation of discrete entities, i.e., the
symbolic representation of a planned letter shape (allograph), into a
continuous multi-dimensional time function, i.e., the movement of the
pen tip. This problem is tackled with the assumption that strokes are
the basic segments in handwriting. The number of strokes is known
to exert a quantized influence on the reaction time in the programming
of handwriting movements by a human writer. In the model, a
parsimonious parametrization of the strokes is used, which is based on
transforming a shape factor into differential timing. Based on
findings which indicate that the motor programs in cursive handwriting
involve movement patterns of this size, the model aims
at handwriting production that proceeds letter by letter.
Consequently, a grammar,
dubbed the Cursive Connections Grammar, providing rules for generating
connecting strokes between two planned letters is proposed. Up to this
point in the thesis, the model has only been concerned with the
kinematics of the pen-tip movement. However, the important question
may be asked if movement kinematics are the only domain which is
controlled by "motor programs" for handwriting production. Apart from
the intrinsic forces that generate movement, the pen is in contact
with the writing surface, yielding normal force and friction. Thus, in
Chapter 4, a kinetic aspect of writing is studied: What happens to
axial pen force during the production of several types of movement
patterns and what are the implications for movement control as
specified in the working model? It appears that pen-force fluctuations
are not a passive biomechanical phenomenon. Also, in most writers, the
pen-force
pattern during letters is invariant across replications, which
supports the notion that pen force is a separate domain. Pen-force control
and compliance appear to be embedded in the "motor programs" for letter
production, in an idiosyncratic, writer-dependent fashion. In Chapter 5, a
change of perspective takes place. It is noted that there are some
limitations inherent to a symbolical modeling approach, especially
with respect to low-level processes in handwriting control. A review
of basic artificial neural-network models is presented and their
potential use both in modeling handwriting movement control and in
handwriting recognition is assessed. In the following chapters, three
basic issues are raised with respect to motor modeling: The coding of
quantity, the representation of time, and the representation of the
effector system by neurally inspired models. Chapter 6 deals with the
representation of quantity. Differences between basic types of coding
are described: Firing-rate control, value-unit coding, and
recruitment. In Chapter 7, the representation of time in neural
systems and the learning of handwriting time functions are addressed. A
new neural-network model of the production of time functions is
proposed, consisting of an ensemble of neuron-interneuron spike
oscillators. The last of the three neural modeling experiments is
described in Chapter 8 and concerns the problems of the representation
of an effector. A planar arm with three degrees of freedom is used
to compare two neural-network models and their ability to learn
the transformation of two-dimensional target-movement patterns into
three-dimensional joint-angle patterns, i.e., the inverse-kinematics problem.
The neural-network models are trained by random generation of arm movements
("motor babbling"). A final interesting and relevant problem is computer
recognition of handwriting movements which is the focus of Chapter 9. Part of
the knowledge gathered thus far in simulating the production of cursive
handwriting and in neural-network proved to be helpful in the automatic
recognition of handwriting movements as recorded on-line with a digitizing
tablet. An algorithm is proposed that performs recognition by actively
constructing letter (allograph) hypotheses on the basis of chains of individual
strokes, instead of storing prototypical allographs and performing template
matching.
Samenvatting
Een verticale benadering van de modelvorming
op het gebied van de menselijke motoriek
Dit proefschrift heeft betrekking op de processen die plaatsvinden vanaf het moment dat de schrijver een gegeven woord wil opschrijven, tot het moment dat hij of zij het schrijfproduct kan inspecteren. Welke soorten transformaties zijn er vereist, van woord tot spiercontractie? De hier gevolgde benadering is gebaseerd op de assumptie dat nieuwe inzichten kunnen worden verkregen door een werkend, generatief computermodel van het cursieve schrijven te ontwikkelen. Hoofdstuk 1 behandelt de theoretische aspecten van modelvorming op het gebied van motorische processen. Meerdere gezichtspunten verduidelijken essentiële aspecten van de motoriek, maar er is momenteel geen enkel theoretisch gezichtspunt dat de bouwstenen kan aandragen voor een werkend (computer-)model van de schrijfbeweging. Daarom wordt in dit proefschrift een "verticale" aanpak gevolgd, waarbij de noodzakelijke componenten van de verschillende verwerkingsniveaus ontleend zijn aan de cybernetica, de cognitieve motorische theorie, de robotica en het connectionisme. Hoofdstuk 2 beschrijft een belangrijk aspect van de kinematica van de penpunt gedurende het cursieve schrijven: hoe reproduceerbaar zijn replicaties van schrijfbewegingen die op verschillende momenten geregistreerd zijn? Immers, alleen als de bewegingspatronen feitelijk reproduceerbaar zijn, heeft het zin om een model van de productie van handschrift te ontwikkelen. Dit hoofdstuk is een aanknopingspunt voor het ontwikkelen van een dergelijk model omdat wordt aangetoond dat er een hoge mate van invariantie en repliceerbaarheid is van bewegingspatronen met een duur van minstens een letter. Hoofdstuk 3 beschrijft een computationeel model van het schrijven. Eén van de basisproblemen die opgelost moeten worden betreft de transformatie van discrete entiteiten (de symbolische representaties van "geplande" lettervormen of allografen), naar een continue, meerdimensionele tijdfunctie (de bewegingen van de penpunt). Dit probleem wordt benaderd door uit te gaan van de bevinding dat er fundamentele eenheden in de schrijfbeweging zijn, te weten "halen", waarvan het aantal een gekwantiseerde invloed heeft op de reactietijd bij het programmeren van schrijfbewegingen door de menselijke schrijver. In het model wordt een spaarzame parametrisatie van de haal gebruikt, die gebaseerd is op de transformatie van een vormfactor naar differentiële "timing". Het model richt zich op de productie van handschrift die letter voor letter voortschrijdt. Dit uitgangspunt wordt ondersteund door bevindingen dat de "motor programma's" in het cursieve schrijven de omvang van een letter hebben. Een grammatica (Cursive Connections Grammar) wordt geïntroduceerd, die de regels bevat voor het genereren van verbindingshalen tussen twee opeenvolgende "geplande" letters. Tot op dit punt in het proefschrift is alleen de kinematica van de penpunt aan de orde geweest. Men kan zich afvragen of dit het enige domein is dat gestuurd wordt door "motor programma's". Nog afgezien van de intrinsieke krachten die nodig zijn voor het genereren van de beweging, geldt dat de pen in contact is met het schrijfoppervlak, hetgeen leidt tot een normaalkracht, en een daaruit voortvloeiende wrijving gedurende de beweging. Daarom wordt in hoofdstuk 4 een kinetisch (d.w.z. krachts-) aspect van het schrijven bestudeerd. Wat gebeurt er met de axiale penkracht (pendruk) gedurende de productie van verschillende typen van bewegingspatronen en wat zijn de implicaties voor de sturing van de penbeweging zoals die in het werkend model worden gespecificeerd? Het blijkt dat de fluctuaties in de axiale penkracht geen passief biomechanisch fenomeen zijn. Tegelijkertijd echter zijn bij de meeste schrijvers de krachtspatronen gedurende het schrijven van een bepaalde letter reproduceerbaar over meerdere replicaties. Deze bevinding is een ondersteuning van de opvatting dat penkracht apart geregeld wordt vanuit het centrale zenuwstelsel. Het lijkt erop dat de krachtsregeling in de "motor programma's" is verdisconteerd, op een voor elke schrijver idiosyncratische wijze. In hoofdstuk 5 treedt een verandering van perspectief op. Enige inherente beperkingen van het in hoofdstuk 3 gehanteerde symbolische model, met name wat betreft de lage-orde aspecten van de motoriek worden behandeld vanuit de optiek van het connectionisme (kunstmatige neurale netwerkmodellen). Er wordt een overzicht gepresenteerd van een aantal bestaande neurale netwerkmodellen. Tevens wordt hun potentiëel belang voor de modelvorming op het gebied van de motoriek van het schrijven bekeken. In de hierop volgende hoofdstukken worden drie fundamentele onderwerpen behandeld met betrekking tot netwerkmodellen van de motoriek: de codering van kwantiteit, de representatie van tijd en de representatie van het effectorsysteem. Hoofdstuk 6 behandelt de representatie van kwantiteit. De verschillen tussen drie bekende neurofysiologische typen codering (vuurfrequentiesturing, topologische "value unit" codering en recrutering) worden beschreven in de context van het leren van een non-lineaire functie door een meerlaagsperceptron. In hoofdstuk 7 komt de representatie van tijd in neurale netwerken en het leren van handschrift-tijdfuncties aan de orde. Een nieuw neuraal netwerkmodel voor de productie van temporele patronen wordt geïntroduceerd, bestaande uit een ensemble van neuron-interneuron puls-oscillatoren. In hoofdstuk 8 komt vervolgens de representatie van het effectorsysteem aan de orde. Hier wordt uitgegaan van een eenvoudige twee-dimensionele schrijfarm met drie vrijheidsgraden. Er wordt onderzocht in welke mate twee verschillende neurale netwerkmodellen in staat zijn om de transformatie van "geplande" twee-dimensionele penpuntbewegingen naar een drie-dimensionele tijdfunctie van gewrichtshoeken te leren. Dit wordt gedaan op basis van een willekeurig verlopend leerproces ("motor babbling"). Hoofdstuk 9 betreft de herkenning van schrijfbewegingen met behulp van de computer. Een deel van het eerder beschreven onderzoek bleek zeer wel bruikbaar te zijn bij de automatische herkenning van handschrift zoals dit ön-line" met een schrijftablet door de computer ingelezen wordt. Er wordt een algoritme voorgesteld waarin de herkenning van allografen berust op een actieve constructie van letterhypothesen op basis van de binnenkomende halenreeksen, in plaats van een passieve vormvergelijking met eerder opgeslagen gehele lettervormen.
Publications
Maarse, F.J., Schomaker, L.R.B., & Teulings, H.-L. (1988).
Automatic identification of writers.
In G.C. van der Veer & G. Mulder (Eds.),
Human-Computer Interaction: Psychonomic Aspects
(pp. 353-360). New York: Springer.
Maarse, F.J., Schomaker, L.R.B., & Teulings, H.-L. (1985). Automatische identificatie van schrijvers. [Abstract]. Congresbundel Mens-Computer-Interactie Conferentie, Amsterdam, p. 22.
Maarse, F.J., Schomaker, L.R.B., & Teulings, H.-L. (1986). Kenmerkende verschillen in individueel schrijfgedrag: Automatische identificatie van schrijvers. Nederlands Tijdschrift voor de Psychologie, 41, 41-47.
Maarse, F.J., Schomaker, L.R.B., & Thomassen, A.J.W.M. (1986). The influence of changes in the effector coordinate systems on handwriting movements. In H.S.R. Kao, G.P. van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 33-46). Amsterdam: North-Holland.
Schomaker, L.R.B. (1988). Robotica en menselijke motoriek. In P.J.G. Keuss, G. Ten Hoopen & A.A.J. Mannaerts (Eds.), Psychonomische Publikaties: Menselijke Motoriek (117-140). Amsterdam: Swets en Zeitlinger.
Schomaker, L.R.B. (1989) Een betaalbaar systeem voor het aanbieden van toon en spraakstimuli in psychologische experimenten. Psychologie en Computers, 6(3), 79-83.
Schomaker, L.R.B. (1990). Neural Network Models of Temporal Pattern Generation. [Abstract]. Conference on Sequencing and Timing of Human Movement. Wassenaar (The Netherlands): NIAS, p. 27.
Schomaker, L.R.B. (1991). A neural-oscillator model of temporal pattern generation. Human Movement Science, 11, 181-192.
Schomaker, L.R.B. & Adriaansen, Th. (1984) Kermit, een algemeen communicatieprogramma. Psychologie en Computers, 1(3), 20-25.
Schomaker, L.R.B. & Plamondon, R. (1990). The Relation between Pen Force and Pen-Point Kinematics in Handwriting. Biological Cybernetics, 63, 277-289.
Schomaker, L.R.B., Thomassen, A.J.W.M., & Teulings, H.-L. (1987). A computational model of cursive handwriting. In R. Plamondon, C.Y. Suen, J.-G. Deschênes, & G. Poulin (Eds.), Proceedings of the Third International Symposium on Handwriting and Computer Applications (pp. 5-7). Montreal: Ecole Polytechnique.
Schomaker, L.R.B., Thomassen, A.J.W.M., & Teulings, H.-L. (1989). A computational model of cursive handwriting. In R. PLamondon, C.Y. Suen, & M.L. Simner (Eds.), Computer Recognition and Human Production of Handwriting (pp. 153-177). Singapore: World Scientific.
Schomaker, L.R.B., & Teulings, H.-L. (1990). A Handwriting Recognition System based on the Properties and Architectures of the Human Motor System. Proceedings of the International Workshop on Frontiers in Handwriting Recognition (IWFHR). (pp. 195-211). Montreal: CENPARMI Concordia.
Schomaker, L.R.B., & Thomassen, A.J.W.M. (1986). On the use and limitations of averaging handwriting signals. In H.S.R. Kao, G.P. van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 225-238). Amsterdam: North-Holland.
Teulings, H.-L., Schomaker, L.R.B., Morasso, P., & Thomassen, A.J.W.M. (1987). Handwriting-analysis system. In R. Plamondon, C.Y. Suen, J.-G. Deschênes, & G. Poulin (Eds.), Proceedings of the Third International Symposium on Handwriting and Computer Applications (pp. 181-183). Montreal: Ecole Polytechnique.
Teulings, H.-L., Schomaker, L.R.B., & Maarse, F.J. (1986). Automatische herkenning van handschrift en de PC zonder toetsenbord. [Abstract]. Tweede Workshop Computers in de Psychologie: Programma en Abstracts. Nijmegen, p. 16.
Teulings, H.-L., Thomassen, A.J.W.M., Schomaker, L.R.B., & Morasso, P. (1987). Experimental protocol for cursive script acquisition: The use of motor information for the automatic recognition of cursive script. Report 3.1.2., ESPRIT Project 419.
Teulings, H.L., Schomaker, L.R.B., Gerritsen, J., Drexler, H., & Albers, M. (1990). An on-line handwriting-recognition system based on unreliable modules. In R. Plamondon, & G. Leedham (Eds.), Computer Processing of Handwriting (pp. 167-185). Singapore: World Scientific.
Thomassen, A.J.W.M, Teulings, H.-L., Schomaker, L.B.R., Morasso, P., & Kennedy, J. (1988) Towards the implementation of cursive-script understanding in an online handwriting-recognition system. In D.G. XIII (Ed.), ESPRIT '88: Putting the technology to use (pp. 628-639). Amsterdam: North-Holland.
Thomassen, A.J.W.M., Teulings H.-L., & Schomaker, L.R.B. (1985). Toegang tot de computer door middel van handschrift. [Abstract]. Congresbundel Mens-Computer-Interactie Conferentie, Amsterdam, pp. 23-24.
Thomassen, A.J.W.M., Teulings, H.-L. & Schomaker, L.R.B. (1988). Experimentation and simulation in handwriting research. Proceedings of the 24th International Congress of Psychology. Full-paper abstract (F636), Sydney.
Thomassen, A.J.W.M., Teulings, H.-L., Schomaker, L.R.B., & Morasso, P. (1987). Experimentation and modelling in the study of cursive script. Report, Phase I of ESPRIT Project 419, Image and movement understanding.
Thomassen, A.J.W.M., Teulings, H.-L., & Schomaker, L.R.B. (1988). Real-time processing of cursive writing and sketched graphics. In G.C. van der Veer & G. Mulder (Eds.), Human-Computer Interaction: Psychonomic Aspects (pp. 334-352). New York: Springer.
Thomassen, A.J.W.M., & Schomaker, L.R.B. (1986). Between-letter context effects in handwriting trajectories. In H.S.R. Kao, G.P. van Galen, & R. Hoosain (Eds.), Graphonomics: Contemporary research in handwriting (pp. 253-272). Amsterdam: North-Holland.
Van Boxtel, A., Goudswaard, P., & Schomaker, L.R.B. (1983). Recording methods for the frontalis surface EMG. Psychophysiology, 20, 475.
Van Boxtel, A., Goudswaard, P., & Schomaker, L.R.B. (1984). Amplitude and bandwidth of the frontalis surface EMG: Effects of electrode parameters. Psychophysiology, 21, 699-707.
Van Boxtel, A., Schomaker, L.R.B., Goudswaard, P., & Molen, G.M. van der (1983). Power spectra of surface EMG of facial and jaw-elevator muscles in relation to motor unit firing rate and fatigue. Electroencephalography and Clinical Neurophysiology, 56, 191.
Van Boxtel, A., & Schomaker, L.R.B. (1983). Motor unit firing rate during static contraction indicated by the surface EMG power spectrum. IEEE Transactions on Biomedical Engineering, 30, 601-609.
Van Boxtel, A., & Schomaker, L.R.B. (1984). Influence of motor unit firing statistics on the median frequency of the EMG power spectrum. European Journal of Applied Physiology, 52, 207-213.
Van Galen, G.P. & Schomaker, L.R.B. (1990). Fitts' Law as a Low-Pass Filter Effect of Muscle Stifness. [Abstract]. Conference on Sequencing and Timing of Human Movement. Wassenaar (The Netherlands): NIAS, p. 18.
Van Galen, G.P. & Schomaker, L.R.B. (in press). Fitts' Law as a Low-Pass Filter Effect of Muscle Stifness. Human Movement Science, x(x), xxx-xxx.
Van Galen, G.P., Van Doorn, R.R.A., & Schomaker, L.R.B. (1988). Effects of motor programming on the power spectral density function of writing movements. Journal of Experimental Psychology, 16, 755-765.
Vingerhoets, A.J.H.M., & Schomaker, L.R.B. (1984). Emotional fainting: its physiological and psychological aspects. In C.D. Spielberger et al., Stress and Anxiety.
Vingerhoets, A.J.H.M., & Schomaker, L.R.B. (1984). Flauwvallen als stressreactie. Gedrag, 12, 46-59.
Curriculum vitae
Lambertus Richardus Bernardus Schomaker werd geboren op 19 februari 1957 te
Nijmegen. Van 1969 tot 1975 volgde hij het gymnasium B aan het Odulphuslyceum
te Tilburg. Vanaf september 1975 studeerde hij psychologie aan de Katholiek
Hogeschool Tilburg. In 1982 werkte hij als studentassistent in een project
betreffende de habituatie van de oogknipreflex. In januari 1983 studeerde hij
cum laude af, met als met als specialisatie fysiologische psychologie. De
afstudeerscriptie betrof de relatie tussen EMG en accelerogram bij het optreden
van tremoren in gelaatspieren. In 1983 en 1984 vervulde hij zijn vervangende
dienst als onderzoeksassistent bij de Vakgroep Fysiologische Psychologie aan de
Katholiek Hogeschool Tilburg. Sinds april 1984 is hij werkzaam bij de Vakgroep
Psychologische Functieleer aan de Katholieke Universiteit Nijmegen, van 1984
tot 1988 binnen het ZWO-project Ëen model van de schrijfbeweging", sinds 1988
binnen het Esprit project Ïmage and movement understanding" (Project 419). In
1989 was hij onder meer werkzaam in het oprichten van een consortium voor een
tweede Esprit project, betreffende de ontwikkeling van een ëlectronic notepad
computer", dat inmiddels is goedgekeurd: "Papyrus" (Project 5204). In 1991 zal
hij betrokken zijn bij de organisatie van de 5th Meeting of the International
Graphonomics Society en de 2nd International Workshop on Frontiers in
Handwriting Recognition.
Glossary
- abduction, wrist 85
- acceleration 21, 23, 38, 59, 87, 179
- activation of an allograph 202
- activation patterns, decoding 136
- activation, faulty 138
- activation, maximimum 165
- activation, motor unit 135
- activation, multi-unit binary 136
- activation, multi-unit recruitment 136
- activation, multi-unit topology 136
- activation, muscle 16
- activation, myoelectric 155
- activation, single-unit (SA) 136
- adaptation 17, 122, 180
- adaptive compliance control 180
- adaptive resonance theory 126
- adduction, wrist 85
- adult writer 105
- agonist 39, 106
- allographic context 76
- allograph 6, 41, 55-56, 58, 62-63, 68-69, 76, 192-193, 196, 200-202, 205-206
- alpha motoneuron pool 140
- alpha motoneuron 135
- alpha-motoneurons 135
- alphabet 167
- amplitude 22
- analog regeneration 55
- analog-to-digital (a/d) problem 115
- analog 12-13, 64, 88, 115, 120
- angles, preferred 93
- angles 93, 179, 181, 183-184, 186
- angle 44, 77, 83, 85, 87-88, 91, 99, 105, 107, 134, 182-183, 185
- angular velocity 87-88, 91-92, 98, 105
- annealing phase 126
- annealing schedule 126
- annealing, simulated 6, 126
- antagonist 39, 106
- anticipation errors 156
- anticipation of next stroke 48
- anticipation, planning 28
- anticipatory lowering of co-contraction 106
- apf 82
- artificial neural network 107
- ascenders 64-65, 89, 197, 204
- association, memory 115
- association 22, 116, 120, 123, 125
- asynchronous firing 135
- asynchronous update 125
- attractor 22
- autonomous compliance control 180
- autonomous non-linear oscillator 155
- autonomous state transitions 155
- autonomy 17, 19, 23-24, 28, 164
- averaging handwriting signals 37
- axial pen force (apf) 82
- axon 133, 135, 161
- babbling, chaotic 164
- babbling, motor 183
- back propagation 6
- ballistic movements 67
- ballistic movement 181, 194, 196
- ballistic stroke 67
- ballistical stroke production 57
- bandwidth 92, 195
- baseline 44, 75, 191
- bdf 84
- behaviorism 9-10
- behaviorist 10
- bigrams 76
- binary coding 134, 136, 143, 147
- binary threshold function 136
- biological system 114, 116, 120, 133, 136-137, 149, 155-156, 181
- biomechanical coupling 87
- biomechanical hypothesis 85
- biomechanical origin of pen force 6
- biomechanical processes 5
- biomechanical 6, 81-85, 87, 100, 105-106
- biomechanics, muscle 28
- biomechanics 20, 106, 156
- biphasic 106
- bipolar operating range 13
- blindfolded handwriting 19
- blindfolded writing 18
- blunt stroke ending 60
- body space 21
- boxology 19
- brittleness 115
- buffering 22, 155
- bundle 117, 135, 147
- burst 15, 162
- calligrapher 101
- cartesian space, low-dimensional 25
- cartesian 55, 59, 76, 88, 91, 106, 182
- categorical 115
- categorization 67
- categorized 115
- ccg 62, 191
- cellular columns 127
- cellular column 127, 157
- cell 117, 120-121, 154, 161, 192, 200
- central nervous system 16-17, 24
- cerebellar 77
- cerebellum 14, 24
- cerebral cortex 127, 134
- cerebral level 16
- chain 10, 17, 84, 157
- channel 165, 167
- chaos 21
- chaotic babbling 164
- characters 53, 191, 197, 204, 206
- classification of allographs 202
- classification 120, 128, 154, 198
- classified 39, 101
- classify 39, 117, 128, 156
- clockwise circling 89-90, 94-95
- clockwise ending 43, 60
- clockwise turn 39, 43
- clockwise 96-99, 105
- cluster of neurons 135
- cluster 134-135
- co-contraction 17, 182
- coarse coding 134
- coarticulation 156, 160
- coding accuracy 136, 144
- coding of quantity 6, 133
- coding of time 158
- coding robustness 136
- coding schemes 134
- coding scheme 136
- coding, binary 134
- coding, coarse 134
- coding, conjunctive 134
- coding, firing rate 133
- coding, flying spot 165, 172
- coding, mixed recruitment and rate coding 141
- coding, polar coordinates 76
- coding, recruitment 133
- coding, topological 133
- coding, value units 133
- coding, word contour 204
- coding 134-135
- cognitive activity in processing visual feedback 18
- cognitive approach 19
- cognitive function 113
- cognitive motor theory 5, 9, 17-18, 21, 24, 28
- cognitive psychology 9
- cognitive science 24, 29
- cognitive 28, 53, 113, 115-117, 155, 157
- cognitivism 27
- cognitivist approach 19
- cognitivist 113
- coherence 82, 87-88, 92, 96-100, 105-107
- collinearity 147
- collision avoidance 26, 179
- collision 57, 204-205
- column, cell 127
- compliance control 180
- compliance 27, 81, 83-84, 179-180
- compliant 84
- computation, parallel 28
- computational aspects of motor control 9
- computational model 53, 55, 63
- computational resources 24
- computational speed 26
- computational 53, 55, 114-115, 155, 158, 170, 180, 192, 197, 202
- computation 76, 120, 156, 167, 181, 194, 198
- computer recognition of handwriting movements 7
- configuration of a Task network 21
- configuration of a new feature extractor 134
- configuration of a pattern generator 162
- configuration of minimum potential energy 182
- configuration of oscillators 22, 162
- configuration, dynamical system 24
- conjunctive coding 134
- connecting of strokes 6
- connecting strokes 41-43, 202, 205-206
- connecting stroke 39, 46, 67, 205
- connection strength 117, 122, 163
- connectionism and motor control 179
- connectionism, and motor control 154
- connectionism 5, 9, 27-29, 113, 116, 129, 133
- connectionist 77
- connectivity 125, 127-128, 157, 167, 200
- connector codes 69
- consonants 204
- constraint 25, 86, 124-125, 147, 165
- context 39-41, 53-54, 56, 63-64, 75-76, 106, 196, 198-199, 205
- contour coding of words 204
- contour coding 205
- contour 204-205
- contraction levels, ratio of 27
- contraction of bubble radius 128
- convolution window 91
- coordinate system, effector 91
- coordinate transformation problem 25
- coordinate 54, 76
- coordinative structure gearing 164
- coriolis force 27
- coriolis 56
- corpus 64, 76
- correlation matrix 73
- correlation 71-75, 82, 87, 92, 95, 99-102, 105-107, 128, 166, 198-199
- cortex, cerebral 127, 134
- cortex 14-15, 24, 28
- cortical connectivity 127
- counterclockwise circling 90
- counterclockwise ending 60
- counterclockwise turn 39, 43, 60
- covariance 108, 166
- cursive allographs 55, 205
- cursive characters, isolated 167
- cursive connections grammar 6, 62, 69, 191
- cursive handwriting, modeling 24
- cursive handwriting, recognition of 191-192
- cursive handwriting 5, 22, 58, 90, 164
- cursive script recognition 192
- cursive script representation 106
- cursive script, model 115
- cursive script 29, 65, 82, 95, 128
- cursive style 89
- cursive words 63
- cursive writing 5
- cursive-script recognition 77
- cursive 55
- curvature 49, 53, 61-62, 67, 88, 92, 105, 195
- cybernetical 155
- cybernetics 5, 9-12, 14-19, 24, 28, 54
- cybernetic 12
- damped, critically 13
- damped 59
- damping 12-13, 57
- deafferentiation 15
- decay, exponential 62, 165
- deceleration 59, 76
- decircularize 50
- decomposition 107
- deconvolution 196
- degree of freedom 183
- degrees of freedom problem 155
- degrees of freedom, body (bdf) 84, 180
- degrees of freedom, intra-corporal 84
- degrees of freedom, statistical 92
- degrees of freedom, task (tdf) 84, 180
- degrees of freedom 25-26, 84, 181
- degrees of limited freedom 183
- delay time 14
- delay, axonal 117
- delay, cortico-muscular 28
- delay, neural transmission 27
- delay, transmission 13
- delay 12-15, 28, 57, 60-61, 68, 87, 157, 165
- delta rule, generalized 121
- delta rule 119, 121, 166
- depolarization 161
- derivative 121-122
- descenders 62
- descender 64-65, 197, 204
- differentiable 120
- differential equations 12, 115
- differential 53, 127, 155
- differentiated 64, 91
- differentiation 39, 44, 49, 91-92, 107, 193-194
- differentiator 91, 107
- digital regeneration 55
- digital-to-analog (d/a) problem 115
- digital 54
- digitized 64, 193
- digitizer 88-89, 93, 167, 191, 193, 195, 198
- digitizing 192, 194
- digram 18, 201
- digraph 76
- dimension 117, 154, 156
- dirac pulses 23-24
- discrete characters 205
- discrete entities 191
- discrete events 57, 164
- discrete motor actions 157
- discrete movement segments 54
- discrete pattern units 22
- discrete patterns 14, 170
- discrete sequences 159
- discrete states 43
- discrete strokes, chaining of 59
- discrete-to-continuous transform 53
- discreteness of symbols 27
- displacement 12, 21, 23, 38-39, 60-61, 63-64, 82-83, 86-88, 91-92, 99-101, 105-106, 133, 165-166, 179, 191, 194-195
- distal 85, 127
- distributed single-unit dynamics 158
- distributed 89, 127-128, 138, 160-161, 197
- distribution of available time 62
- distribution, uniform 165, 167
- distribution 53, 101, 123, 126, 137, 140, 165, 167, 172, 185, 199
- disturbance 13, 17, 20
- dots, in recognition 204
- dots, positions of 65
- dots 164
- dottings 69
- doubling errors 172
- doubling of a movement segment 158, 172
- down stroke 39, 42, 44-46, 48, 101
- downstroke, duration 53
- downward 87
- drawing a random scribble 25
- drawing 82, 87-88, 91, 94, 106
- duration and size 53
- duration and stiffness 182
- duration of relaxation phase 156
- duration variability 37-38
- duration, down stroke 53
- duration, motor unit twitch 15
- duration, stroke 41
- duration, varying-duration patterns 154
- dynamic programming 77
- dynamic range 89, 134, 136, 138-140
- dynamic time warping 42
- dynamic vs static 21
- dynamical system configuration 24
- dynamical system description 24
- dynamics 9, 20-24, 38, 57, 76, 107, 155, 158, 180
- dynamic 21
- ecological approach 19, 21, 23
- ecological perspective 20, 24
- ecological 57
- editing, graphical 67-68, 202
- editing 69
- editor 167
- effector configuration 84
- effector coordinate system 91
- effector systems 87
- effector system 129, 155, 164, 179
- effector 7, 11-14, 17, 24-28, 53-54, 56-58, 76, 84, 86-87, 99, 146, 155, 179-184, 186
- einstellung 18
- elastic energy field (pef) 182
- elastic energy field 182-183
- elastic energy potential function 86
- elastic energy 85
- elasticity 20, 23, 27
- emergence 200
- emergent consequences 5
- end effector 81, 164
- end of pattern 162
- end plates 135
- endpoint 179, 196
- ensemble averaging 37-38
- ensemble of neurons 161
- ensemble 38, 42, 92, 102, 161-163, 172
- entrainment 161
- equilibrium states 20
- equilibrium theory 183
- equilibrium 20, 23, 85-86, 126, 182
- ergonomical 193
- ergonomic 205
- escapement 23
- esprit, project P419 37, 55, 82, 133, 154, 179, 192
- esprit 2, 29, 37, 55, 77, 82, 108, 128, 133, 154, 179, 192
- estimator 92, 197-198
- excitability 57
- excitation 57, 116
- excitatory connection 162
- excitatory 116, 128
- execution of pattern 162
- expert 117
- exponential 197
- exteroceptive 57
- fault tolerance 136
- feature vector quantization 183
- feature vectors, prototypical 202
- feature vectors, sequence of 202
- feedback loop 11
- feedback, first-order 11
- feedback, visual 16
- feedback 11-18, 20, 27-28, 57-58, 105, 107, 114, 127, 155, 164, 170
- feedforward networks 182
- feedforward 17-18, 105, 154, 158-159, 167, 201
- fiber 15
- filter, recursive 67, 139
- filter 44, 59, 64, 139, 194
- fine tuning 136
- finger activity 91
- finite impulse response 49
- fir filter 64
- firing frequency, virtual 135
- firing rate as "certainty" value 134
- firing rate, virtual 120, 133
- firing, asynchronous 135
- fir 64
- flying spot coding 141, 165, 172
- force and compliance 27
- force control 9, 106
- force invariance 23
- force range 27
- force tdf 84
- force, normal 6
- forced 86
- forces 6, 27, 56, 76, 179
- force 6, 15, 21, 27, 57, 76, 81-88, 91, 95, 99-100, 105-107, 164, 179-180, 182
- forcing pulses, kicks 23
- forcing 23, 57-58, 172
- forearm 85, 87-89, 93
- forefinger 83
- formal production system 77
- fourier function 23
- fourier 39, 49-50, 92, 195
- frequencies 69, 161, 206
- frequency 22-23, 39, 50, 53, 64, 87-89, 91-92, 94, 98, 105, 116, 134, 161, 167, 194-195
- frictional 84
- friction 6, 23, 27, 57, 84, 86, 94, 106
- gain of a feedback system 12
- gain of momentum term 139
- gain, loop 13
- gain 13, 16, 50, 95, 162, 182
- ganglia 24
- gannet 22
- generalization 116, 165
- generalized delta rule 122
- generalize 196
- generation vs regeneration 5, 55
- generator 54, 61, 70, 76, 161-162
- gestaakt 89, 100, 102-104
- gibbs 195
- gibsonian perspective 19-20
- gibsonian 155
- golgi, tendon sensor 14
- graceful degradation 116
- graded 163
- gradient 139
- grammar, cursive connections 6, 62, 191
- granularity 115, 134
- graphemes 56, 63
- graphical editing 67-68
- graphical simulation 27
- graphical 202
- graphics 76
- graphonomics 37, 54
- graphs 202
- gravitation 27
- grip 27
- hamming 125
- hand anatomy 84
- hand muscles 13
- hand stiffness 106
- handprint 193, 205
- hands 57
- handwriting generator 63
- handwriting model 10
- handwriting movements, recognition of 191-192
- handwriting variability 196
- handwriting, averaging kinematics signals 37
- handwriting, human reading of 192
- handwriting, kinematics vs kinetics 82
- handwritings 206
- handwriting 5-6, 9-10, 12, 14, 17-18, 21-22, 24, 26-29, 35, 37-39, 41-45, 48-49, 53-68, 71, 75-77, 81-84, 86-89, 92, 94-95, 105-107, 114, 129, 133, 135, 154-156, 158, 167, 170, 180, 191-198, 202, 205-206
- hand 13, 15, 17, 25-26, 44, 56-57, 77, 83-84, 87, 89, 91, 155, 180, 202
- harmonics 94
- harmonic 94
- hexagonal 200
- hidden layers 120, 122
- hidden layer 122, 159
- hidden units 121, 140, 146-147, 150, 165
- hidden unit 139
- hierarchy 64
- histogram 64-65
- homothetic 41-42, 49
- homunculus 14, 115
- human information processing system 113
- human motor system 55
- human operator 26
- hunting 13
- hysteresis 12, 57, 94
- impedance 27, 82-84, 86, 105-107
- impulse response differentiator 44
- impulse response 24
- impulse 49, 59, 61, 68, 159
- industrial robot 181
- inertia 13
- information processing system 155
- inhibited 127
- inhibition 161
- inhibitory connection 162
- inhibitory 116, 127
- inhibits 157
- innervate 135
- innervating 135
- input excitation 140
- integrate 154
- integrating 67
- integration 60
- intention 56, 86
- inter-neurons 116
- inter-neuron 163, 165
- interception 180
- interconnections 161
- interoceptive 57
- interpolated 67
- interpolation 49, 179
- intra-personal space 180
- intracorporal 56
- invariance in planar pen-tip kinematics 35
- invariance, force 23
- invariance, spatial 23
- invariance, temporal 23
- invariance 5, 35, 56, 76, 172, 198
- invariant 56-57, 192, 196, 199
- inverse dynamics 107, 134
- inverse kinematics by neural networks 179
- inverse kinematics 25-27, 155, 179
- inverse kinetics 27
- inverse 39, 50, 57, 76, 106, 127, 181-183
- isometric 57
- isotonic 86
- iterations 28, 156, 200
- iwfhr 192
- jacobian 26, 181-182
- jerk, minimum 115
- jitter 38, 105, 158
- joint angles 25-27
- joint angle 20, 25, 134, 182-183, 185
- joint space, high-dimensional 25
- joint 20, 27, 56-57, 76, 84, 179-186
- juggling 23-24
- keyboard 157, 193, 198, 206
- kicks 23
- kinematic movement parameters 10
- kinematical 81, 155
- kinematics and kinetics 81-82
- kinematics model 53, 55
- kinematics, averaging handwriting signals 37
- kinematics, inverse 25-26, 155
- kinematics, pen-tip 5
- kinematics 6, 21, 23-24, 26-27, 35, 57, 76, 81-84, 86, 94-95, 98-100, 105-106, 179-183
- kinematic 21, 35, 76, 82, 84, 105, 129, 155
- kinetics 21, 27, 81-82, 155, 179-180
- kinetic 6, 155
- knowledge of results 14
- kohonen network 202
- kohonen 126-128, 161, 183-186, 192, 194, 199-200
- kr 14
- labeling allographs in recognition 201-202
- lagrange weights 91
- layer 117-118, 120-121, 123, 127, 140-141, 146-147, 159-160, 165
- learned 125-126, 139, 159-160
- learning a continuous function 7
- learning a static sinusoid transform 135
- learning ability, human 107
- learning cursive script 106
- learning curves 146
- learning curve 147
- learning of cursive handwriting 5
- learning task dynamics 22
- learning to write 86
- learning vector quantization (lvq) 183
- learning 14, 17-18, 116-117, 119-126, 128, 133, 135, 139, 144, 146-149, 154, 156, 159, 161, 165-167, 170, 172, 183, 186, 192, 194, 200, 205
- learn 147, 159, 162, 197, 205
- lesions 77
- limb anatomy 182
- limb 20, 183
- limited information capacity 161
- linear array of units 140
- linear classifier, cascaded 118
- linear classifier 117-118
- linear detrending 49
- linear elasticity 23
- linear independence 119
- linear regression 91
- linear writing movements 85
- linearity of the base line 18
- linearity 134
- linearly separable object classes 117
- lineation 62-66, 68, 75, 191
- linguistic frequencies 205
- linguistic 56, 202
- links, arm 25, 27
- links, auto-recurrent 158-159
- locomotion 180
- low-pass filtering 13
- low-pass filter 64
- low-pass 38, 67, 88, 166, 170, 194
- manipulator system 25
- manipulator 26-27, 107, 181-182
- mass-spring system 180
- matrix inversion 114
- mechanical arm 25
- mechanical damping 57
- mechanical impedance 27, 82
- mechanical structure 25
- mechanical transfer function 182
- mechanics 21, 57, 124
- membrane 161, 163, 173
- memory association 115
- mexican hat 127
- minimum jerk 115
- misalignment, stroke 67
- model, cursive script 115
- model, kinematics 53, 55
- modeled 160, 172
- modeling 14, 17-18, 22, 27-28, 35, 106, 113, 115-117, 129, 154, 156-157, 159, 161, 172
- models of handwriting 55
- models, neural networks 113
- modularity, degree of 25
- modularity 24-25, 198, 206
- modular 113, 193, 206
- modulating mass-spring oscillators 58
- modulating oscillatory behavior 161
- modulation, amplitude and phase 58
- module 76-77, 113-114, 156, 205
- momentum impulse 59
- momentum 59-62, 67-68, 70-71, 75, 139, 165-166
- monolithic entities 27
- monolithic 115
- monopolar operating range 13
- monopolar 200
- motoneuron, alpha 15
- motoneuron, firing frequencies 135
- motoneuron 13, 135
- motor babbling 183
- motor context 63
- motor control, workshop 179
- motor control 5-7, 9-10, 12-19, 24, 26-29, 58, 85, 129, 133-134, 154-156, 159, 179-183
- motor modeling 6
- motor skill 180
- motor system 155
- motor unit contraction 57
- motor unit twitch 15
- motor unit 13, 15, 135
- movement duration 165
- movement segment 172
- multiplicative synapses 157
- muscle activation patterns 18
- muscle activation 17, 27
- muscle contraction 5, 13, 16, 53, 85, 182, 194
- muscle fiber 15, 135
- muscle length 17
- muscle relaxation 13
- muscle spindles 15
- muscle spindle 13, 135
- muscle stretch 135
- muscle system, virtual 167
- muscle 13, 15-16, 38, 53, 57, 85, 135, 182
- muscular 81, 85
- myoelectric activation 155
- neocortex 157
- nerve 135
- nervous system 57, 154, 161
- nervous 57, 86-87
- network, multi-layer 133
- network 116-117, 119-121, 123-125, 127-129, 134-135, 137, 144-148, 150, 154, 156-159, 163-172, 183-185, 192, 194, 198, 200, 202
- neural architecture 114
- neural feedback loop 105
- neural information processing system 57
- neural network model of handwriting 135
- neural network model, of temporal pattern generation 154
- neural network models 6, 113
- neural network model 133, 154
- neural network simulations 6
- neural network simulation 77
- neural network, self-organizing 199
- neural networks 179
- neural pattern production 163
- neural processes 5
- neural self-organization 6
- neural system 161
- neurally inspired models 9
- neurally oriented model of handwriting 28
- neurally 164
- neuraxis 28
- neuroelectric delay 13
- neuroelectric 15
- neuromechanical delay 13
- neuromuscular feedback 20
- neuron activation level 116
- neuron-inhibitory interneuron pair (nin) 161
- neurons 28, 116-117, 133-135, 156, 161, 165
- neuron 116, 122, 133-135, 149, 154, 161-163, 165, 172, 174
- newtonian equation of movement 21-22
- nias 82, 179
- nici 192-193
- nin oscillator 166, 172
- noise in neural information processing 57
- noise in neuro-muscular force control 106
- noise reduction 38
- noise, "thermal" 126
- noise, baseline level 115
- noise 37-39, 58, 106, 116, 133, 135, 147, 157-158, 162, 164-165, 167, 194-195
- non-linear mapping by threshold distribution 134
- normal pen force (npf) 83
- normalization 37, 39, 43-44, 46, 48-49, 102, 192-193, 196-198, 200
- normalize 39
- normalizing time 42
- normalizing 43, 48, 124, 196
- npf 83
- nwo 2, 37, 55, 82
- oblique 88
- obstacle in car driving 16
- obstacles 57
- obstacle 180
- oculomotor control 14
- oculomotor system 16
- one-shot response 14
- open-loop approach 18
- open-loop control 16
- operational 156
- operations 113, 147, 194
- operator 67
- orientation normalization 197
- orientation of a force 27
- orientation of baseline 18
- orientation of end effector 26
- orientation 18, 44, 58, 64, 84, 181, 183, 191, 197-198
- oriented 155, 161
- oscillate 13, 136
- oscillating 89
- oscillations 12, 124, 195
- oscillation 13, 19-20, 23-24, 54, 58, 61, 98, 159, 172
- oscillator configuration 22, 162
- oscillator model of handwriting 22
- oscillator, NiN 161
- oscillator, non-linear 155
- oscillator, pulse 135
- oscillator, spike 161
- oscillatory behavior 22
- oscillatory mode 155
- oscillatory tasks 22
- oscillatory task 23
- oscillatory 54, 155, 161
- oscillator 22, 24, 53-54, 58, 86, 154-155, 161-164
- overcompensates 106
- overruled 105
- overshoots 66
- pace modulation 172
- pace 88, 172
- pacing 61
- papyrus 193
- parameterization method 60
- parameterization 55, 58, 61, 68, 70, 75
- parameterized 55, 61
- parameterize 60
- parameterizing 70
- parametrization, of strokes 6
- passband 195
- pattern completion 123
- pdp 43, 88, 161
- pef, potential elastic energy field 182
- pen angle variations 99
- pen angle 84-85, 99
- pen force (apf) trend during trials 95
- pen force 6, 27, 81-82
- pen lift 62, 69
- pen pressure 6, 81-82
- pen tilt angle 99
- pen tilt 84
- pen traces 193
- pencil 11, 14
- pen 6, 12, 44, 57-58, 64, 69, 81-88, 91, 99, 105-107, 180, 192-195, 199
- perceptron 117-118, 149, 156, 158, 162, 172, 183-184, 201
- perceptual input 16, 24, 28
- perceptual trace 14
- perceptual 16, 76, 115, 117, 123, 154, 194-195, 204-206
- performance 113, 147, 180, 194-195, 197, 200, 202, 204, 206
- periodic attractor 22
- periodicity 87, 98, 105
- periods 69, 91
- peripheral 18
- phase 22
- phasor 53
- pitch envelope 63
- planar pen-tip kinematics 35
- planar 57-58, 76, 85, 88, 106, 183
- plane 77, 81, 83-84
- plasticity 147
- polyarticular 84
- polynomial function 23
- preprocessing 64, 67
- presentation 118, 121, 124, 127, 156
- pressing 182
- pressure 43-44, 64, 82-83, 85, 87-88, 105-106, 195
- proprioceptive input 12, 16-17, 24
- proprioceptive 57
- prototypical feature vectors 202
- psychomotor control 25, 29
- psychomotor 82
- pulse oscillator ensemble model 172
- pulse oscillator networks, training 161
- pulse oscillator network 165
- pulse oscillators, stochastic 116
- pulse oscillator 135, 161, 172
- pulse 154, 156, 161-162, 164
- pushing 83
- quantization 115, 126-128, 192, 194, 198-200
- quantized 193-194, 196, 198, 200-201
- radial abduction 82, 105
- radius 101, 200
- ramp 158
- random 37-39, 49, 56, 93, 126, 140, 183
- rate coding 133, 146-147, 150
- reaching 167, 184
- reaction time 6, 16, 113
- reader, human, of handwriting 192
- reader 193
- reading: human, of handwriting 192
- receptor 146-147
- recoded 204
- recognition systems 193
- recognition system 205
- recognition 9, 29, 39, 42, 157-159, 191-193, 195-196, 198-199, 201-202, 204-205
- recognizer 192
- recognizing 29, 193
- reconstruct 114, 199-200
- record 41, 49-50, 93-94, 100
- recruited 135, 140
- recruitment and activation 141
- recruitment and virtual firing rate 141
- recruitment coding 133-135, 146-147, 149
- recruitment 57, 134-136, 138, 140-141, 144, 147-151, 161
- recurrent links 159
- recurrent network 154, 164
- recurrent 118, 127-128, 154, 158-162, 164, 167-170, 172, 174, 201
- recursion 28, 118
- recursive application of ccg 62
- recursive filter-like functionality 165
- recursive filtering 158
- recursive filter 67, 139
- reflex arc, mono-synaptic 13, 16
- reflex 13-14, 17
- refrigerator 12
- regeneration vs generation 5, 55
- regulated 86
- regulates 106
- regulating 84
- regulation 106, 181
- relaxation, minimum 165
- relaxation 123, 126, 156
- relaxed 89, 167, 173
- relax 172-173
- repertoire of oscillators 24
- repertoire 197
- repetition 158, 204
- repetitive pattern 164
- repetitive 58, 154
- replicatability of movements 35
- replicatability 5, 53, 82, 100-101, 105-106
- replicatable relation between apf and displacement 105
- replicate 101
- replication 35, 72
- representation a quantity 135
- representation of allographs 6
- representation of continuous functions 6
- representation of letter shapes 9
- representation of movement 19, 27
- representation of quantity 7, 129
- representation of the effector system 129
- representation of time and sequence 129
- representation of time 6-7, 154
- representation stability, temporal 135
- representation, cursive script 106
- representation, of quantity 133
- representation, of the effector system 179
- representation 6, 28, 35, 38, 40-42, 48, 53, 56-58, 77, 114-115, 127, 133, 144, 146-147, 157-160, 164, 179, 181, 183, 185, 196, 198, 201
- reprogram 76
- reservoirs 156
- resonance 161
- resonators 161
- response speed 13
- response 10, 14, 43-44, 49, 89-91, 156, 158
- reversals 100
- righthanded 64
- rms 140, 165, 170
- robot system 84
- robot, industrial 181
- robotics, industrial 26
- robotics 5, 28, 179
- robot 26-27, 84
- robustness 116, 172
- rosenberg 177
- rotated 44
- rotational 84
- rotation 39, 64, 76, 84
- sample record 37
- sample, of an on-line recorded word 202
- sample 38, 49-50, 59-61, 66, 68-71, 75, 93-94, 100, 197
- sampling 12, 64, 88, 167, 195
- scribbles 87-89, 95, 98
- scribble 25
- scribbling 58, 90, 96-98
- script 55, 114, 192, 196, 206
- segmental and supra-segmental drive 135
- segmentation of handwriting 29
- segmentation of word into allographs 193
- segmentation 61, 67, 192-195, 200, 205
- segmented 38, 44, 68, 191, 194
- segmenting 42, 205
- segment 39, 41-44, 49, 83, 94-95, 102, 135, 155, 158, 183, 199, 205
- sejnowski 177
- selector channel 165
- selector line 165
- selector 165, 167
- semantic 56
- sensor systems 87
- sensory information 13
- sensory input 17
- sensory signals 16
- sensory-to-motor representation transform 129
- sensory 12, 128-129, 134, 155, 164
- sensor 11-13
- sentence 56
- sequence of feature vectors 202
- sequence of operations 63
- sequence of stroke parameters 62
- sequence 41-42, 55, 128-129, 157-160, 191, 197, 200-201
- sequential data 206
- sequential 35, 126, 157, 202
- serial 56, 88, 158, 196
- series 38, 95, 167
- servo control 19
- servo systems 11
- shaping 125, 155-156, 159-162, 164, 172, 182
- sharp stroke ending 60
- sigmoid 146
- signal-to-noise ratio (snr) 198
- signal-to-noise ratio 140
- signature 82-83
- simulated annealing 6, 126
- simulation, generative 9
- simulation, graphical 27
- simulations 116
- simulation 5, 37-38, 49, 55, 58, 113, 115-116, 129, 154, 167, 169-171, 191
- sine 39, 140
- single-unit activation 146-147
- singularity of jacobian 26
- singularity 114
- sinus oscillator 58
- sinusoid 60, 135, 144, 146
- sinus 136
- size and duration 53
- skeleto-muscular 82, 85
- smoothing window 92
- smoothing 92, 139, 165
- smoothness 61, 94
- solution space 202
- space 55-57, 59-60, 69, 84, 101, 115, 117, 159, 167, 179, 182-183, 198, 200-202
- spacing 39, 114
- spatial invariance 23
- spatial tdf 84
- spatialized 154, 157-158, 165
- spatially 86
- spatial 35, 37-38, 40-42, 48-49, 53, 55-62, 64-65, 67, 70, 75-76, 84, 86, 89, 98, 105, 164, 179-180, 186, 193, 199-200
- speaker 63
- speaking 13, 16
- speak 83, 123, 183
- spectral characteristics 38
- spectral 39, 82, 92, 94, 96-97, 158, 161, 194-195
- spectra 92, 94, 96-98
- spectrum 39, 53, 88, 92, 94, 98, 107, 194
- speech 13, 39, 42, 63, 128, 156-158, 160, 201, 204
- speed 15, 88, 105, 135, 147, 149, 158-159, 164-166, 172, 193, 198, 206
- spherical wrist 26, 181
- spike oscillator 135
- spike 163, 166
- spiking 161-162
- spinal 135
- spine 15
- spin 123
- splines 49
- squashing 166
- start of pattern 162
- state transitions 155
- stationary 37, 93
- steersman 10
- stepwise 62, 120, 202
- stiffness control 17
- stiffness matrix 105
- stiffness, hand 106
- stiffness 21, 23, 27, 84, 86, 105-106, 181-182
- stimuli 90, 156
- stimulus 10, 14, 91
- stochastic pulse generator 161
- stochastic renewal pulse oscillators 116
- stochastically 125
- stochastic 114, 116, 156
- storage 125
- stored 85, 88, 201
- store 159, 165, 172
- storing 202
- stroke duration parameter 61
- stroke duration 41
- stroke generator 62
- stroke modeling 61
- stroke parameterization process 62
- stroke shape parameter 61
- strokes 6, 15, 18, 38-39, 41, 43, 46, 48-49, 53, 55-57, 59-62, 66-67, 70, 72-76, 83, 87, 99-100, 105-106, 128, 157, 164, 192-202, 205-206
- stroke 14, 18, 37-49, 53, 55, 57-62, 67-68, 70-74, 76, 83, 87-88, 101, 191-192, 194-195, 198-202, 204, 206
- stuttering 164
- style 85-87
- styloideus 89
- stylus 43, 88, 106, 193
- subjects 18, 43, 46, 53, 64, 82-83, 87-88, 92, 94, 98-103, 105-106
- subject 14-15, 37, 39, 41-42, 44-49, 65, 70-71, 76, 85, 88-89, 91-95, 99-104, 144, 198
- subsegments 49
- subsystem 12, 105
- summation, statistical 13
- summing 163
- sums 44
- symbolic information processing systems 115
- symbolic letter description 62
- symbolic models 28
- symbolic stage 61
- symbolical 53
- symbolic 6, 27-28, 55, 63, 66-67, 69, 76, 113-115, 155, 157, 192
- symbols 10, 27-28, 55, 58, 62, 115, 191, 196
- symbol 62, 115
- synapses 157
- synaptic input 118
- synaptic 116, 118-119, 123
- synchronisation 161
- synchronization 101
- synchronously 64, 195
- synchronous 120, 125
- synergetics 155
- synergism 87
- syntactical 56
- syntactic 117
- syntax 56
- synthesis 77
- synthetic 59
- system configuration 162
- system state 155, 159-160
- systems dynamics approach 9, 19, 21, 24
- systems theory 9, 86
- systems 54
- table lookup in inverse kinematics 182
- table search 144
- tablet 43-44, 64, 67, 88-89, 99
- tactile input 12, 24
- tangential 61, 83, 87-88, 91-92, 98, 105
- tapering 92
- target letter shape 12
- target shape 12
- target value 11, 14
- target, in aiming movements 15, 17
- targeting 56, 155
- targets 17
- target 17, 55-56, 58, 61, 85, 106, 119, 121, 128, 139-140, 146, 155, 158, 164-166, 170-171, 181-182, 196, 202
- task dynamics, learning 22
- task network 21
- task space 21
- task type 180
- task, binary decision 16
- task, oscillatory 23
- tasks, cyclic 22
- tasks, oscillatory 22
- tasks, patterning 22
- tasks 27, 57, 180-182
- task 18, 43, 48, 56, 81, 84, 88, 107, 114, 155, 164, 180, 182-183, 205
- tdf 84
- teacher 128
- teaching a continuous function 133
- teaching the recognition system 205
- teaching 107, 149, 156, 160, 183, 206
- teach 107, 154, 161, 167, 205-206
- temperature 126
- templates 49
- template 49, 201
- temporal flow model 158
- temporal invariance 23
- temporal pattern generation, neural network model 154
- temporally 85, 157
- temporal 14, 37, 53-54, 56, 75, 98, 115, 154, 157-159, 161, 172, 192, 201
- tempo 62
- tendon sensor, Golgi 14
- tendon 85
- tesselation 200
- texture 193
- thermal 126
- thermionic valve 25
- thermometer coding 140
- thermostats 12
- thickness 81, 83-84, 86
- thresholds 122, 125, 134
- threshold 116, 119-120, 122-124, 142, 147, 158, 162, 173, 195
- thumb 105
- tilt 195
- time alignment 42, 77
- time domain 193
- time function 115
- time in neural network models 156
- time reference 38, 41
- time series 39
- time warping, dynamic 42
- time warping 42, 77
- time window 108, 158, 195
- time, allocation of 55
- times 15, 35, 46, 48-49, 54, 60, 83, 88, 102, 147, 181-182, 200
- timing 16, 53, 58, 60, 164
- tolerance 135
- tolerant 136
- tolerate 164
- topologically 157
- topological 58, 127, 134, 136, 141, 143, 154, 158, 196
- topologies 196
- topology 126, 133, 136, 140-142, 157, 196
- torques 27, 84, 179-180, 183
- torque 27, 180, 182
- trace of allographs 202
- trace, perceptual 14
- traced 48
- trace 35, 76, 81, 83-84, 86, 114, 155, 157, 171, 192, 198, 200, 205
- tracking behavior 14
- tracking hypothesis of handwriting control 14
- track 100, 113
- trainability 160
- trainable 160-162
- trained 157, 183, 192, 201, 206
- training pulse oscillator networks 161
- training time 151
- training 140, 147, 151, 159, 165-168, 170, 172, 196, 200, 202
- train 158
- trajectories 35, 54, 56, 86
- trajectory formation 9, 27
- trajectory 24-27, 55-59, 61, 76, 83-86, 105-107, 167, 182, 195
- transducer 43, 83, 88, 195
- transfer function, dynamic 12
- transfer function, static and dynamic 117
- transfer function, static 12
- transfer function 20, 59, 91, 116, 120, 134, 139, 182
- transformation problems 120
- transformation, discrete to continuous 6
- transformation, sensory-to-motor representation 129
- transformations 56-57, 69, 120
- transformation 56, 114, 128, 154, 180-183
- transformed 56, 84, 88, 91-92, 107
- transforming 53, 158-159
- transforms 115, 157, 195
- transform 39, 49-50, 53, 92, 100, 115, 118, 120, 197
- transients 38-39
- transient 37-38
- transistor 25
- transition, from clockwise to counterclockwise 39
- transitions 43, 76, 88
- transition 44, 61, 64, 76, 192, 195, 201
- translated 124
- translate 58
- translational 84
- translation 55
- translator 128
- transmission delays, intra-cortical 28
- transmission delay 13
- transmission 13, 105, 125, 157-159
- transport 180
- transputers 198
- tremor 13
- trend 95, 102
- triangularly 59
- triangular 39, 59
- triggering 161
- triggers 38
- trigrams 202
- truncation 140
- tuning, fine 136
- tuning 136, 141, 158, 172
- turing 28
- twitch, motor unit 15
- twitches 57
- twitch 15
- typing 156-158, 170, 172, 193
- ulnae 89
- ulnar 89
- undamped 13
- undershoots 66
- unit activation function, binary threshold 118
- unit activation function, linear 118
- unit activation function, sigmoidal 121
- unit activation level 116
- unit activation, dynamic range 139
- unit activation 120-122
- units, of action 22
- units 35-36, 41, 57-58, 92, 94, 104, 116-126, 128, 134, 136-138, 140-142, 144-147, 149-151, 156-159, 165, 167, 172, 186, 193-194, 200
- unit 39, 59, 61, 92, 116-127, 157-158, 161, 164
- unsupervised 126, 128
- unthinned 193
- update, of unit activities, asynchronous 125
- update 133
- updating 120, 123-125
- upstroke 10
- valley 86
- value unit coding 133-135, 147, 149
- value units 134
- values 44, 49, 61, 87, 93, 98-100, 105, 117, 120, 123-124, 126, 128, 134, 136, 139, 141, 144, 147, 156-157, 164-165, 167, 170, 180, 186, 192, 194, 199
- value 38, 74, 77, 82, 87, 93, 98-100, 102, 106, 108, 118, 121, 125, 127, 157, 160, 164, 200
- variabilities 196
- variability, handwriting 196
- variability 39, 41-43, 46, 48-49, 57, 116, 196
- variables 82, 92, 105, 114, 129, 140, 165, 173, 180
- variable 48, 65, 81, 83, 86, 105-106, 146, 160, 172
- variance 38, 43, 82, 87, 93, 95, 99, 102, 105, 107, 197
- variants 56, 196
- variant 196
- variations 39, 41, 43, 58, 68, 82-87, 91, 105-107, 195, 198, 200
- variation 38, 83, 86-87, 99, 102, 114, 196, 206
- vaxstation 88, 167
- vax 144
- vectorial 192
- vectors 117, 119, 122, 197, 199-201
- vector 64, 117-118, 120-121, 125-128, 180-181, 192, 198-200
- velocities 49, 94
- velocity signals 44
- velocity 12, 21, 23, 35-36, 38-39, 41, 43, 47-49, 55, 58-61, 64, 68, 70, 75, 83, 87-88, 91-92, 96-98, 105, 165, 168, 179-180, 194-195
- ventral 135
- verification 82-83
- vertical 35, 58-61, 64, 67, 70, 72, 74-75, 83, 89, 91, 99-101, 106, 127, 133, 168, 195, 197-199, 206
- vestibular input 17
- vestibular 76
- vhs 193
- visco-elasticity 13, 20
- visco-elastic 13
- viscoelastic 85
- viscosity 21, 23
- viscous friction 23
- visual cortex 15
- visual feedback 16, 18
- visual input 12, 17-18, 24
- visually 199
- visual 18, 57, 99, 170, 181, 193, 198
- viterbi 200-201
- walking 22
- weighed 116, 122, 127, 166
- weighing 127, 141
- weight matrix 117-119, 124-126, 162, 172
- weight, in kohonen network 128
- weights 64, 116, 119, 122-123, 125
- weight 123
- welding 106
- widths 93
- width 98-99, 108, 195, 197
- window 54, 64, 92, 99, 108, 161
- workspace 179, 183
- workstation 198
- world, imaginary 27
- world, real 27
- world 56, 114, 159, 179
- wrist abduction 85
- wrist activity 91
- wrist adduction 85
- wrist, sperical 26
- wrist, spherical 181
- wrist 6, 82-83, 85, 87-99, 105
- writer, adult 5
- writers 22, 58, 76, 82-83, 105-106, 155, 158, 198, 202, 206
- writer 5-6, 18-19, 35, 38, 41, 49, 56, 58, 63-68, 70, 75-76, 83-84, 86, 101, 106-107, 167, 180, 191, 196, 198, 200-201, 204, 206
- write 39, 43, 56, 86, 88-89, 181, 198
- writing surface 6, 84
- writing, blindfolded 18
- writings 65
- writing 5-6, 17-18, 42-44, 53, 56, 64, 76, 81-90, 102-103, 105-106, 158, 164, 180, 193-194, 196, 200, 204-206
- written 35-36, 41, 44-46, 53, 70, 88, 91, 100-101, 192, 202, 204-206
- xor problem 119, 159
- xor 119
- zero crossings, current delay between 68
- zero crossings, target delay between 68
- zero crossings 38-39, 41, 44, 58, 60-61, 67
- zero-crossing time variability 43
- zeroes 167
- zeros 49, 125
- zone 134
- a,c,e,i,m,n,o,r,s,u,v,w,x,z 204
- b,d,h,k,l,t 204
- f 204
- g,j,p,q,y 204
- A 196
- H 68
- a,c,d,g,i,j,m,n,o,p,q,u,x 205
- a,b,c,d,e,f 167-168, 171
- a,c,e,i,m,n,o,r,s,u,v,w,x,z 64
- agee 43-46, 48
- agne 43-47
- ague 43-47, 49
- ag 43
- aquarel 202-203
- argumentatie 36
- a 10, 39, 44, 84, 102-104, 167, 169, 196, 202
- b,e,f,h,k,l,r,s,t,v,w 205
- b,v,w,u 205
- b,f,h,k,l 64
- b 204
- cl 192
- computer 42
- d,t 65
- d 169-170, 192
- elelele 58
- ellellell 58
- ellellle 158
- elle 53
- en 206
- er 206
- e 18, 39, 44-45, 62, 67, 75-76, 158, 167
- f,g,j,y 64
- f 167, 169
- g-* 46
- g-e 43, 45
- g-k 40
- g-n 43
- g-u 43
- gen 42
- g 39, 41-42, 45-46, 48, 101
- i 65, 67
- j 65
- k 66
- l 53, 158
- minimum 164
- m 62, 67, 76, 164, 192-193
- n.. 192
- n 76, 202
- or 206
- o 75
- p,q 65
- r 56
- s 56
- t 56, 66, 68, 196
- ui 18
- u 202
- w 164
- y 205
- A
braham 14, 24
Abramowitz 90, 109
Adams 5-6, 24, 152, 176
Agarwal 45, 47, 137, 150
Akazawa 131
Akkerman 110, 210-211
Albers 23, 27, 211
Allum 5, 24
Andreewsky 76
Antonj 132, 210
Asada 53, 76, 83, 109
Asanuma 116, 131, 149-150, 154, 176
Baier 82, 109
Ballard 21, 24, 116, 131, 135-136, 150, 157, 176
Barto 177
Bauer 176
Beech 25
Beek 14-16, 24, 86, 109
Bendat 24, 32-33, 46-47, 90-91, 109
Beni 24, 190
Bigland 116, 131
Bisiacchi 76
Bizzi 6, 9, 13, 24, 84, 109, 182, 190
Blinowska 137, 150
Boerhout 28
Bootsma 12, 24
Bozinovic 196, 210
Brady 110, 181, 190
Brault 75-76
Broadbent 22, 24
Brosch 176
Brown 36, 47
Bullock 152, 162, 176-177
Cannet 137, 150
Carpenter 157, 176
Chua 14, 26, 152, 177
Connor 158, 178
Coolen 125, 131, 136, 150, 156, 176, 182, 190
Crane 82, 109
Crick 116, 131, 149-150, 154, 176
Crossman 5, 24, 210
De Luca 5, 24, 137, 150, 157, 177
Deinet 82-84, 109
Denes 76
Denier van der Gon 6, 8, 24, 28, 51, 54, 65, 74-76
Desa 19, 24, 181, 190
Deschênes 76-77, 109-110, 190, 210-211
Dexel 99, 110, 198, 210
Di Marco 132, 210
Dijkstra 6, 8, 24
Dimond 5, 8, 24
Dooijes 17, 24, 38, 47, 51, 53, 56, 62, 76, 82, 86, 89, 106, 109
Dordoni 132, 210
Drexler 23, 27, 211
Eckhorn 157, 176
Edelman 106, 109, 115-117, 131-132
Ellis 10, 24, 52, 76
Elman 154, 177
Estes 154, 176
Fairbanks 4, 24
Fisher 177
Fitch 15, 27
Flash 7, 52, 76, 106, 109, 115, 131
Flude 10, 24
Fogelman-Soulié 27
Freeman 132, 157, 178
Freund 5, 24
Fujii 131
Furukawa 109
Gelatt 131
Gerritsen 23, 27, 211
Gibson 12-13, 24
Gielen 125, 131, 136, 150, 156, 176, 182, 190
Gisbergen 8, 25
Gold 38, 47, 62, 77
Goodman 25
Gottlieb 137, 150
Grimby 7, 25
Grossberg 127, 131, 152, 157, 162, 176
Grossman 154, 176
Hackwood 24, 190
Hale 82, 109
Hannerz 7, 25
Harley 23, 25
Harnad 115, 131
Hartmann 154, 176
Hayes 196, 210
Hedman 7, 25
Hinton 122, 124, 126, 131-132, 136-137, 139, 150, 153, 156, 176-177
Hoffman 204, 210
Hogan 13, 25, 82-85, 105, 109, 182, 190
Hogg 178, 211
Hollerbach 15, 19, 25, 49-52, 54, 76, 106, 109-110, 152, 176, 190
Hoosain 26-28, 31, 47, 50, 77, 110-111, 178, 211
Hopfield 123-126, 131-132, 153, 156, 176, 182
Houk 152, 177
Huberman 178, 211
Hull 25
Hulstijn 9, 15, 25, 61, 76, 105, 109, 152, 176
Hussong 109
Hylkema 9, 28, 178
Inbar 137, 150
Ivaldi 74-76, 84, 86, 110, 132, 182, 190
Janssen 99, 110, 198, 210
Jeffress 25
Johnson 110, 190
Jones 5, 25, 116, 132, 137, 150
Jordan 155, 157-158, 162-163, 176-177, 204, 210
Kanerva 149-150
Kanosue 116, 131
Kao 26-28, 31, 47, 50, 77, 85, 109-111, 178, 211
Kawato 107, 109
Kelso 7, 13-15, 25-27
Kennedy 27, 132, 210-211
Keuss 18, 26
Kirkpatrick 124-125, 131
Knoll 9, 27, 178
Kobayashi 82, 109
Kohonen 127-129, 131, 157, 177, 183-184, 186-188, 190, 195, 197, 202-203, 205, 210
Kondo 199, 210
Koster 51, 54, 77
Kraepelin 85, 109
Kretschmer 85, 110
Kruse 176
Lago 116, 132, 137, 150
Lamarche 51, 53, 77
Laming 7, 25
Lashley 6, 25
Lee 15, 25, 109
Linke 109
Lin 19, 25, 182, 190
Lippold 4, 25, 116, 131
Lorette 82, 110
Luh 19, 25, 182, 190
Maarse 17, 26, 33, 47, 49-52, 56, 62, 67, 76-77, 82, 85-86, 88, 92, 99, 110-111, 164, 178, 196-198, 200-201, 210-211
Maier 196, 208, 210
Mannaerts 18, 26
Marr 114, 132
Marsden 7, 26
Martin 176
Mason 83, 110, 190
McClelland 23, 26, 131-132, 136, 150, 154, 176-177
McIntosh 7, 26
Melton 176
Merton 7, 26
Meulenbroek 9, 28, 52, 76, 108, 178, 210
Milgram 137, 150
Mille 177
Mohler 7, 28
Monsell 9, 27, 178
Moore 177
Morasso 6, 9, 23-24, 26-27, 53, 56, 74-77, 84, 86, 109-110, 115, 129, 132, 182, 190, 202, 208, 210-211
Morton 7, 26
Mulder 110, 210-211
Mullins 27
Munk 176
Mussa 74-76, 84, 86, 110, 132, 182, 190
Niez 116, 132, 154, 177
Norman 154-155, 161-162, 177
O'Regan 25
Olson 7, 26
Ostrem 82, 109
Paganini 82, 109
Parker 14, 26, 152, 177
Paul 19, 26
Pellionisz 135, 150, 182, 191
Peretto 116, 132, 154, 177
Perkel 154, 164, 177-178
Pfeifer 27
Pick 2, 200, 210
Piersol 24, 32-33, 46-47, 90-91, 109
Plamondon 17, 26-27, 51, 53, 56, 75-77, 80, 82, 85, 87, 108-111, 177, 190, 198, 210-211
Polanyi 23, 26
Polit 9, 24, 84, 109
Poulin 76-77, 109-110, 190, 210-211
Pratt 158, 177
Rabiner 36, 38, 47, 62, 77
Rack 5, 13, 26, 105, 110
Raibert 52, 77
Reddish 15, 25
Redfearn 4, 26
Reeke 115-117, 132
Regan 32, 47
Reitboeck 176
Requin 24, 27, 47, 190
Rieger 109
Roberts 5, 26
Robinson 155, 177
Roebroek 8, 25
Rosenthal 5, 26
Roth 19, 24, 181, 190
Ruggiero 76, 132
Ruijgrok 125, 131
Rumelhart 23, 26, 122, 131-132, 136-137, 139, 150, 153-156, 161-162, 176-177
Sahar 19, 25
Saltzman 13-15, 26
Sanders 12, 15, 26, 113, 132
Schmidt 7, 20, 26
Schomaker 5, 10-11, 15, 18-19, 23, 26-27, 31, 33, 47, 49-51, 53, 72, 74, 76-77, 80, 82, 86, 88, 90, 92, 101, 106, 108, 110-111, 116, 137, 150-152, 155, 157, 177-179, 181, 183, 191, 194, 196, 200-201, 210-211
Schopman 131, 150, 190
Schreter 27
Schulman 177
Segundo 177
Sejnowski 124, 126, 131, 153, 176
Semenza 76
Shastri 155-156, 178, 204, 211
Shaw 14, 24
Shek 109
Simner 51, 76-77, 111, 177, 210
Singh 177
Sivak 7, 26
Sjouw 110, 210-211
Skarda 157, 178
Skrzypek 204, 210
Slotine 53, 76, 83, 109
Sloviter 158, 178
Smolensky 115-116, 132
Smyth 178
Southard 25
Srihari 196, 210
Steels 23, 27
Stegun 90, 109
Steinwachs 85, 111
Stein 123, 132
Stelmach 6, 15, 24, 27, 47, 105, 111, 190
Sternberg 9, 27, 113, 133, 152-153, 178
Stornetta 154, 178, 204, 211
Strackee 76
Sudhakar 45, 47
Suen 51, 76-77, 109-111, 177, 190, 210-211
Suhash 45, 47
Sutton 177
Suzuki 109
Tagliasco 76, 182, 190
Tam 154, 178
Tappert 196, 208, 211
Teder 109
Ten Hoopen 18, 26
Terzuolo 5, 26, 35, 47
Teulings 15, 23, 27, 32-33, 47, 49-52, 54, 56, 58, 65, 75-77, 82, 86, 105-106, 110-111, 164, 177-178, 194, 196-198, 200-204, 208, 210-211
Thomassen 15, 23, 26-27, 31-33, 47, 49-51, 54, 72, 74, 77, 86, 88, 92, 101, 106, 110-111, 177, 198, 200, 202, 210-211
Thuring 54, 65, 74-76
Torras i Genís 116, 133, 154, 157, 164, 173-174, 178
Tuller 15, 27
Turvey 15, 27
Van Boxtel 5, 27, 53, 77, 90, 111, 137, 150, 157, 178
Van der Plaats 10-11, 26
Van Doorn 116
Van Galen 9, 15, 25-28, 31, 33, 47, 50, 52, 61, 76-77, 105, 109-111, 116, 152, 173, 176, 178, 183, 191, 211
Van Opstal 8, 25
Vecchi 131
Verroust 137, 150
Viviani 35, 47
Von der Malsburg 154, 178
Von Hámos 4, 28
Vredenbregt 51, 54, 77
Wadman 6, 9, 28
Wakahara 211
Watrous 155-156, 178, 204, 211
Werbos 177
Wiener 2, 28
Williams 122, 132, 137, 139, 150, 153, 156, 177-178
Witteveen 59, 77
Wright 9, 27, 178
Wurtz 7, 28
Yoshida 131
Young 10, 24
Footnotes:
1 The name (KR) is rather strange since it seems to imply that the experimenter can be certain that the subject indeed has acquired knowledge upon the presentation of the feedback stimulus that is supposed to represent a response measure.
2 The notation will be used throughout the dissertation to refer to handwritten characters, i.e., "graphemes" or strings of graphemes.
3 Schomaker, L.R.B. (1988). Robotica en menselijke motoriek (Robotics and human motorics). In P.J.G. Keuss, G. Ten Hoopen & A.A.J. Mannaerts (Eds.), Psychonomische Publikaties: Motoriek (117 - 140). Amsterdam: Swets en Zeitlinger.
4 Published 1986 in: Kao, van Galen & Hoosain (Eds.) Graphonomics. pp. 225-238. Amsterdam: Elsevier. Supported by grants from NWO, project 560-259-020, and Esprit, project P419
5 Published 1989 in: R. Plamondon, C.Y. Suen, & M.L. Simner (Eds.), Computer Recognition and Human Production of Handwriting (pp. 153-177). Singapore: World Scientific. Supported by grants from NWO, project 560-259-020, and Esprit, project P419
6 Published in Biological Cybernetics, 63, 277-289, (1990). Supported by grants from NWO, project 560-259-020, Esprit, project P419 and the NIAS. ·Laboratoire Scribens, Département de Génie électrique, Ecole Polytechnique, Montréal, Canada
7 Since the actual area of the pen point is rarely included in the measurements, pen pressure will be referred to as pen force in this article.
8 In the Hopfield-network literature the weights are often called Jij instead of wij.
9 Movement segment: a limited-duration kinematic and/or kinetic, neural or myoelectric activation pattern, depending on the level of observation.
10 Hence the term Time Delay Neural Network (TDNN) that is used sometimes.
11 There are subtle distinctions between these concepts. "Planning" hierarchically precedes "Programming". Both concepts suffer from an algorithmic connotation, which in the case of motor control may be only justifiable for high-level (symbolic) task planning.
12 A version of the NETtalk model (pronouncing English words that are presented optically) by Sejnowski & Rosenberg (1986) displays a similar problem after reading the last input character.
13 Published 1990 in: Proceedings of the International Workshop on Frontiers in Handwriting Recognition (pp. 195-211). Montreal: CENPARMI Concordia. Supported by Esprit, project P419