Saboteurs
Multi-Agent Systems
Dyon Veldhuis, Eric Jansen and Eveline BroersApril 2012
Contents
Introduction
For the master course Multi-Agent Systems we created a program based on the game Saboteur. The aim of the program is to use beliefs to play the game. We have chosen the game Saboteur, because players do not know each others role in the game. They have to reason about who to believe and about what other players believe. Based on this, they have to reason about what cards to play, who to trust and who not to trust.
In this report we will discuss the structure of the game, the strategies the players can use, our implementation, what beliefs they use and the results.

The game
In the game Saboteur, dwarfs are building a path in a gold mine to find some gold. However, among them there are a few saboteurs! Will the normal dwarfs, the miners, reach the gold or will the saboteurs win the game?
The mine starts with a start card and three goal cards. The players have to create a path from the start card to the right goal card. Only one of the goal cards contains gold!
The rules
The game starts with assigning a role to every player: saboteur or miner. The players only know their own role. Furthermore, everyone will get six hand cards.
There are two types of cards one can hold: path cards and action cards. The action cards can be specified even further: block cards which can prevent another player from playing a path card; deblock cards to cancel a block card; rock-fall cards which give a player the opportunity to remove a path card (except the start and goal cards) from the maze on the table; map cards with which a player can inspect one of the goal cards.
On his turn, a player can choose from three possible actions: playing a path card, playing an action card, or pass. When a player cannot or does not want to play a card, he has to pass. This means that he has to put one of his hand cards face down on the discard pile. At the end of his turn, a player has to pick the top card off the deck into his hand (until the deck is empty).
A round ends when there is an uninterrupted path from the start card to the goal card with the gold. In this case, the miners win. When the players created a path from the start cards towards a wrong goal card, the game continues. A round can also end when the deck is used up and each player in turn has passed, making the saboteurs the winners. At the end of a round, all players reveal their real identity and the winners receive some gold. The player who has the most gold cards after three rounds wins the game.
The complete rules of Saboteur can be found here.
Simplifications of the game
For our implementation, we chose to make some simplifications to keep the project manageable. The main changes are described below.
In the real game, there are more dwarf cards then players. For example: if there are five players, 2 saboteur cards and 4 miner cards are used to define the roles. This means that the players do not know how many saboteurs there are in play. In our program we did not do this, so everyone knows for sure that there are two saboteurs. This also means that, over three rounds, the saboteurs have an advantage in our program, simply because there are more of them on average.
Instead of using three different types of (de)block cards, we only use one. This also means that a player can only have one block card in front of him. In the real game it is possible to have three different block cards in front of one player.
According to the rules, a path card has to be played next to another path card that is already on the table. This has to be done in such a way that the paths on all sides of the card match with the other cards in the maze. This means that you can play a card adjacent to another card without extending a path (you put two walls next to each other). In our program, this possibility is excluded because this does not happen a lot in a real game.
In our implementation it is only possible to play the game with five players (three miners and two saboteurs). In the real game the number of players can vary from three to ten.
At the end of each round, gold is distributed among the winners (miners or saboteurs). In the original game, not everyone will get the same amount of gold, but in our implementation they will. The players on the winning team all receive one piece of gold. This might change the tactic of a player, because in the real game, players might not only be concerned with letting their team win (miners of saboteurs), but also with their 'position' at the end of the game. When the miners win, the player who played the last card will receive most gold, followed by the person at his right, et cetera. In our implementation, everyone from the winning team receives the same amount of gold, so they are not concerned about which team player plays the last card.
Our board has borders: cards can be placed at most two tiles above the start card and below the goal cards, which means the length of the board is 13 tiles. The width of the board is 13 tiles as well. For an overview of the board, see Figure 2. In this board the cards look like squares. However, they are actually rectangular, like in the real games. This means they can only be placed in two orientations ('normal' or 180 degrees turned).
Implementation
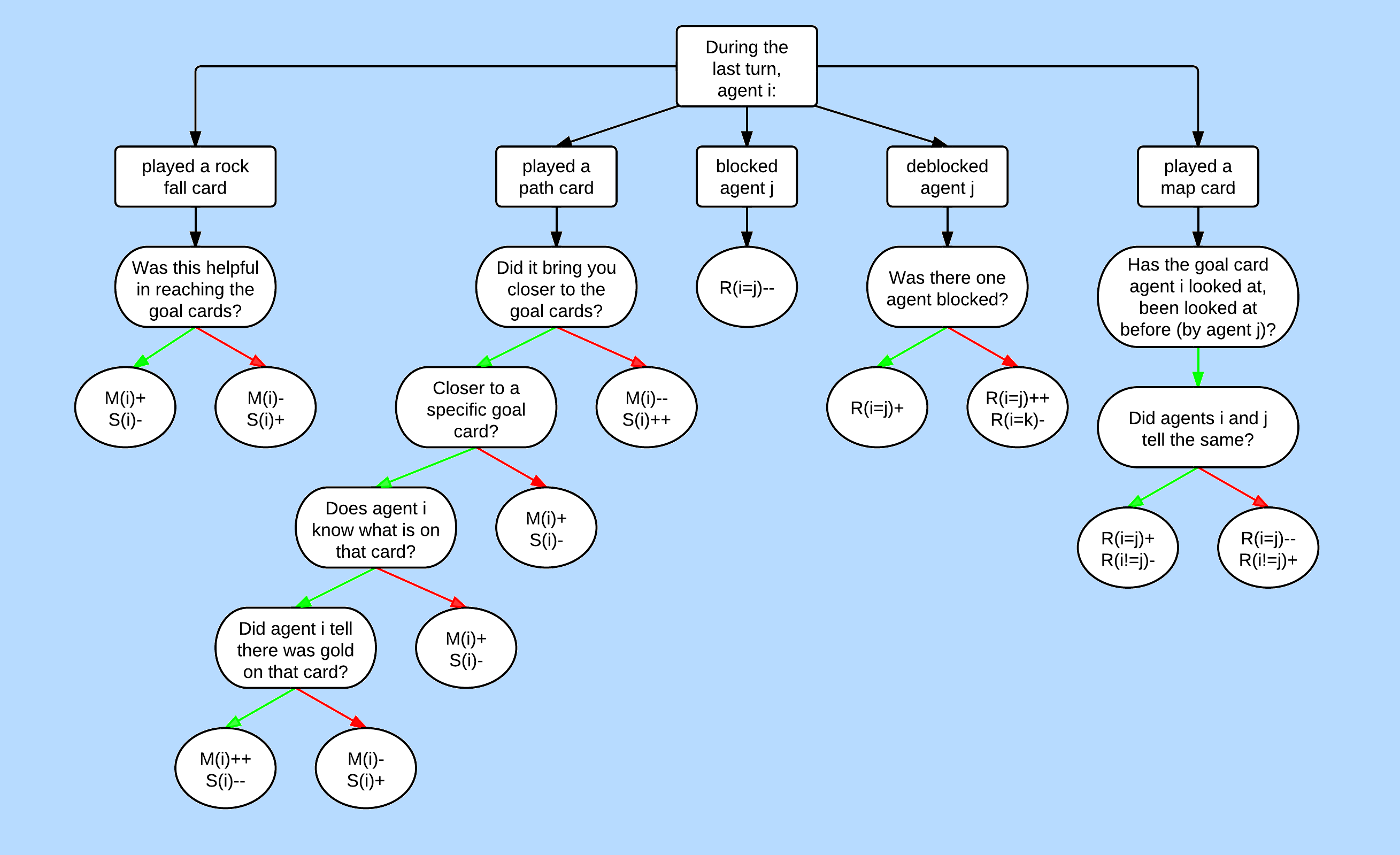
At every turn, a player has to decide what card to play. For this, we used an evaluation function for every type of card. We based this evaluation on the strategies following below. There are different evaluation functions for for saboteurs and miners. After each action, the beliefs of the agents can change. To update what the players think about each other, we used a Kripke model based on the flow chart presented at the end of this section.
Strategies for the saboteurs
Strategy 1: The saboteurs claim their role at the start of the game
If both saboteurs claim their role at the start of the game, it means that they start sabotaging immediately, but they don't explicitely tell this to the other players. This means that they do not have to do (semi-)good moves to keep their cover. Therefore, they can focus completely on sabotaging. A drawback of this strategy is that the miners know who they have to block. Therefore, it is likely that most of the time the saboteurs are unable to play path cards, because they are blocked. In those situations, however, they can block miners, destroy some pathways and lie about what is underneath a goal card.
Main actions: destroy paths, throw away good path cards, play path cards that close paths, direct paths in wrong direction, block miners, lie about the goal cards, throw away good path cards.
Strategy 2: The saboteurs don't claim their role at the start of the game
In this way it is hard for the miners to figure out who not to believe. Also, the saboteurs have to sabotage in subtle ways. This sounds less effective than the previous two strategies, but the advantage is that the miners will block them less. Therefore, the saboteurs might have more influence on the path, because they can actually play path cards. When the miners suspect a saboteur, it might be wise for that saboteur to drop its cover and start playing like a saboteur. They are already blocking him anyway and he cannot block the miners as much as he wants to when he stays under cover. More about this at the end of Kripke model.
Main actions (while still acting like a miner): throw away good path cards, blocking miners, lie about the goal cards.
Strategy for the miners
The miners want to get to the gold as fast as possible and they want to discover who the saboteurs are. To accomplish the first goal, the miners try to create the shortest possible path towards the gold. However, at the start of the game it is not known where the gold is. For a miner it is best to look at the goal cards itself, because he does not always know who to trust. Unfortunately, this is not always possible. Therefore, a miner has to combine its own beliefs with the things the other players tell him, to verify their story. A miner has to think about the actions other players do too, to see if they behave suspicious. In this way they could accomplish their second goal: reveal the saboteurs.
When a miner does get the chance to look at a goal card, he should tell the truth about it, because his goal is to get to the gold. Therefore, the miners need to know in which direction their path should go.
When a miner thinks another player is behaving suspicious (e.g. creating an inefficient path, lying about the goal cards or blocking players that are not suspicious), he can block this player. When someone is blocked, but the miners thinks that the blocked player is not behaving like a saboteur, he should unblock this person.
Main actions: creating shortest path towards gold, get certainty about the location of the gold, block saboteurs.
Play (de)block cards
If a player wants to play a block or deblock card, he has to decide where to play it. For this, he has to use his Kripke model to determine if there is someone who he trusts. When a player is blocked, he will deblock himself before deblocking someone else. If not blocked, a miner might deblock the player who is least suspicious. A saboteur will never deblock someone else, he focusses more on sabotaging the miners. When a player wants to block someone, he will select the most suspicious player that is not blocked yet.
Kripke model
The agents need to reason about the roles the other agents have. To do this, they use a so called Kripke Model in the KD45(m)-system. Every agent has its own model and it consists of ten states, one for every possible distribution of the role cards. The model starts with a relation from every state to every other state, for every agent, because all agents consider all states to be possible at this point. After the role cards have been dealt, the agent removes his own relations towards the states in which his role is not correct.
During the game, an agent John updates his own relations and the relations of the other agents within his model. This happens in the following way: John evaluates the action another agent i takes. This can increase its beliefs in states where agent i is a saboteur or where i is a miner. When the belief in some state is below a certain threshold, John his relations to that state will be removed. The relations will be added when the belief has reached the threshold again. The implementation of how an action is evaluated, is based on the flow chart in Figure 1. This is used to update the Kripke model after each turn. The update of a disbelief in a state is 1.5 times stronger than the update of a belief in a state. This is done to make sure that agents dismiss states after a while. John also reasons about how the beliefs of other agents change after agent i has taken an action. He assumes that the other agents reason in the same way as he does.
When John is a miner, he uses the relations of other agents in his model to update his own beliefs. He selects the player he trusts most and enough (that player should be a miner in more than one state and a saboteur in at most one state that John believes in). Then John looks at the relations that the selected agent has in his model, and slightly changes his own beliefs towards the beliefs of that other agent.
When John is a saboteur, he uses the relations of other agents to decide when to claim his role. When he believes most other agents believe that he is a saboteur, he will stop faking that he is a miner. He will conclude that this is the case in the following way. After the role cards are dealt, John will remove all relations of other agents to states where those other agents are saboteurs, because everybody is or pretends to be a miner. This means that in John his model, every other agent believes in six states, and in three of those states John is a saboteur. For John to believe that someone finds him suspicous, that other player needs to believe in at most one state where John is a miner and in equal or more states where he is a saboteur. When there are two such agents, John will become an explicit saboteur player. Another reason to become explicit is when the miners could reach the goal within two steps. When a saboteur is not pretending to be a miner (any more), his evaluation functions for the different cards change.
 |
Experiments
We modeled the whole game, which consists of three rounds. The winner is the agent who has most gold at the end of those rounds. However, the roles of the agents are different per round, so this is not very interesting for our project. Therefore, in gathering results, we looked at the different rounds in stead of the different games.
Experimental setup
We tested different configurations of the program.
- We varied the strength with which the disbelief in states increases: in the normal settings it is 1.5 times stronger than the update for believing in a state. In the second configuration, it is 5 times stronger than the update for believing in a state. This was done to see whether the number of states that an agent believes at the end of the game would decrease.
- We have two options for the beliefs used: beliefs with a depth of one and beliefs with a depth of two. Without beliefs of depth two, miners don't take into account what they believe others believe to update their own beliefs. A saboteur only becomes explicit when the miners are close to the goal and not when he thinks that other agents believe that he is a saboteur.
- Saboteurs can have different strategies: in one configuration they play like a saboteur from the start. In the second they use the tactic described above: a saboteur becomes explicit when the miners are close to the goal or when he believes he is suspected to be a saboteur. In the last configuration, they never become explicit.
Results
- Most of the time, the saboteurs win.
- After almost every round, all agents believe (at least) in the state that is actually true.
- When the change in belief was stronger than in the original settings, agents believed in less states at the end of the game for all configurations.
- In the two configurations where the saboteurs (can) become explicit, there was no change in result when agents did or did not use beliefs of depth two.
- There were no striking differences between games where the saboteurs were explicit from the start and games where they become explicit when 'necessary'.
- When the saboteurs never become explicit, the results are different. The miners win virtually every time when the agents use belief of depth two. When no depth two beliefs are used, the saboteurs win sporadically. Another difference is that there are more occurences where an agent does not believe in the state that is actually true. They don't seem to have a clue what is really going on. Overall, this does not aid the saboteurs in our implementation of the game, because the players are rather simple. However, it is interesting to see that playing under cover whilst not really aiding the overall goal of reaching the gold, can in fact be positive for the saboteurs because it causes confusion. This tactic might aid a more complex player.
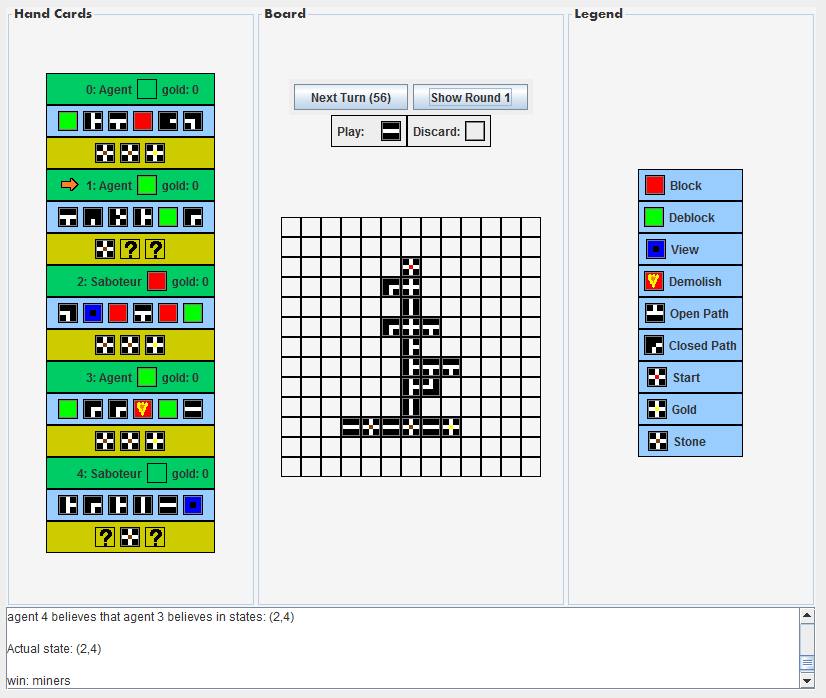
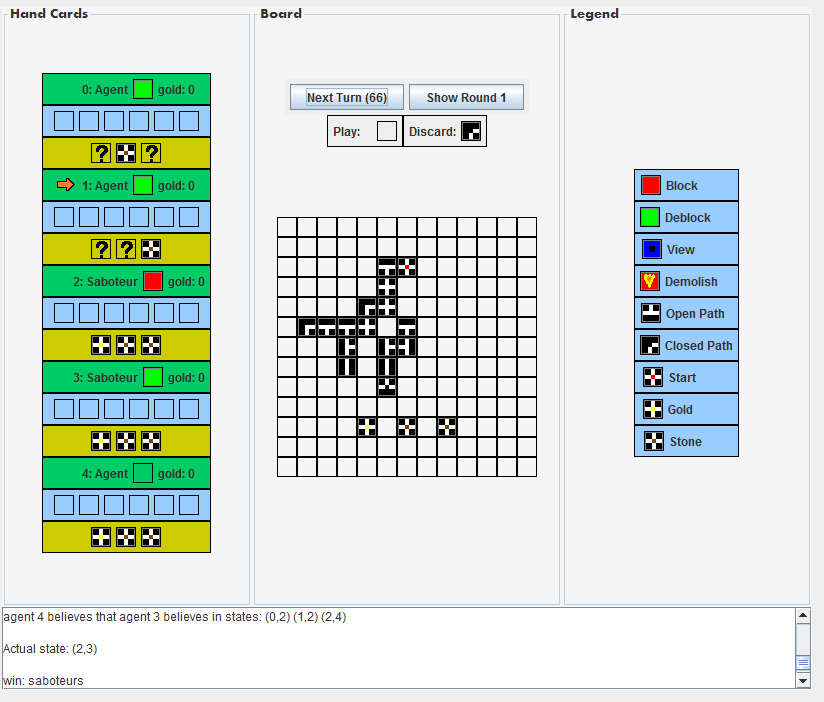
In Figure 2 and Figure 3 you can see the end board of two games.
 |
 |
Conclusions
We have created a program that simulates the game Saboteur where the players use beliefs to play it. Altough there is no real advantage in belief with depth two in our implementation, we did find differences in beliefs, especially when the saboteurs try to remain undiscovered. It would be interesting to see what more complex agents would do with the beliefs gathered in our system. We don't think adding deeper beliefs would aid the performance of the agents, since beliefs of depth two did not seem to help much.
The simplifications we made to the game, seem to be benificial towards the saboteurs. They can only be blocked once and on beforehand it is already known that there will be two of them as opposed to the possibility of having either one or two saboteurs.